Weekend Mathematics/問題/問題36
36.まきの問題
ひとりの女の人が住んでいます。
仮に三木さんと呼ぶことにしましょう。
三木さんが台所用の共同スト−ブに自分のまきを3本入れました。
もう一人の女の人の五木さんは5本入れました。
別の住人である木無君は、自分のまきがありません。
でも、共同の火で昼食をつくる許しをえました。
その出費のつぐないとして、8コペイカを2人の隣人に払いました。
ふたりの婦人はこれをどのように分けたらよいでしょうか。
数学のはなし
ペレリマン
東京図書
(ペンネ−ム:青光)
3人で薪を8本使ったので、一人あたり 8/3 本の薪を使ったと考えます。
すると、三木さんが木無君に分けてあげた薪は 9/3 - 8/3 = 1/3 となります。
同様に考えると、五木さんが木無君に分けてあげた薪は 15/3 - 8/3 = 7/3 となります。
よって、木無君に分けた薪の比は、三木さんと五木さんで 1 : 7 となります。
以上の理由より 1 : 7 で分けるべきだと思います。
この問題は見た瞬間に「3:5に決まってるじゃん。」とか思ったの
ですが、そんな簡単なのかな?と考えてみたら、意外な答えでびっくりです。

(ペンネ−ム:kiyo)
(3+5)÷3=8/3 一人あたりの必要なまきの本数。
三木さんと五木さんの余分なまきの本数。
3−8/3=1/3
5−8/3=7/3
(1/3):(7/3)=1:7
三木さん 1コペイカ
五木さん 7コペイカに分ける。
これも一つの考え方だと思います。

(ペンネ−ム:不信邪(プーシンシェ))
8コペイカが3人のそれぞれの負担に適切なのでしょうから、
8本/3=8/3本=8コペイカ
三木さんは8/3本負担すべきところを3本出していますので、(3−8/3)本出しすぎています。
五木さんは、8/3本負担すべきところを5本出していますので、(5−8/3)本出しすぎています。
それぞれを返却するのですから、
三木さんには、(3−8/3)X3=1コペイカ
五木さんには、(5−8/3)X3=7コペイカ
となります。

(ペンネ−ム:ちゃめ)
三人が使う割合は同じである、すなわち、木無君はまき(8/3)本の代価として8
コペイカ支払ったものと考えます。
すると、まき1本の値段は3コペイカ。
まき3本を提供した三木さんの過払い分は、
3×3−8=1(コペイカ)
まき5本を提供した五木さんの過払いぶんは、
3×5−8=7(コペイカ)となる。
したがって、
三木さん1コペイカ、五木さん7コペイカと分ければよい。

(ペンネ−ム:sambaGREEN)
まきは全部で8本だから,ひとりあたりの使用量は 8/3
三木さんが木無さんに提供したのは 3−8/3=1/3
五木さんが木無さんに提供したのは 5−8/3=7/3
したがって,三木さんが1コペイカ,五木さんが7コペイカ受け取ればよい。
【コメント】
3人で会社を作るのに,2人が異なった広さの土地を出資し,1人は土地を持ってないので現金を出資,
そして,・・・というような類似問題を解いた記憶があります。

(ペンネ−ム:もこりろ)
まきは全部で8本。従って一人分の料理には
8/3本のまきが必要
| 三木 | 五木 | 木無 | |
|---|---|---|---|
| 自分のまき | 9/3 | 15/3 | 0 |
| 必要なまき | 8/3 | 8/3 | 8/3 |
| 残 り | 1/3 | 7/3 | −8/3 |

(ペンネ−ム:少年H)
木無君の出費8コペイカが割り勘にした時の一人当たりの出費であるから、3人の出
費のトータルは、8コペイカ×3=24コペイカである。
この24コペイカがまき8本の値段と同じだからまき1本あたりの値段は3コペイ
カとなる。
よって
三木さんの当初の出費は3本×3コペイカ=9コペイカであるから9−8=1コペ
イカをもらい、
五木さんは当初の出費が5本×3コペイカ=15コペイカであるから15−8=7
コペイカをもらう

(ペンネ−ム:ふじけん)
新しく、まき1本分の火の使用量を1バームとします。
すると、
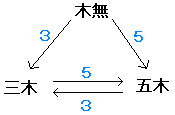
木無君は三木さんに3バーム、五木さんに5バームを、
三木さんは五木さんに5バームを、
五木さんは三木さんに3バームを
払わなくてはなりません。
そうすると、
木無君は8バームを払い、
三木さんは1バームを受け取り、
五木さんは7バームを受け取ることになります。
ここで、木無君は8コペイカを二人に払ったので
1バーム=1コペイカ
となるので、三木さんは1コペイカ、五木さんは7コペイカ受け取るべきである。

(ペンネ−ム:浜田 明巳)
問題の条件が今一はっきりしないので,こちらで勝手に次の2つの仮定をさせてもらいます.
仮定その1.三木さんは五木さんに対して,「まきを5本も入れる必要はなかったのよ,
3本で十分だったのよ」等とけんかをふっかけない.
仮定その2.共同の火で使うまきは,火を使う時間に関係なく,あるいは料理の量に関係なく,
使う人が平等に分担します.
つまり火は誰かが独占してはいけないものであり,
誰かが「ちょっとしか使わないからちょっとしかまきを出さない」と言わない,という事です.
この仮定はそんなに非常識なものではないでしょう.では解きます.
木無君は,まき8本の1/3に対して8コペイカ払った訳ですから,
まき8/3本の値段が8コペイカ
すなわち,
まき1本の値段が3コペイカ
となります.
木無君の8コペイカは,三木さんと五木さんに公平に4コペイカずつ分けるべきでしょう.
しかし三木さんと五木さんは本来4本ずつまきを公平に出すべきだったのですが,
五木さんは三木さんの分の1本をよけいに出しました.
したがって三木さんは五木さんにまき1本分の3コペイカを払うべきです.
つまり木無君の8コペイカは,
三木さんに1コペイカ(4−3),五木さんに7コペイカ(4+3)
と分けるべきなのです.

(ペンネ−ム:Chee)
「共同ストーブ」なので、まきの恩恵(火)は平等に利用できるとします。
8本分の火を3人で平等に利用するのだから、木無君は 8/3 本分の火を使ったこと
になります。
さて、木無君が使ったの 8/3 本のまきの出所は?というのが問題です。
ところで、彼女たちも同様に 8/3 本分の火を利用しているので..
三木さんは、3 - 8/3 = 1/3 本
五木さんは、5 - 8/3 = 7/3 本
を、木無君に提供したことになります。
その報酬が8コペイカということは、提供したまきの比率(1:7)から
三木さんが、1コペイカ
五木さんが、7コペイカ
もらえば良いことになります。
# まき1本は3コペイカなんですね。
[気になりました..]
彼女たちの一方が、もう一方の2倍より多くのまきを出してしまった時は、木無君は
いくら出せば良いのでしょうか?
解答と同じ考えだと、少なく出した方も恵んでもらったことになりますから、この子
もいくらか出すことになるでしょう。
しかし、考え様によっては、一人分としては十分な量なのかもしれません。
つまり、多く出した方は、出しすぎたのでしょう。
この場合は、(木無君に恵んだのは多く出した人だけなので)お金はみんなもらえる
でしょうが、損します。
もっと考えると、彼女たちは、3人では使い切れないぐらいのまきを出してるかもし
れません。
その分のお金を木無君が出すのは、ワリに合いません。
逆に、3人で使うには少なすぎる量ということも考えられます。
この場合だと、お金をもらうより、自分の必要な分までは使って欲しくないと思うの
が人情でしょう。
つまり、「平等」というのは平和的な表現ですが、この問題は、
「余計なおせっかいによる、余ってしまったまき」や
「自分勝手な行為による、足りなくなったまき」
までも平等にしようという、争いのタネが潜んでいます。
数学的ではありませんが、日常的な平等を考えると、単純な計算では済みそうもあり
ません。
こう考えると、この問題が成り立つには、
「出したまきは、過不足なくちょうど3人分の量」
という条件が、(暗黙の内に)必要なのでしょう。

(ペンネ−ム:クリーム)
三人の人がそれぞれまきやお金を出資して共同の火を起こした
わけですから、三人の出資が等しくなるように8コペイカの分け方を
決めるのが良いと思われます。
三木さんが受け取る分を a コベイカ、五木さんが受け取る分を
b コベイカとしましょう。
a+b = 8 ********(1)
また、1コペイカがまきα本と等価であるとしましょう。
すると、三木さんはまき三本を提供して、a コベイカを受け取るので
出資の合計はまきの本数に換算して、
3 - aα 本 **********(2)
同様に、五木さんの出資の合計は
5 - bα 本 ***********(3)
また、木無君の出資の合計は
8α 本 ***************(4)
となる。式(2)(3)(4)がすべて等しいとおいた連立方程式と式(1)との連立方程式を
解くと、α=1/3, a=1, b=7 を得る。
したがって、三木さんが1 コペイカ、五木さんが7コベイカ受け取るのがよいと思われます。
この解答にはかなり不満です。というのは、1コベイカがまき何本と等価であるか
(つまりαの値)が、この問題の連立方程式から自動的に決まってしまっています
が、それは不自然で、αの値はこの問題とは独立に決まっているものだと思うからです。

(ペンネ−ム:夜ふかしのつらいおじさん)
解答1
木無さんは、三木さんに1コペイカ、五木さんに7コペイカ支払うのが妥当。
一人8/3本ずつまきを出し合えば金のやりとりの必要はない。
三木さんは 3−8/3=1/3本、五木さんは5−8/3=7/3本余分に出
しているのでその余分に対して木無さんは代金を支払う。
(三木さんに3コペイカ、五木さんに5コペイカ支払うと、まき8本全部木無し
さんの権利となり二人は相応の代金を支払わねばならない)
解答2
出したまきの本数に対応して、三木さんに3コペイカ、五木さんに5コペイカ。
(金の問題は感情的なトラブルをおこしやすいので二人が問題を感じないなら。
木無さんにとっては8コペイカの出資は変わらないので二人の納得の問題である)

| ふじけん | 少年H | sambaGREEN |
| 浜田 明巳 | 夜ふかしのつらいおじさん | kiyo |
| Chee | もこりろ | クリーム |
| 青光 | 不信邪(プーシンシェ) | ちゃめ |

日常でもこういった場面はあり得るのではないかと思います。
ほとんどの場合、青光さんの解答・その1にあるように、
「3:5に決まってるじゃん。」ですよね?
でももうおわかりですよね?
あなたが五木さんだったら、それでは損してしまいます・・・。
しかしながら
コロキウム室NO.677のIdaho Potatoさんはじめ、
何人かの方が疑問を持たれているように「社会的」問題と考えると、また違った側面がでてきます。
そういう意味では、
夜ふかしのつらいおじさんの解答・その12の「解答2」が平和的かもしれません。
関連した話題が、コロキウム室 NO.677、 コロキウム室 NO.715、 コロキウム室 NO.716にあります。
さて分配と言えば、この話を思い出します。「ラクダの分配」です。
「数学のたのしさ」 矢野健太郎著 新潮文庫より
むかし、アラビアの商人が、ラクダを17頭持っていました。 アラビアの商人にとっては、砂漠を越えて遠い国へ商売に行く必要がありましたので、 そのため、ラクダはなくてはならぬもので、それを17頭も持っているというのは、 相当な財産を持っていることになります。
さてこの商人が、年をとって死のうとするときに、自分の3人のこどもをまくらもとへ呼んで、つぎのような遺言をしました。
「自分は17頭のラクダを持っているが、そのうちの1/2は長男に、1/3は次男に、1/9は三男にやりたいと思う。 3人はそれぞれのラクダを持ってしっかり商売ををやり、いつまでも仲良く暮らすようにしなさい。」
こういって商人は死んでしまいました。 そこで3人の子どもは、おとうさんのいうとおりにラクダを分けようとしたのですが、 これがなかなかうまくいきません。
ラクダは17頭いるのですから、長男がその1/2をとろうと思えば、17の1/2で8頭と半分ということになりますが、 まさかラクダを半分にして殺してしまったのでは、なんの役にも立ちません。
次男も三男も同じ理由で困ってしまい、どうしても、おとうさんのいうとおりにラクダを分けることができず、 すっかり困ってしまいました。
その話しを聞いたある年寄りが、 「よし、それならわしがうまく分けてやろう。」 といって、自分のラクダを1頭つれて、この3人の兄弟のところへやってきました。
この年寄りは、そこにいる17頭のラクダに自分のラクダを加えましたので、ラクダの数は18頭になりました。 そこでその年寄りは3人の兄弟に次のように言いました。
「長男は、1/2というのだから、18頭の1/2の9頭をとりなさい。 次男は1/3というのだから、18頭の1/3の6頭をとりなさい。 三男は1/9というのだから、18頭の1/9の2頭をとりなさい。
これで3人とも、おとうさんのいったとおりのラクダをもらったのだから、満足だろう、 これからは仲良く暮らすのですよ。」
さてこの年寄りは。長男に9頭、次男に6頭、三男に2頭のラクダ、つごう17頭のラクダをわたしたあと、 残った自分のラクダを1頭つれて帰ってしまいました。
みんなは、この年寄りの頭のよいのにほとほと感心しました。
さてこの話には続きがあります。再び「数学のたのしさ」より
それから数年たって、またラクダを11頭もっているある商人が、死ぬときにその3人の子どもに 次のような遺言をしました。
「自分は11頭のラクダを持っているが、その1/2を長男に、その1/3を次男に、その1/6を三男に やる。」
ところがこのときも、3人の子どもは、11頭のラクダをおとうさんのいうとおり分けることができずに 困ってしまいました。
そのとき、前の話を思い出したある男が、
「よし、自分がうまくわけてやろう。」
といって、自分のラクダを1頭つれて、この3人のところへきました。
ラクダは11頭と1頭で全部で12頭になりましたので、この人は次のように言いました。
「長男は、1/2というのだから、12頭の1/2の6頭をとりなさい。 次男は1/3というのだから、12頭の1/3の4頭をとりなさい。 三男は1/6というのだから、12頭の1/6の2頭をとりなさい。
さて、この人は、長男に6頭、次男に4頭、三男に2頭と全部で12頭のラクダを やってしまったので、なんと自分のラクダを1頭損してしまいました。
今回は、11という数が2でも3でも6でも割りきれないところにのみ問題があったわけです。
1を加えて12にすれば、2でも3でも6でも割り切れるので解決です。
ところが、今回は 1/2+1/3+1/6=1 になっていますから、
それに気がつかない男は加えた分のラクダを損してしまったわけです。
 E-mail
E-mail
 戻る
戻る