Weekend Mathematics／問題／問題28

２８．道路工事の問題

どこの国でもお役人は人の迷惑など考えずに道路工事をやるのが大好きです。
ガンレ−部長も例外ではありません。 予算をできるだけパ−ッと使うのが趣味ですから、なるべくたくさんの 場所で工事をやりたいと考えました。 でも、同じ町ですから、たとえ遠回りをしても、行きたい所へ行けないようでは困ります。
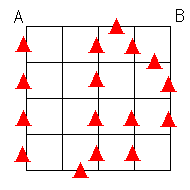
ガンレ−部長が最初に考えた案では、１６ヶ所で工事をします。 しかし、これではＡ点からＢ点に行くことができません。 市民から文句がでるのは必至です。

各頂点間の行き来を確保して できるだけたくさん工事するとしたら、 最大何ヶ所工事できるでしょうか？

解答・その１

（ペンネ−ム：かに）

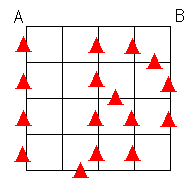
答えは 16 ヶ所でしょうか。
添付ファイルで題意を満たす工事箇所を示します。

解答・その２

（ペンネ−ム：数楽者）

答 １６本

解説 頂点は２５あるので、工事できない場所の最少数は２４である。
頂点を結ぶ線分は４０なので、工事できる場所の最大数は４０−２４＝１６となる。
グラフ理論で言う木(tree)になります。

解答・その３

（ペンネ−ム：Idaho Potato）

答えは「16ヶ所」です。
このことを示すには、次の2つのことを確かめなければなりません。

(1) 17ヶ所以上は不可能である。

オイラーの多面体の公式(平面の場合)を用います。
まず、問題の街路において、 f: 面の数, e: 辺の数, v: 頂点の数 とすると、

f - e + v = 1

が成り立ちます。
この街路から、「連結性」および「頂点の数」を保ったまま、辺を取り除き、 結果的に辺の数が e' 、面の数が f' になったとすると、そのとき

f' - e' + v = 1

が成り立っています。
これら2つの式から v を消去して、適当に移項すると、

e - e' = f - f'

が得られます。
問題の街路では、f = 16 で、かつ f' ≧ 0 ですから、 取り除かれる辺の数 e - e' の上限は 16 となります。

(2) 16ヶ所は可能である。

これは、実際にそういう状態の例を作ってみせれば十分です。
たとえば、すべての南北の道路と 1本の東西の道路を保って、残りをすべて工事すればOKです。
このとき、工事区間を除いた街路には、「面」は存在しません。

どんな街路(=連結な平面グラフ)についても、 「連結性」と「頂点の数」を保ったまま、 面の数と同数の辺を取り除くことができる

解答・その４

（ペンネ−ム：マサボー）
まず、全ての格子点を結ぶ最少の線の数を考える。 道を最少にするためには、各格子点とも入る道と出る道の2本とし、 最後の点だけ入る道のみとする。 このように考えると、最後の一点を除き各格子点が一本の道を持て ば格子（正確には格子ではないけど）が作れるので （簡単にはマッチ棒を考え、マッチの頭を格子点、棒を道として格子をつくる）、 全格子点の数から１引いた数が必要な道の数となる。 よって辺 n の格子点の数は(n+1)²より、 必要な道は n²+2nとなる。

問題は辺 4の場合なので、4²+2x4 = 24 の道が必要で、 道の数は40より40-24 = 16
最高で16本の道路で工事ができる。

「Idaho Potato」さんが指摘してくださった、 オイラーの多面体の定理を確認しましょう。
一般に平面上や空間の中の図形Ｋが三角形分割されているとき、 面の数ｆと、辺の数ｅと、頂点の数ｖを数えて
χ（Ｋ）＝ｆ−ｅ＋ｖ
とおいて、χ（Ｋ）をオイラ−数といいます。
χ（多角形）＝１というのが、オイラーの多面体の定理です。

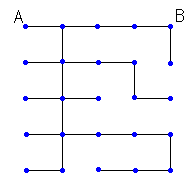
右の図は、「かに」さんが示してくださった例の通りに道路を切断した図です。
道路工事をするということは、辺を１つ減らすと同時に面を１つ減らすことになります。 このとき、頂点の数は変わりませんからオイラ−数は変化しません。
最大何カ所工事ができるのかと問われれば、面の数だけということになるでしょう。
閉じた面をこわすように１ヶ所ずつ辺を切っていって、面がなくなれば終わりです。
従って、この場合は１６ヶ所ということになります。

この閉じた面を含まない線系を樹形と呼びますが、 「マサボ−」さんのおっしゃる通り、
(頂点の数)＝(辺の数)＋１となっています。
これがオイラーの多面体の定理χ（多角形）＝１たるゆえんです。

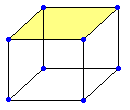
では、多面体ではどうでしょう？
まず、どこか１つ面を取り除きます。
そうしますとそこに穴があきますから、面、辺、頂点の連結を変えずに 平面に押し広げることができます。
たとえば右の立方体では、上面を取り除いて広げると、次の図のようになります。

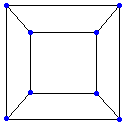
ここからは平面ですから、先ほどと同じです。
従って多面体では、工事できる最大数は(面の数)−１ということになります。
また、このことからオイラ−の多面体の定理χ（多面体）＝２ も理解できると思います。

戻る