Weekend Mathematics/コロキウム室/1998.7〜12/NO.29
コロキウム室
NO.224 12/8 Junko パスカルの三角形(2)
NO.218にあるパスカルの三角形を使って、
倍数の色塗りをしてみました。
やってみると、いろいろとおもしろいことに気づきます。
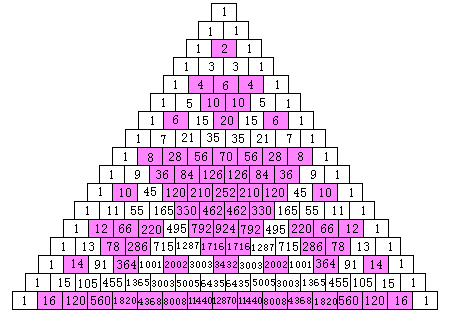
2の倍数
まず目につくのが逆三角形ですね。
2の倍数と2の倍数を足すと、それも2の倍数ですからね。
(これは2に限ったことではありません。)
これを偶数、奇数の勢力図とみると、なんだかおもしろいと思いませんか?
例えば8の段をみると、ほとんど偶数(2の倍数)
ということで塗られていますが、
両端に奇数である1がいるので、
まわりから序々に浸食されていくのですね。
でも奇数は2つくっつくと次の段でまた偶数になってしまうので、
完全に奇数になるのは大変です。
15の段でやっと偶数を排除できました。
でも当然、次の段は偶数だらけ・・・。
次ぎに奇数だらけになるのは25−1=31でしょうか?
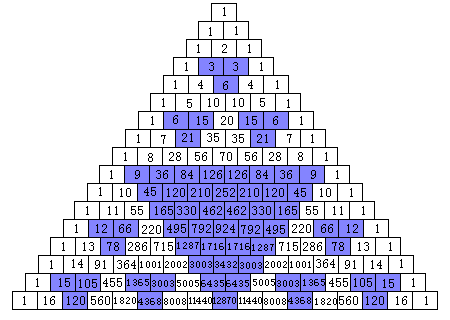
3の倍数
32=9のところには
大きな逆三角形ができています。
3個ずつの三角形が多いのは偶然でしょうか?
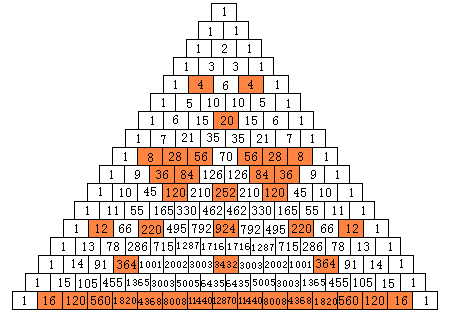
4の倍数
こうしてみると、4の倍数は以外と少ないなという印象を受けますが、
42=16から大きな三角形ができそうですね。
16の段で終わっているのが残念。(もう少し根性を出して作れば良かったかなあ・・・)

5の倍数
この色塗りをしてみて、思ったことは、
素数(約数が1と自分以外にないもの)の倍数の方が
きれい(というか明解)だということです。
5の倍数を見ると、5の段から1つ、10の段から2つ、
15の段から3つ・・・・というように三角形ができています。
そしてそれ以外のところに
ひょっこり5の倍数があるなどということはないのです。
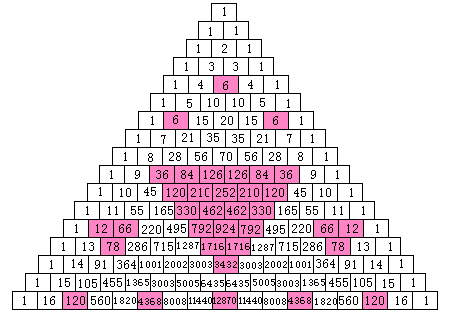
6の倍数
素数でないものを合成数といいます。
先ほどの5の場合と比較すると、かなり複雑です。
6=2×3と素因数分解できますから、
当然2の倍数の図と3の倍数の図の重なったところになるわけです。

7の倍数
7も立派な(?)素数です。
塗られ方がクリア−ですよね。
ところで、nが素数のとき、
nの段は両端の1を除くとすべて塗られるということがいえるようです。
ですから、そこから逆算角形ができているわけです。
6の倍数の表を見直していただければわかりますが、
これはnが素数でないといえません。
「nが素数のとき、nCk(1≦k≦n−1)は
必ず、nで割り切れる。」
証明
ところが、nは素数だから1,2,3,・・・k-1,k(k<n)のいずれもnを割りきらない。
従って、nCkは必ずnの倍数となる。
パスカルの三角形を見ていると、
他にもいろいろな秘密が隠されているようですね。

NO.225 12/10 Junko コマの動き方(2)
「コマの動き方」の方ですが、これはフィボナッチ数列の2次元への拡張とも考えられますね。
座標(m,n)までたどり着く経路の総数をS(m,n)とすると、
漸化式S(m,n)=S(m,n−1)+S(m−1,n−1)+S(m−1,n)
が成立するのではないかと思います。
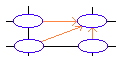
上の図のように、この駒は右、上、斜め上と3通りの方法で
1ますづつ動くことができるからです。
つまり自分から見て左、左下、下の3つのマスの和を計算していれればいいことになります。
それに従って計算してみました。
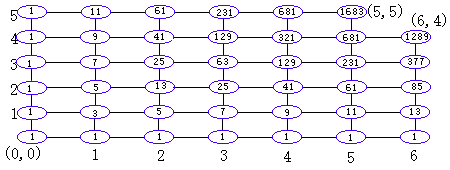
問1 一番右上のますの座標が(5、5)のときの経路は1683通り
問2 一番右上のますの座標が(6、4)のときの経路は1289通りとなります。

NO.226 12/10 水の流れ コマの動き方(3)


NO.227 12/11 Miyazo 円錐の体積(1)
今算数の勉強で「立体に体積」という単元をしていますが、
その中で角錐、円錐の体積についての学習をしました。
公式としては
底面積×高さ÷3(×1/3)ということで子どもたちに指導していますが、
この1/3ということに疑問が生じました。
どうして1/3となるのでしょうか?
「東京書籍」の教科書では、
水を使って1/3ということを視覚的に指導していますが、
子どもたちにはどうして1/3になるのか?
という疑問が残っているようです。
小学校の段階ではそこまで指導しなくても良い扱いとなっていますが・・・。

NO.228 12/12 水の流れ 円錐の体積(2)
この質問を受けたとき、真っ先に浮かんだ本が次ぎのものです。
答えになるものがでてきます。
BLUE BACKS マンガ 微積分入門
講談社 岡部恒治 著
お持ちでなければ、購入してみてください。
きっと、目からうろこがはがれます。
ここで、簡単に説明します。
三角形の面積Sは 底辺=a,高さ=h とすると
S=(高さ)×(底辺)÷2
この底辺は ある底図形の量(この場合は直線)、
2は 2次元 の2 です。
3次元のすい体の体積Vは(円錐、四角錐、三角錐、多角錐 ・・・)
底面積=S、高さ=h とすると、
V=(高さ)×(底面積)÷3
この底面積は ある底図形の量(この場合は円、四角形、三角形、 多角形、・・・)
3は 3次元 の3 です。
この理由はxnの積分がx(n+1)/(n+1)
で、次数がnから、n+1に変化し、係数をみてください。
n+1で割っている状態になっています。

NO.229 12/13 Junko 円錐の体積(3)
円錐に限らず、底面がどんな形をしていようとも、「*錐」という
立体の体積Vは、
V=(1/3)×(底面積)×(高さ)で求めることができます。
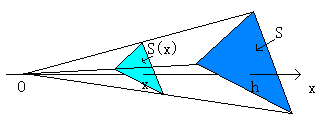
左の図のように「*錐」の頂点が原点に、
そしてx軸が底面に対して垂直になるように配置します。
底面積はS、高さはhとします。
x軸に垂直に任意の点xにおいて切ると、
そこに現れた切り口は必ず底面と相似になります。
原点からの距離の比はx:hですから、
その面積比はx2:h2になります。
x2:h2=S(x):S
S(x)h2=Sx2
S(x)=(S/h2)x2
この断面積が距離の2乗に比例するというところが、
「みそ!」なのだと思います。
これは底面の形によりません。
頂点の場所も、底面の真上である必要はありません。
(上の図でx軸は底面を通過している必要はありません。)
そして、断面積を積み重ねていくのが積分です。
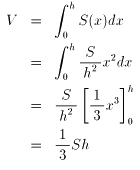
x2を積分することから、(1/3)という係数が出てくるわけですが、
これを小学生に実感してもらうのは無理がありますよね・・・。
理屈は後から勉強してもらうにしても、まず事実だけ伝える、
ということがあってもいいのではないかと思います。
(やや逃げの部分もありますが・・・。)
ただ教える側としては、もっといろいろなことを勉強すればきちんと
裏付けできるんだよという含みをもった上で、
「ちょうど1/3になるなんて本当に不思議だよねえ!」
という思いを伝えたいなあと思います。
いつかきっと、「そういうことだったのかあ!!」という感動を
得てくれるでしょう。

 E-mail
E-mail
 戻る
戻る
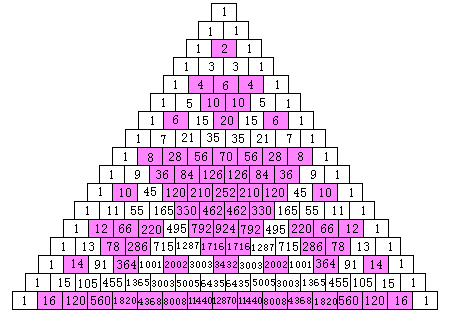

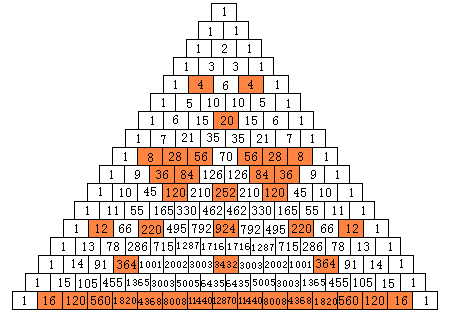


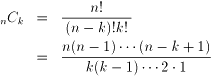





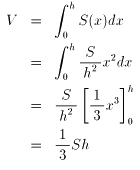
 E-mail
E-mail
 戻る
戻る