MONDAI20

２０．飛行機の問題

夏休みを利用して、飛行機で旅行される方もいらっしゃるでしょうね。
飛行機にのったつもりで次の問題に挑戦してみてください。

パイロットが真南に１００キロ、それから東に１００キロ、そして北に１００キロ飛びました。すると彼は飛び立った地点に戻ってくるという。さて彼はどこから出発したのでしょう。
答えは１ヶ所ではないよ！

問題の出典

別冊サイエンス　ひらめき思考

マ－チン・ガ－ドナ－

日経サイエンス社

答えと解説

解答・その１

（ペンネ－ム：Hungry Bear）

答は、北極点（＊）ですが、まだ他に答があるのですか？もう少し考えてみます。

（＊）正確には「磁北」です。この場所は、北カナダのバサースト島の近くにあり、地図上の北極点から約１６００ｋｍ離れているそうです。ここでの磁石は、Ｎ極が真上を指しますので、もしも磁石だけで飛行機を飛ばそうとすれば、南は真上になり、宇宙へ飛び出すことになります。

ところでこれって「数学」の問題なんですか？

解答・その２

（ペンネ－ム：うじちゃん）

答えは「北極点です」
ちなみに東へ進む北極点での角の大きさは1ラジアンですな．

解答・その３

（ペンネ－ム：水の流れ）

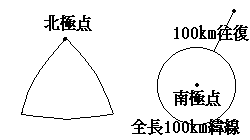
答え、１つはよく知っている　北極点
もう１つは　次の無数の地点
南半球で、緯線の長さが全長100ｋｍあり、この緯線上のどの地点でもよく、ここから、北方へ100ｋｍの距離を保つ緯線上のすべての地点

解答・その４

（ペンネ－ム：Idaho Potato）

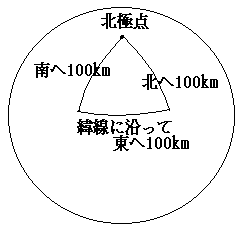
真っ先に思い付くのは、「北極点」という解です。
北極付近に限ると、解はこの１ヶ所のみですが、南極付近を考えてみると、ほかにも解があることが分かります。

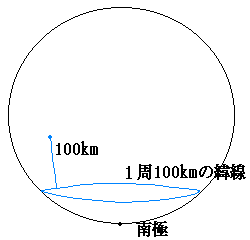
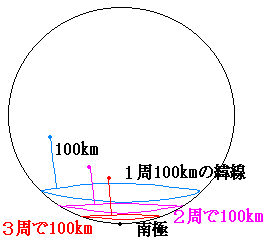
要するに、「東に100キロ」のステップが、ちょうど緯線1周になっていればよいのです。 1周といわず、2周でも3周でも、とにかく元の場所に戻ってくればよいわけです。

というわけで、南極付近の解は、nを任意の正の整数として、「緯線の周の長さが(100/n)キロであるような緯度から 100キロ北にあたる地点」（経度は何でもよい）と表せます。
周が(100/n)キロの円の半径は、 (100/n)/(3.14*2) ≒ (16/n) キロですから、南極付近の地表面を近似的に平面と考えて、解は、南極点からおよそ116キロ、108キロ、105.3キロ、104キロ… 離れた地点、ということになります。

まとめ

「Idaho Potato」さんの解答が完璧ですね。まとめてみます。

北極点
緯線に沿って地球を１周するとほぼ円を描きます。
その円の中で、南半球にあり、１周が100kmのものが存在するはずです。
赤道は１周ほぼ40000km （1メートルの起源は、北極からパリをとおって赤道までの子午線の距離の1000万分の1と定義したことによるのだそうです。）ですから。
その円周上の任意の点から真北に100km進んだ地点が答えです。
従って、無限に存在します。
先程は１周100kmの円を考えましたが、２周で100km、３周で100km、４周で100km・・・でもいいはずです。
こう考えても無限に存在することになります。