俀丏柺愊偺栤戣
廲侾cm丄墶侾侽cm偺挿曽宍偺僥亅僾俙俛俠俢偵丄侾cm偛偲偵俙俛偵暯峴偵慄傪堷偄偰偄傑偡丅 懳妏慄俛俢傪堷偄偰丄恾偺傛偆偵幬慄傪擖傟傞偲偒丄幬慄偺晹暘偺柺愊偺榓偼丄偄偔傜偵側傞偱偟傚偆偐丅

摎偊偲夝愢
俀丏柺愊偺栤戣
廲侾cm丄墶侾侽cm偺挿曽宍偺僥亅僾俙俛俠俢偵丄侾cm偛偲偵俙俛偵暯峴偵慄傪堷偄偰偄傑偡丅
懳妏慄俛俢傪堷偄偰丄恾偺傛偆偵幬慄傪擖傟傞偲偒丄幬慄偺晹暘偺柺愊偺榓偼丄偄偔傜偵側傞偱偟傚偆偐丅

夞摎偦偺侾乮戜宍朄乯
戜宍偺柺愊偑丄乮忋掙亄壓掙乯亊崅偝亐俀丂偲偄偆偺傪巊偆丅
俛俢傛傝忋偺晹暘傪侾俉侽並夞揮偝偣傞偲壓偺晹暘偲廳側傞偐傜慜幰偺柺愊傪媮傔丄
俀攞偡傟偽傛偄丅
俛俢傛傝忋偺晹暘偵偮偄偰偼丄
乷(1+0.9)+(0.8+0.7)+(0.6+0.5)+(0.4+0.3)+(0.2+0.1)乸亊1亐2=5.5/2
廬偭偰丄偙傟傪俀攞偟偰丄5.5cm2偱偁傞丅
夞摎偦偺俀乮偢傜偟朄乯
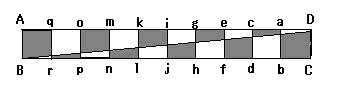
忋偺恾偺傛偆偵奺捀揰偵柤慜傪偮偗傑偡丅
偙傟傪俛俢偵偦偭偰偢傜偟傑偡丅

偡傞偲偙偺傛偆偵側傝傑偡丅
崅偝偼1.1cm偵側傞偺偱丄柺愊偼1.1亊1亊5=5.5cm2偲偄偆傢偗偱偡丅
夞摎偦偺俁乮慻傒崌傢偣朄丒偦偺侾乯
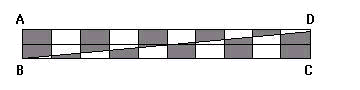
忋偺恾偺傛偆偵俙俛偺拞揰偲俠俢偺拞揰傪寢傇捈慄傪傂偔丅
偡傞偲丄幬慄偑擖偭偰偄傞挿曽宍偑俇偮偱偒傞丅
俇偮偺挿曽宍偺柺愊偼丄0.5亊6=3cm2
嵍壓侾乛係偺晹暘傪
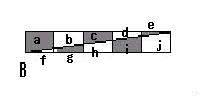
偲偍偔偲丄倎亖倞丄倐亖倝丄們亖倛丄倓亖倗丄倕亖倖側偺偱丄傑偲傔傞偲

偲偄偆偙偲偵側傞丅
柺愊偼丄0.5亊5亐2=2.5/2
塃忋侾乛係偺晹暘傕摨偠傛偆偵偡傞偲丄柺愊偼2.5/2
偙偺俀偮傪偨偡偲2.5cm2
廬偭偰丄3+2.5=5.5cm2

忋偺條偵曗彆慄傪偄傟傑偡丅
偙偺晹暘偺柺愊偼丄廲0.1亊墶1=0.1
0.1亊5=0.5

偙偺晹暘偼丄廲1亊墶1=1
1亊5=5
崌傢偣偰丄0.5+5=5.5偲側傝傑偡丅
夞摎偦偺俆乮敀崟斾棪朄乯
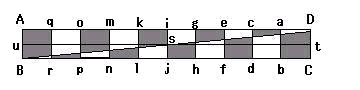
1cm偛偲偵嬫愗偭偨強傪忋偺恾偺傛偆偵偍偔丅
俙俛偺拞揰倳偲俠俢偺拞揰倲傪寢傃丄倝倞偲偺岎揰傪倱偲偡傞丅
倱偼俛俢忋偺揰偱傕偁傞丅
傛偭偰丄巐妏宍俙倝倱倳偲巐妏宍倳倱倞俛偼崌摨側偺偑傢偐傞丅
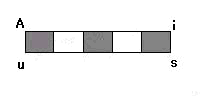
師偵巐妏宍俙倝倱倳偩偗傪尒傞偲
幬慄晹暘偲敀偄晹暘偺柺愊偼俁丗俀偵側偭偰偄傞丅
巐妏宍倱倲俠倞傕摨條丅
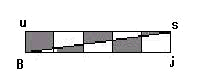
偦偟偰丄巐妏宍倳倱倞俛傪尒傞偲
傑傫拞偺巐妏宍偼懳妏慄傪偼偝傫偱崌摨丅柺愊偼侾丗侾丅丒丒丒嘆
挿曽宍偺懳妏慄側偺偱佢倳倱俛亖佢倞俛倱偱椉抂偺巐妏宍傕崌摨偱
幬慄晹暘偲敀偄晹暘偺柺愊偼侾丗侾丅丒丒丒嘇
巆傝俀偮偺巐妏宍傕摨條丅柺愊偼侾丗侾丅丒丒丒嘊
嘆嘇嘊傛傝丄巐妏宍倳倱倞俛偺幬慄晹暘偲敀偄晹暘偺柺愊偼摨偠偵側傞丅
巐妏宍倝俢倲倱傕摨條丅
侾曈偑1cm偺巐妏宍偑侾侽偙偮側偑偭偰偄傞偺偱柺愊偼10cm2
幬慄晹暘偺柺愊丗敀偄晹暘偺柺愊亖侾侾丗俋
側偺偱丄幬慄晹暘偺柺愊偼5.5cm2
夞摎偦偺俆丒僐儊儞僩
柺愊傪捈愙媮傔偢丄慡懱偺柺愊偲偺斾偱媮傔傞偲偄偆揰偱偡丅
旕岠棪偩偲偄偆恖傕偄傞偐傕偟傟傑偣傫偑丄巹偼偲偰傕儐僯亅僋側傾僀僨傾偩偲巚偄傑偡丅
夞摎偦偺俇乮奼戝朄乯
偙偺恾宍傪丄廲偵侾侽攞偡傞丅
偡傞偲幬慄晹暘偺柺愊傕侾侽攞偵側傞丅
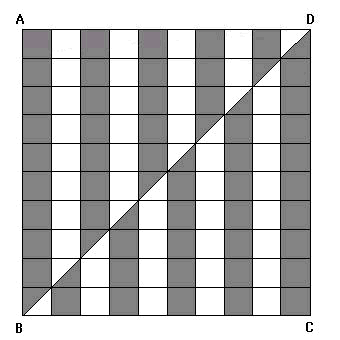
偙偺恾宍偵偍偄偰丄幬慄晹暘偼柺愊侾cm2偺惓曽宍偑俆侽屄丄
柺愊侾乛俀cm2偺捈妏擇摍曈嶰妏宍偑侾侽屄丄
偩偐傜偁傢偣偰柺愊偼俆俆cm2
廬偭偰丄傕偲偺幬慄晹暘偺柺愊偼丄5.5cm2偱偁傞丅
乮偙偺夝朄偼壓婰偺弌揟尦偺杮偵婰嵹偝傟偰偄傞傕偺偱偡丅乯
傑偲傔
奺夞摎偵柤慜傪偮偗偨偺偼巹偱偡丅偛椆彸壓偝偄丅
悢妛偺栤戣偵懳偟偰偼丄堦墳摎偊偼堦捠傝偵掕傑傞偗傟偳傕丄
偦偺摎偊偵帄傞摴偺傝偼偝傑偞傑偱偡偹丅
摎偊傊偺摴偺傝偑侾偮偱側偄偲偙傠偑悢妛偺偍傕偟傠偄偲偙傠偱偁傝丄
傑偨偳偺摴傪捠偭偰傕昁偢摨偠捀忋偵偨偳傝拝偗傞偲偄偆偺偑
悢妛偺偡偛偄偲偙傠偩偲巚偄傑偡丅
崱夞丄夝朄傪俇偮偽偐傝徯夘偟傑偟偨偑丄
偦傟傜傪撉傫偱偄偔偲丄摎偊偼5.5cm2埲奜偵偼偁傝偊側偄丄
偲偄偆婥帩偪偵側偭偰偒傑偡偐傜晄巚媍偱偡丅
儊亅儖偱偺夞摎丄偳偆傕偁傝偑偲偆偛偞偄傑偟偨丅
栤戣偺弌揟
僺亅僞亅丒僼儔儞僋儖偺僷僘儖傛傝柺敀偄拞妛擖帋偺嶼悢
島択幮

 栠傞
栠傞