問題168 年賀状の問題
人口1000人の村に1000軒の家があり、村の人はみんな1人で住んでいます。
この村では、お正月にすべての村の人が、自分の家から一番近い距離にある家に1枚だけ
年賀状をだします。家どうしの距離はみんな違います。
また、村の外から年賀状はきません。
さて、この村では、1人の村の人が最高で何枚の年賀状をもらえますか。
その理由も考えてください。
問題の出典
パズル気分で算数オリンピック
東大算数研究会
講談社
第5回算数オリンピック 決勝問題
解答
解答・その1
(ペンネ−ム:オヤジ)
∴最高で、5枚年賀状が、もらえる。
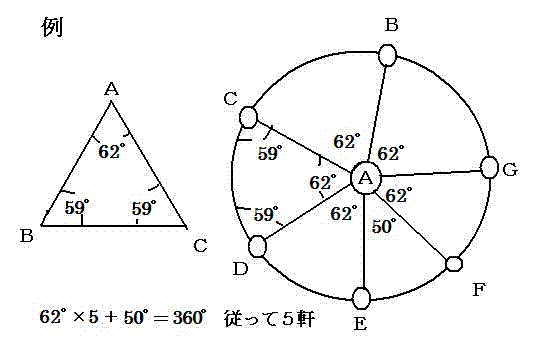
∵ 1000軒のなかで、他と少し離れて7軒が,正六角形の頂点と中心に、配置されたとすると,
中心の家は、年賀状が6枚もらえるが、
これは、各家どうしの距離が違う仮定から年賀状が6枚以上もらうことはあり得ない。
ここで,中心の家以外の,一軒をのぞき半径を変えずに正五角形に近いような
但し各二軒の距離を少し変え,全て異なる距離に配置し中心の一軒を5軒からの
距離が最短である条件を満たしながらも中心から5軒間の距離も全て異なる
ように中心の家も僅かに移動すると,五角形の中心に近い家が,
5枚年賀状がもらえる。
解答・その2
(ペンネ−ム:迷子の雄猫)
題意では、家同士の距離はみんな違う。
B家〜G家から、A家に6枚の年賀状が届いたとする。
そうすると、A家を中心としてB家〜G家の6軒を、
A家から見てこの順序で時計回りになるように配置したとすると、
三角形ABC,ACD,ADE、AEF,AFG,AGB全て不等辺三角形になる。
角BAC、角CAD,角DAE、角EAF,角FAG,角GAB全てを加えると
360度である。
不等辺三角形ABCの辺の長さを考える。
辺ABと辺BCでは辺ABのほうが短く、
辺ACと辺BCでは辺ACのほうが短いのだから、
3辺のなかでは辺BCが一番長くなる。
さて、辺BC上に点P,Qを、
AB=BQ、AC=CPとなるように取ったとする。
二等辺三角形の底角は等しいから、
角CAP=角CPA
角BAQ=角BQA
角BAC=角BAQ+角QAC=角CAP+角PABなので、
三角形の内角の和は180度で一定であるから、
角BACは角ABCよりも、また角BCAよりも大きくなる。
よって、180度の三分の一(60度)よりも、角BACが大きくなるから、
同様に角CAD,角DAE、角EAF,角FAG,角GAB全て60度よりも大きくなる。
よって、角BAC、角CAD,角DAE、角EAF,角FAG,角GAB全てを加えると
360度よりも大きくなる。よって矛盾する。
よって、ある家に6枚の年賀状が届くことはありえない。
A家を中心としてB家〜F家の5軒を、
A家から見てこの順序で時計回りになるように配置したとすると、
AB,AC,AD,AE,AFの長さを順に1001,1002,1003,1004,1005
それぞれの角度を72度とすると、
BC,CD,DE,EF,FBの距離が順に
1,177.3 1,178.5 1,179.7 1,180.9 1,179.1
となり題意を満たす。
よって、最高5軒。
解答・その3
(ペンネ−ム:haya)
貰える年賀状の最大数は 5 枚です。
【解き方】
沢山の年賀状を貰える家は車輪のハブのような場所に位置する家です。
村人の家を幾何平面上の点に置き換えて考えたときに、正五角形までは辺の長さが中心からの半径より大きい。
勿論、この場合は家同士の距離が全て違うことに反しますが、充分に図形を大きくし、
各点の位置を互いに微小寸法ずらすことによって題意の関係にできますから、
中心の近傍に位置する家は最大5枚の年賀状が貰える。
これに対して、正六角形以上の図形では中心からの距離が辺の長さ以上になってしまうので
6枚以上貰うことはできないということです。
解答・その4
(ペンネ−ム:teki)
答え 5枚
平面で考えてよければ、正六角形を考えれば、6つの頂点と中心の点の距離がすべて等しくなります。
つまり、これ以上点を増やすと、中心の点と周りの点の距離より短い点同士が必ず発生します。
1点の周りに5点をうまく配置すると、中心の点からの距離より短い点同士が現れないので、これが最大ですよね。
これって、空間で考えるとどうなるんでしょう?
私には難しすぎます><
解答・その5
(ペンネ−ム:のっこん)
△OABにおいて OA=1, OB=1-a, AB=1+a (0<a<1)とする
この時、AはBよりもOの方が近いので年賀状はOに出す
BはAよりもOの方が近いので年賀状はOに出す
∠AOB=θとすると 余弦定理より
cosθ=(1-4a)/(2-2a)=1/2-3a/(2-2a)<1/2
cosθ<1/2 だから θ>60°
よってOの周りに6点A,B,C,D,E,Fをとり
ABよりもOA,OBを小さく、
BCよりもOB,OCを小さく、
CDよりもOC,ODを小さく、
DEよりもOD,OEを小さく、
EFよりもOE,OFを小さく、
FAよりもOF,OAを小さく、とすることはできない
Oの周りが360°よりも大きくなってしまうからである
Oの周りに5点A,B,C,D,Eをとり
ABよりもOA,OBを小さく、
BCよりもOB,OCを小さく、
CDよりもOC,ODを小さく、
DEよりもOD,OEを小さく、
EAよりもOE,OAを小さく、することは十分に可能なので
1人がもらえるのは最も多くて5枚である
解答・その6
 (ペンネ−ム:杖のおじさん)
(ペンネ−ム:杖のおじさん)
答え 5通です。
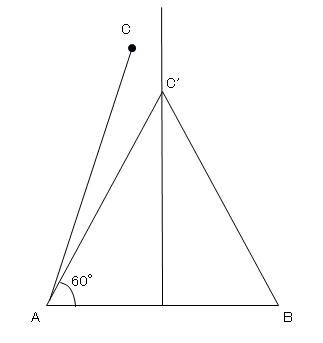
下の図のようにAの家が隣の家から2通年賀状を貰う事が出来る条件は∠BACが∠ABCより大きく、
かつ∠BACが∠ACBも大きくなければならない。すなわち他の角より大きくなければなりません。
三角形の内角の和は180度なので180度÷3=60度です。従って60度以上なければだめです。
Aの家を中心として周囲の家から手紙を貰うには360度の中に60度以上の角度を持った
三角形が幾つ入るか考えると5軒と分かります。
解答・その7
(ペンネ−ム:スモークマン)
・最初の2点 P1, P0 を決める...
・次の3点目はP1P0の垂直二等分線のP0 側で...
P1から半径が P1P0 の円の外側に点P2が取れる...
このとき...P2P1>P2P0を満たす。
このとき...角P2P0P1>60°
・同様に考えて行くと...360/60=6 なので...P5までしか取れない...
・最後の点P5は...角P1P0P5=360-60*4+α>60のように取ることが可能
けっきょく...P0の人が最大で(も)5枚の賀状がもらえる。
解答・その8
(ペンネ−ム:ykak)
答え 5枚
 考え方
考え方
年賀状をもらう人をAとし、Aに年賀状をくれる人で一番近いところに住んでいる人をBとする。
次に、AがB以外の人から年賀状をもらえる条件について考える。Aに年賀状をくれる人で2番目にAに近い人をCとすると、AC間の距離(以後これをACと書く)は、ABよりより大きく、かつACはBCより小さくなければならない
(そうでなければCはBに年賀状を送ることになるから)。――― (1)
今A、B(それぞれが住んでいる地点もA、Bなどと記載することにして)と、C’という点を取り、A、B、C’をそれぞれ直線で結んでできる三角形が正三角形であるとすると、AB、BC’、AC’は全て等しくなる。
(1)の条件は、AC>ABかつAC<BCということであるが、正三角形ABC’を基準にして、この条件に合うような点Cの位置をを決めることにすると、正三角形ABC’の点C’から直線ABに垂線を下ろしたとして、Cはこの垂線よりA側にあって、AC>AC’
となる位置になければならない(Cは2番目にAに近い家だから)ということになるが、この場合、
∠C’ABは60度だから、∠CABは60度より大きくなる。――― (2)
同様にして、Aに3番目に近い人をDとし、DがAに年賀状を送ってくれるためには、
∠DACが60度より大きくなければならない、というようにして、Aの周りに年賀状を
送ってくれる人を配置していくと、5番目までは上の条件に合う人を配置できる。
ところが6番目に配置する人をGとすると、∠GAB(C、D、E、Fを含む大きいほう
の角度)は300度を越えるから、∠GABの小さいほうの角度は60度より小さくなってしまうが、
そうなると(2)で言ったことから、GA>ABとはできないことになるから、
6番目の人を(1)の条件に合うように配置することはできないということが言える。
また、Aの周りに配置したBからFの外側に配置した人は、Aとの距離より、
BからFのうちの誰かとの距離のほうが近くなるから、この配置は意味を持たない。
従って、最大配置できる人は5人ということになり、貰える年賀状は5枚になる。
解答・その9
(ペンネ−ム:MVH)
まず、3人(Aさん、Bさん、Cさん)だけの場合を考えます。
AさんがBさん、Cさんから年賀状を受け取るとします。このとき、題意より、
AB<BC かつ AC<BC
が成立します。つまり、三角形ABCにおいて、辺 BC が最も長い辺であることが導かれました。
これは、∠A が最大の角であることを意味します(これは明らかとします)。
ここで、∠A ≦ 60°とすると、三角形の内角の和が 180°未満となって不適なので、
∠A > 60°を得ます。
さて、ここで、Aさんが年賀状を最高で何枚もらえるかを考えます。
Aさんを原点とする座標平面を用意するとき、Aさんに年賀状を出す人一人を軸上に置き、
次々に反時計回りに配置していきます。
このとき、上で得られた事実によると、一周はですので、6人は配置できません。
よって、高々5人までしか配置することはできないことが分かりました。
一方、5人を配置することが可能です(具体例を構成することは容易なので省略します)。
従って、本問の答えは、5枚となります。
〔解き終えて〕
一見しただけでは、何から手を付けて良いか迷いましたが、小さい数から調べると意味が分かりました。実験は大切ですね。
解答・その10
(ペンネ−ム:SOU)
問題で言っている家は、全て点Pn=(Xn,Yn,Zn)
として存在させる。
全てのPiに対して、Piと最も距離の近いPjを探し、
選ばれた番号のZj要素の値を1増やすことにする。
また、題意から任意のi,j に対して2点Pi,Pj
間の距離は異なるものとする。
点P0をxy直行座標系の原点に置く。
Z0の値を出来るだけ可能な限り多くするようにする。
P1をX軸上正の方向に任意に設置する。
P0とP1との距離をd1とする。
次に、点P2 をどこに置くかを考える。
置ける場所はP1 への距離よりもP0への距離の方が短くなるような場所でなければならない。
即ち、P0とP1との垂直二等分線により分けられるXY平面の中で、
P0 を含む領域(全ての距離が異なるということから、境界線は含まない)におかねばならない。
また、P1 からP2 への距離がP0への
距離を下回ってはならないため、P2 は、P1 を中心とした
半径d1 の円の外部の領域に置かねばならない。
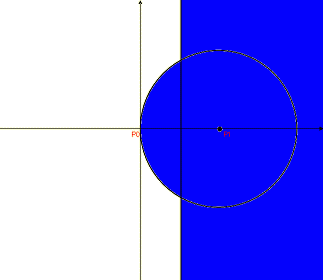
この時点でZ0 = 1
即ち垂直二等分線と円により分けられる四つの領域のうち
P0を含む部分がP2を置ける候補領域になる。
y>0 の部分と y<0 の部分、どちらで考えても同じなのでy>0 にP2を置くことを考える。
またP0とP2によっても同様に垂直二等分線及び円が作られ
P3を置ける領域が狭まる事を考えると、
P0とP2を通る直線とx軸との成す角は可能な限り小さく取らねばならない。
その角が限りなく小さくなるためにはP0とP2を通る直線がx軸となす角が小さくなることである。
そのようなP2の位置は円と垂直二等分線との交点が最もその角を小さく取れるが、
境界線上には置けないので、交点の近傍でかつ対象の領域にある点をP2としてとる。
(P2 = (d1/2 - ε,√3d1 + ε) のようになる。)

この時点でZ0 = 2
即ち
∠P2P0P1 > 60°
となる。
同様にして、P0とP2 の垂直二等分線を考え、P2を中心とする円を作り、
P3を置く場所を考えると、やはり円と直線の交点の近傍となる。
∠P3P0P1 > 120°

この時点でZ0 = 3
以下、同様にして
∠P4P0P1 > 180°
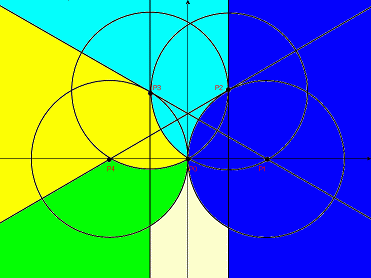
∠P5P0P1 > 240°

となる。
この時点でZ0 = 5
ここでP6 について考えると、
∠P6P0P1 > 360°
なのでP6 の位置はどうしてもPP1 の領域に入ってしまう。
即ちP6 を置く場所が存在しない。
以上のことから、5 が限界なので、
最大で 5 //
解答・その11
(ペンネ−ム:転位反応)
村は同一平面上にあって、家は点で表現できるものとする。
先ず、「家どうしの距離はみんな異なる」という制約を外して考えると、
できるだけ多くの年賀状を受け取るためには次の条件が必要である。
(1) 一軒の家を中心とする円周上に複数の家が存在する
(2) 円の半径 < 円周上の隣接する家どうしの距離
半径rの円に内接する正多角形を考えて、
円の中心と正多角形の頂点に家が存在するものとする。
正六角形の場合には一辺の長さはrに等しくなるので、正五角形の場合が
上記 (1) (2) を満たす最大の整数である。
下図は、円の中心に家O、正五角形の頂点に家A〜Eを配置している。
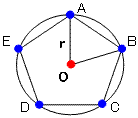
さて、「家どうしの距離はみんな異なる」という制約を加えて考える。
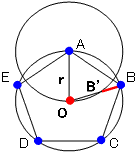
点Aを中心とする半径rの円と線分OBの交点をB’とすると、
線分BB’(両端を含まない)上の任意の点は、隣接する点Aからの距離が
rより大きく、かつ、点Oからの距離はrより小さい。
同様な議論が他の頂点についても成り立つので、それぞれの相当する
線分(両端を含まない)上の点を上手く選ぶことによって、全ての点どうしの距離を変える事ができる。
よって、題意を満たす年賀状の枚数は5枚である。
解答・その12
(ペンネ−ム:夜ふかしのつらいおじさん)
○はじめに考えたこと
「この村が何次元の世界なのか」で答えが違うのではないかと思いました。
・1次元の世界で考えます。
Oを一番多くの年賀状をもらう人の家とし、他の人の家をA,B,C,・・・とします。
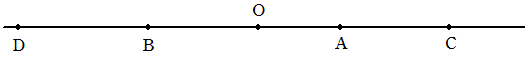
Oから右の方は、OA<ACであれば、Aから一番近い家はOなのでAから1通きます。
Oから左の方は、OB<BDであれば、Bから一番近い家はOなのでBから1通きます。
Oには合計2通きます。
この状態を変えずに他にOに年賀状を出す家をおくことができません。
この村が1次元の世界でできているなら、2通もらえます。
・999次元の世界を考えます。(図は3次元、説明の表は4次元ですが・・・)
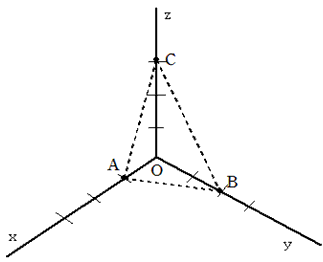
999次元の世界でも
2点 A(a1,a2,a3,・・・,a999)と
B(b1,b2,b3,・・・,b999) との距離 d は、
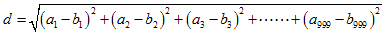
です。Oを原点とします。
点Aをx軸上、Bをy軸上、Cをz軸上、・・・に、OA<OB<OC<・・・となるようにとります。
結果が見やすいので次のように点をとり、2点間の距離の表をつくります。
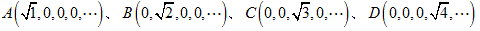
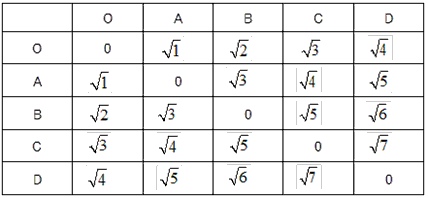
どの点からでもOまでの距離が一番近いです。(自分自身を除いて)
だからOは、999通の年賀状をもらえます。
○次に2次元で考えたこと
点Oを一番多く年賀状をもらう家とします。
まずAを配置し、次にB、C、D、・・・と順に家を配置していきます。
Bは次の条件を満たします。
(1)Aの最寄りがOのままであるためには、Bは円Oの外部になくてはなりません。
(2)Bの最寄りがOであるためにBはOAの垂直二等分線aのO側になくてはなりません。
(図のうすい青と青のところ)
同様にCは、さらに円Bの外部で、OBの垂直二等分線bのO側になくてはなりません。
(図の青のところ)
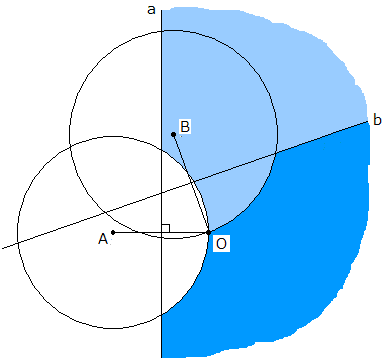
図がみにくくなるので、改良して、正三角形OAA’をつくり、AA’の延長上にBをとります。
すると、∠B=60−α°、∠A=60°、∠AOB=60+α°となります。
だからAからみるとAO<AB、BからみるとBA<BOです。
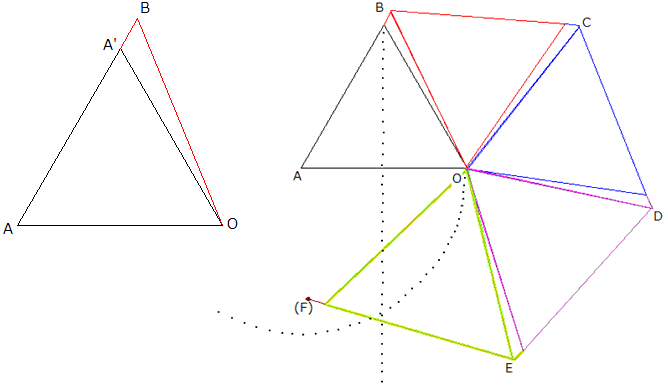
次にOBを1辺とする正三角形を考えて同様にBB’の延長上に点Cをとります。
これを繰り返すと、右の図のようになります。
こうすると、A,B,C,D,Eの5点まではうまくいきますが、FでOよりAの方が近くなってしまいます。
(円Aの外部で垂直二等分線AOのO側に点Fをとることができません)
こう考えると5軒から年賀状がきます。
仮に、家どうしの家の距離が等しくてもよいとして平面の中で考えると左の図のようになります。
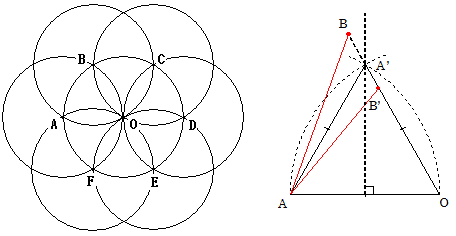
Bの位置を動かすことを考えます。(家どうしの距離を変えるため)
右の図で△OAA'は正三角形です。
このときBはA’の位置を直線OA’上で動かすことができません。
OA’<OBとすれば、垂直二等分線のA側になるのでBの最寄りは、OではなくAになります。
OA’>OB’とすれば、円Aの内部に入るので、Aの最寄りは、OではなくB’になります。
○さらに3次元で考えたこと
はじめは家どうしの家の距離が等しくてもよいとして球の表面に家を配置することを考えます。
一番効率が良い家の置き方として、正20面体の頂点に家を置くことが考えられます。
隣り合うどの家も等距離にあります。
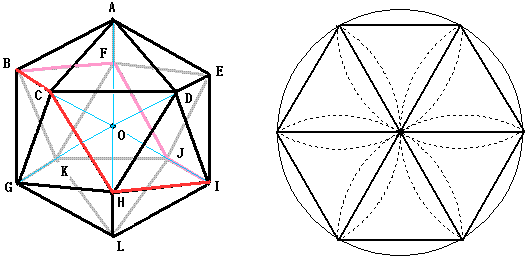
隣どうしの家をなるべく大円からそれないように結んでいくと、左図の赤い線のようになります。
この赤い線上には、6軒の家があります。
この線は折れ曲っているので中心のOとの距離より他の隣の家との距離の方が長くなります。
大円上に6軒の家があれば、隣り合うどの2軒の家の距離も等しくなります。
下の図の△OAA’は、OA=OA’<AA’の2等辺三角形です。
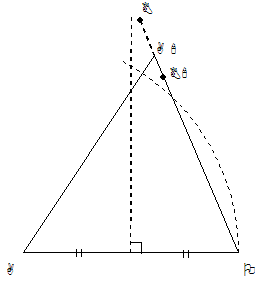
今度は、平面内の場合とは異なり、直線OA’の延長上を動かすことができます。
円Aの外部で、垂直二等分線のO側であればよいことになります。
正20面体には頂点が12個あります。
この関係を崩さないように家を配置すれば空間内では、12軒から年賀状がくることになります。
正解者
| teki | スモークマン | のっこん |
| オヤジ | haya | 迷子の雄猫 |
| 転位反応 | 杖のおじさん | SOU |
| ykak | 夜ふかしのつらいおじさん | MVH |
コメント
新年あけましてめでとうございます。
最近は、メールや電話などで新年のあいさつをする人も多く、年賀状が減っているようですね。
皆さまのところには、何通くらい届いたでしょうか。
さて、今回の問題ですが、何次元で考えるのでしょうか、という質問をお寄せいただきました。
平面(2次元)でとお願いしました。3次元で考えるといったいどうなるのだろうかと
思っていましたら、夜ふかしのつらいおじさん
が考えてくださいました。
165.製品検査の問題に引き続き、
たけしのコマ大数学科の
制作担当者から、この問題について問い合わせがありました。
今度こそしっかり見なくちゃ!(放送日未定)
 top
top