���165�@���i�����̖��
����H��ŁA�P���ĂP�O�O�O�~�̗��v�鐻�i���P�P����܂����B
�������A���̒��̂P�����邱�Ƃ̂ł��Ȃ��s�Ǖi�ł��邱�Ƃ��킩��܂����B
�����ŁA���̐��������@�B���g���āA�Ǖi��I��Ŕ��邱�Ƃɂ��܂����B
�i�@�B�̐����j
(1) �P��ɁA�����̐��i�ł����ׂ邱�Ƃ��ł��܂��B
(2) �P�ׂ邽�߂ɁA�P�O�O�O�~�̔�p��������܂��B
(3) ���ׂ����i�̒��ɕs�Ǖi��������Ȃ������ꍇ�A���ׂ����i�͂��ׂĔ��邱�Ƃ��ł��A�e�P�O�O�O�~�̗��v�������܂��B
(4) ���ׂ����i�̒��ɕs�Ǖi�����������ꍇ�A�ꏏ�ɒ��ׂ����i�����ׂĕs�Ǖi�ƂȂ��Ă��܂����邱�Ƃ��ł��Ȃ��Ȃ�܂��B
���Ƃ��A���̋@�B���g���ĂP�����i�ׂĂ����ƁA���̂悤�ȉ\�����l�����܂��B
���P�����ׂĂ����āA�ł��^�̂����Ƃ���
�P�߂ɕs�Ǖi��������B
�����ׂ�̂ɂP�O�O�O�~������A�c��P�O��A�e�P�O�O�O�~�̗��v��B
�@�P�O�O�O�~�P�O�|�P�O�O�O���X�O�O�O�~�̗��v
���P�����ׂĂ����āA�ł��^�̈����Ƃ���
�P�O�߂܂ŕs�Ǖi��������Ȃ��B
���Ō�̂P�́A���ׂȂ��Ă��s�Ǖi���Ƃ킩��B
�@����܂ł̐��i����A�e�P�O�O�O�~�̗��v�邪�A���ׂ�̂ɂP��ɂP�O�O�O�~�������Ă���̂ŁA���v�͂Ȃ��B
���ׂ���⏇���ɂ���Ă������̒��ו����l�����܂����A���̒��Ł��ł��^�̈����Ƃ�����
�����闘�v����ԍ�������ɂ͂ǂ̂悤�Ȓ��ו�������悢�ł��傤���B
���̒��ו��ƁA���̏ꍇ���ł��^�̈����Ƃ����ɓ����闘�v���Ă��������B
���̏o�T
�p�Y���C���ŎZ���I�����s�b�N
����Z��������
�u�k��
��P��Z���I�����s�b�N�@�������
�����Ɖ��
�E����1
�i�y���l�|���F�̂�����j
�ŏ���n�A����(n-1)�A���̎���(n-2)�A�E�E�E�E�E�ƌ������Ă������Ƃɂ���A
�ǂ�ɕs�Ǖi���܂܂�Ă��Ă������� 1000(n+1)�~�ƈ�肾����A��� 1000(10-n)�~�����v�ƂȂ�B
n=5 �̎�
�@5��4��2�Ƃ��Ă��A5��3��3�Ƃ��Ă�
�@�ł��^���������̗��v�� 1000�E5=5000(�~�j
n=4 �̎�
�@4��3��2��2�Ƃ����
�@��ɗ��v��1000�E6=6000(�~�j
n=3 �̎�
�@3��2��2�Ƃ��Ă�
�@3�{2�{2��7��11 �ƂȂ�s��
����� 4��3��2��2�ƌ������Ă�����
�@�ł��������v�i6000�~�j��������
�E����2
�i�y���l�|���F�X���[�N�}���j
�Ŋ�����Q�Ԗڂɔ���=�s�Ǖi���Ŋ�����2�Ԗڂɓ����Ă� or �Ŋ��ɓ����Ă邱�Ƃ�
�����Ȃ̂�...�������ōŏ���1�ɂ��Ă����Α����͍ŏ�...
���l��...���̑O�̐����s�Ǖi�ł����̌��̐��Ɠ�������Α����ŏ�
�܂�...2-(1-1)
���̑O��...
4-(2-1-1)
���̑O��...
8-4-2-1-1
����...�S����11�Ȃ̂�...
4-3-2-1-1
4:7-1=6,3:8-2=6,2:9-3=6,1:10-4=6
�������傭...�ň��ł�6000�~�ׂ̖���
�E����3
�i�y���l�|���F�I���W�j
�@�B�Œ��ׂ�ő����ɂ���ďꍇ��������B
�@�E�ō��P�O�܂Œ��ׂ�Ηǂ��B�]���ĂP�O�S�ėǕi�̏ꍇ�͍l���Ȃ��Ƃ���B
�@�E�s�Ǖi�������������̒��ׂ������A�����Ƃ���B
�@�E�����珇�Ԃɒ��ׂ����Ƃ���B
�i�T�j�ő����P�̏ꍇ
�@�@�P�C�P�C�P�C�P�C�P�C�P�C�P�C�P�C�P�C�P�@�E�E�E���v�@�O�~
�i�U�j�ő����Q�̏ꍇ
�i�@�j�Q�C�Q�C�Q�C�Q�C�P�C�P�@�@�@�@�@�@�@�E�E�E���v�@�S�O�O�O�~
�i�A�j�Q�C�Q�C�Q�C�Q�C�Q�@�@�@�@�@�@�@�@�@�E�E�E���v�@�S�O�O�O�~
�@etc
�i�V�j�ő����R�̏ꍇ
�i�@�j�R�C�R�C�Q�C�Q�@�@�@�@�@�@�@�@�@�@�@�E�E�E���v�@�T�O�O�O�~
�i�A�j�R�C�R�C�R�C�P�@�@�@�@�@�@�@�@�@�@ �@�E�E�E���v�@�T�O�O�O�~
�@etc
�i�W�j�ő����S�̏ꍇ
�i�@�j�S�C�S�C�P�C�P�@�@�@�@�@�@�@�@�@�@�@�E�E�E���v�@�T�O�O�O�~
�i�A�j�S�C�S�C�Q�@�@�@�@�@�@�@�@�@�@�@ �@�@�E�E�E���v�@�T�O�O�O�~
�i�B�j�S�C�R�C�R�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E���v�@�T�O�O�O�~
�i�C�j�S�C�R�C�Q�C�P�@�@�@�@�@�@�@�@�@�@�@�E�E�E���v�@�U�O�O�O�~
�@�@�@�S�C�R�C�Q�C�P�@�@�@�@�@�@�@�@ �@�@�@�E�E�E���v�@�U�O�O�O�~
�@�@�@�S�C�R�C�Q�C�P�@�@�@�@�@�@�@�@�@�@ �@�E�E�E���v�@�U�O�O�O�~
�@�@�@�S�C�R�C�Q�C�P�@�@�@�@�@�@�@�@ �@�@�@�E�E�E���v�@�U�O�O�O�~
�i�D�j�S�C�Q�C�Q�C�P�C�P�@�@�@�@�@�@�@�@�@�E�E�E���v�@�T�O�O�O�~
�i�E�j�S�C�Q�C�Q�C�Q�@�@�@�@�@�@�@�@�@�@�@�E�E�E���v�@�T�O�O�O�~
�@etc
�i�X�j�ő����T�ȏ�̏ꍇ
�@�@�T�C���Cetc
�@�@�U�C���Cetc
�@�@�V�C���Cetc
�@�@�W�C���Cetc
�@�@�X�C�P�@�@�@�ƂȂ�A���v���T�O�O�O�~�ȏ�ɂ͐���Ȃ��̂ōl����K�v���Ȃ��B
���@�@�@�B�ɏ悹����́A�S���R���Q���P�̏�
�@�@�@�@�����闘�v�́A�U�O�O�O�~
�E����4
�i�y���l�|���F���q�̗Y�L�j
�s�Ǖi���܂����o����Ă����A���̐��i���c���Ă���Ƃ��A
�ň��̏ꍇ�ł����҂ł��闘�v���@���i���j�@�ł���킷�B
�ŏ��ɁA�P�`�P�P�̂����A�����ׂ邩���l����B
�P���ƁA�Ǖi�Ɖ����Ă����v���Ȃ��B
����ĂQ�ȏ��x�ɒ��ׂȂ��Ɩ��Ӗ��B
�܂��A�P�c���Ă��A�s�Ǖi�������ꍇ���v���Ȃ��B
����ĂQ�ȏ�c���Ȃ��Ɩ��Ӗ��B
���i�O�j���O
���i�P�j���O
���i�Q�j���O
���i�R�j���O�@�@�@�@�@�Q���ׂĕs�Ǖi�������ꍇ�A�Ǖi�͂P�B
���i�S�j���P�O�O�O�@�@�Q���ׂ�A���ʂɂ�炸�Ǖi�͂Q�B
���i�T�j���P�O�O�O�@�@�Q�`�R���ׂ�A���ʂɂ�炸�Ǖi�͂Q�B
���i�U�j���Q�O�O�O�@�@�Q���ׂ�A�Ǖi�̂Ƃ����v�͂P�O�O�O�{���i�S�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂R�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�R���ׂ�A�Ǖi�̂Ƃ����v�͂Q�O�O�O�{���i�R�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂Q�O�O�O
���i�V�j���R�O�O�O�@�@�Q���ׂ�A�Ǖi�̂Ƃ����v�͂P�O�O�O�{���i�T�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂S�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�R���ׂ�A�Ǖi�̂Ƃ����v�͂Q�O�O�O�{���i�S�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂R�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�S�ȏ㒲�ׂ�A�s�Ǖi�̂Ƃ����v�͂Q�O�O�O�ȉ�
���i�W�j���R�O�O�O�@�@�Q���ׂ�A�Ǖi�̂Ƃ����v�͂P�O�O�O�{���i�U�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂T�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�R���ׂ�A�Ǖi�̂Ƃ����v�͂Q�O�O�O�{���i�T�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂S�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�S���ׂ�A�Ǖi�̂Ƃ����v�͂R�O�O�O�{���i�S�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂R�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�T�ȏ㒲�ׂ�A�s�Ǖi�̂Ƃ����v�͂Q�O�O�O�ȉ�
���i�X�j���S�O�O�O�@�@�Q���ׂ�A�Ǖi�̂Ƃ����v�͂P�O�O�O�{���i�V�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂U�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�R���ׂ�A�Ǖi�̂Ƃ����v�͂Q�O�O�O�{���i�U�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂T�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�S���ׂ�A�Ǖi�̂Ƃ����v�͂R�O�O�O�{���i�T�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂S�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�T�ȏ㒲�ׂ�A�s�Ǖi�̂Ƃ����v�͂R�O�O�O�ȉ�
���i�P�O�j���T�O�O�O�@�Q���ׂ�A�Ǖi�̂Ƃ����v�͂P�O�O�O�{���i�W�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂V�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�R���ׂ�A�Ǖi�̂Ƃ����v�͂Q�O�O�O�{���i�V�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂U�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�S���ׂ�A�Ǖi�̂Ƃ����v�͂R�O�O�O�{���i�U�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂T�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�T�ȏ㒲�ׂ�A�s�Ǖi�̂Ƃ����v�͂S�O�O�O�ȉ�
���i�P�P�j���U�O�O�O�@�Q���ׂ�A�Ǖi�̂Ƃ����v�͂P�O�O�O�{���i�X�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂W�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�R���ׂ�A�Ǖi�̂Ƃ����v�͂Q�O�O�O�{���i�W�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂V�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�S���ׂ�A�Ǖi�̂Ƃ����v�͂R�O�O�O�{���i�V�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�s�Ǖi�̂Ƃ����v�͂U�O�O�O
�@�@�@�@�@�@�@�@�@�@�@�T�ȏ㒲�ׂ�A�s�Ǖi�̂Ƃ����v�͂T�O�O�O�ȉ�
���ł��^�̈����Ƃ����ɓ����闘�v�͂U�O�O�O�~�B���ו��͉��L�̂Ƃ���B
�P�P�̐��i�̂����S���ׂ�B �@�s�Ǖi�̏ꍇ�A�Ǖi���V�o�邩�痘�v�͂U�O�O�O�~�B �@�Ǖi�̏ꍇ�A�Ǖi���S�o�邩�痘�v�͂R�O�O�O�~�B �@�@�c��V�̐��i�̂����R���ׂ�B �@�@�@�s�Ǖi�̏ꍇ�A�Ǖi���S�o�邩�痘�v�͂R�O�O�O�~�B �@�@�@�Ǖi�̏ꍇ�A�Ǖi���R�o�邩�痘�v�͂Q�O�O�O�~�B �@�@�@�@�c��S�̐��i�̂����Q���ׂ�B �@�@�@�@�@�s�Ǖi�̏ꍇ�A�Ǖi���Q�o�邩�痘�v�͂P�O�O�O�~�B �@�@�@�@�@�Ǖi�̏ꍇ�A�Ǖi���Q�o�邩�痘�v�͂P�O�O�O�~�B �@�@�@�@�@�@�c��Q�̐��i�̂����P���ׂ�B �@�@�@�@�@�@�@�s�Ǖi�̏ꍇ�A�Ǖi���P�o�邩�痘�v�͂O�~�B �@�@�@�@�@�@�@�Ǖi�̏ꍇ�A�Ǖi���P�o�邩�痘�v�͂O�~�B
�E����5
�i�y���l�|���Fykak�j
�����@�S��ڂ܂Ŏ��̖����̒ʂ茟������B
�@�@�@�@�����Ƃ��^�̈����Ƃ��̗��v��6,000�~
�@�@�@�P��ځ@�S��
�@�@�@�Q��ځ@�R��
�@�@�@�R��ځ@�Q��
�@�@�@�S��ځ@�P��
�l����
�m�P]�@���̕��@�ŗ��v��6,000�~�ɂȂ邽�߂̏������l����B
- �P��ڂ̌����ŕs�Ǖi���������Ă����v��6,000�~�ɂȂ邽�߂ɂ́A
�P��̌�����1,000�~���g���Ă����v��6,000�~�ɂȂ�Ȃ���Ȃ�Ȃ�����A
7,000�~�̔��グ���Ȃ���Ȃ�Ȃ��B
�]���āA�P��ڂɌ������鐻�i�̌��͂S�ȉ��łȂ���Ȃ�Ȃ��B
- �Q��ڂ̌����ŕs�Ǖi���������Ă����v��6,000�~�ɂȂ邽�߂ɂ́A
�Q��̌�����2,000�~���g���Ă����v��6,000�~�ɂȂ�Ȃ���Ȃ�Ȃ�����A
8,000�~�̔��グ���Ȃ���Ȃ�Ȃ��B
�]���āA�Q��ڂɌ������鐻�i�̌��͂R�ȉ��łȂ���Ȃ�Ȃ��B
- �R��ڂ̌����ŕs�Ǖi���������Ă����v��6,000�~�ɂȂ邽�߂ɂ́A
�R��̌�����3,000�~���g���Ă����v��6,000�~�ɂȂ�Ȃ���Ȃ�Ȃ�����A
9,000�~�̔��グ���Ȃ���Ȃ�Ȃ��B
�]���āA�R��ڂɌ������鐻�i�̌��͂Q�ȉ��łȂ���Ȃ�Ȃ��B
- �S��ڂ̌����ŕs�Ǖi���������Ă����v��6,000�~�ɂȂ邽�߂ɂ́A
�S��̌�����4,000�~���g���Ă����v��6,000�~�ɂȂ�Ȃ���Ȃ�Ȃ�����A
10,000�~�̔��グ���Ȃ���Ȃ�Ȃ��B
�]���āA�S��ڂɌ������鐻�i�̌��͂P�łȂ���Ȃ�Ȃ��B
- �T��ڂ̌���������A���v��6,000�~�ɂ��邱�Ƃ͂ł��Ȃ��B
�m�Q]�@�@���ɁA���l�ɂ��ė��v��7,000�~�ɂȂ邽�߂̏������l����B
- �P��ڂ̌����ŕs�Ǖi���������Ă����v��7,000�~�ɂȂ邽�߂ɂ́A
�P��̌�����1,000�~���g���Ă����v��7,000�~�ɂȂ�Ȃ���Ȃ�Ȃ�����A
8,000�~�̔��グ���Ȃ���Ȃ�Ȃ��B
�]���āA�P��ڂɌ������鐻�i�̌��͂R�ȉ��łȂ���Ȃ�Ȃ��B
- �Q��ڂ̌����ŕs�Ǖi���������Ă����v��7,000�~�ɂȂ邽�߂ɂ́A
�Q��̌�����2,000�~���g���Ă����v��7,000�~�ɂȂ�Ȃ���Ȃ�Ȃ�����A
9,000�~�̔��グ���Ȃ���Ȃ�Ȃ��B
�]���āA�Q��ڂɌ������鐻�i�̌��͂Q�ȉ��łȂ���Ȃ�Ȃ��B
- �R��ڂ̌����ŕs�Ǖi���������Ă����v��7,000�~�ɂȂ邽�߂ɂ́A
�R��̌�����3,000�~���g���Ă����v��7,000�~�ɂȂ�Ȃ���Ȃ�Ȃ�����A
10,000�~�̔��グ���Ȃ���Ȃ�Ȃ��B
�]���āA�P��ڂɌ������鐻�i�̌��͂P�łȂ���Ȃ�Ȃ��B
- �S��ڂ̌���������A���v��7,000�~�ɂ��邱�Ƃ͂ł��Ȃ��B
- �Ƃ��낪�A��L�̏����łR��ڂ܂łɂP�P�̐��i�S�����������邱�Ƃ͏o���Ȃ�����A
���ǖ��̕��@�ł͗��v��7,000�~�ɂ��邱�Ƃ͂ł��Ȃ����ƂɂȂ�B
�m�R]�@�@�]���āA�����闘�v�̍ő�z��6,000�~�Ƃ������ƂɂȂ�B
���v��6,000�~�ɂ��邽�߂ɂ́A�P�̏����ɏ]���Č��߂�悢���A
�Ō�Ɏc�������̂͌���������K�v���Ȃ�����A�S��ڂ܂Ŏ��̖����ׂ�悢�B
�S��ڂŕs�Ǖi���o��A�c���Ă���P�͔���邩��A�S����10,000�~�̔���グ������A
���v��6,000�~�ɂȂ邵�A�S��ڂ܂ł̌����ŕs�Ǖi���o�Ȃ��ꍇ�͎c��̂P���s�Ǖi�ƂȂ�A
�ǂ���ɂ��Ă����v��6,000�~�ɂȂ�B
�Ȃ��A�R��ڂ܂ł̌������炷�i���Ƃ��P��ڂ̌����R�ɂ���Ƃ��A�Q��ڂ̌����Q�ɂ���Ȃǁj�ƁA���炵�������T��ڂɎ����Ă��Ȃ���Ȃ�Ȃ��Ȃ邪�A�T��ڂ̌����P�ȏ�ɂ���ƁA�S��ڂ܂łɕs�Ǖi���o�Ȃ������ꍇ�̗��v��
6,000�~�ɂȂ�Ȃ��Ȃ邩��A�����͎��̈�ʂ�Ɍ��܂�Ǝv���܂����A���M�Ȃ��B
�@�@�@�P��ځ@�S��
�@�@�@�Q��ځ@�R��
�@�@�@�R��ځ@�Q��
�@�@�@�S��ځ@�P��
�E����6
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
�S���R���Q���P�̏��Ɍ������܂��B
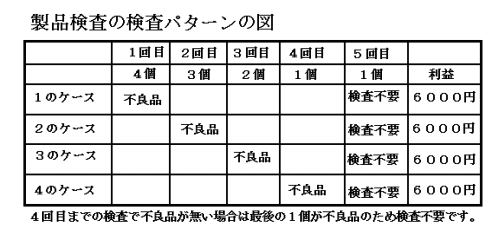
����ڂ̌����ŕs�Ǖi���������Ă�����܂ł̌�����p�������ƂU�O�O�O�~�̗��v�ɂȂ�܂��B
�P�̃p�^�[����
�P��ڂŕs�Ǖi�����������̂Ŏc��̌����͕K�v����܂���B
�]���āA�P�P�O�O�O�|�P�O�O�O�~�i������p�j�\�S�O�O�O�~�i����Ȃ����i�j���U�O�O�O�~�i���v�j
�Q�p�^�[���͂Q��ڂɌ��������̂łP�P�O�O�O�~�\�Q�O�O�O�~�i������p�j
�\�R�O�O�O�~�i����Ȃ����i�j���U�O�O�O�~(���v)
�R�p�^�[���͂R��ڂɌ��������̂łP�P�O�O�O�~�\�R�O�O�O�~�i������p�j�|�Q�O�O�O�~�i����Ȃ����i�j���U�O�O�O�~(���v)
�S�p�^�[���͂S��ڂɌ��������̂łP�P�O�O�O�~�\�S�O�O�O�~�i������p�j�|�P�O�O�O�~�i����Ȃ����i�j���U�O�O�O�~(���v)
�S�p�^�[���܂łɕs�Ǖi��������Ȃ��ꍇ�͍ΈȌ�̐��i���s�Ǖi�ł��B
���̏ꍇ�́A�P�P�O�O�O�~�\�S�O�O�O�~�i������p�j�|�P�O�O�O�~�i����Ȃ����i�j��
�U�O�O�O�~�i���v�j�ƂȂ�܂��B
�E����7
�i�y���l�|���F�]�ʔ����j
�����闘�v�����߂邽�߂ɂ͌��������炷�K�v������A�P�P�̐��i���̃O���[�v�ɕ����Č�������B
�����i�K�ł́A�����ΏۃO���[�v�Ɣ��ΏۃO���[�v�ɁA��ɓ���邱�Ƃ��l����ƁA�ȉ��̂悤�ȃt���[��
���i�����̍H����\�����Ƃ��ł���B
�Ȃ��A�s�Ǖi�����������ꍇ�̗��v������}���邽�߂ɁA��菭�Ȃ����i���̃O���[�v�̌������L���ł���B
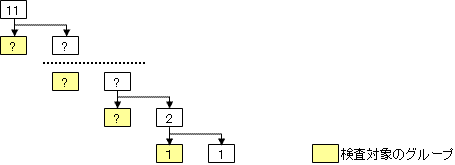
�ŏI�̌����H������t�Z���āA��菭�Ȃ����i���̃O���[�v����������H����g�ނƃP�[�X�T���l�����邪�A
�ő�A�T��̌�����K�v�Ƃ��A����ȏ㌟�������炷���Ƃ͂ł��Ȃ��B
�e�H���ŕs�Ǖi���������ꂽ�ꍇ�̗��v�L���Ă��邪�A�ł��^�������Ƃ��ɓ����闘�v��5000�~�ł���B
���̃P�[�X�̑��ɁA�r���H���ɂ����Đ��i���̑g�������������l�����邪�A���_�͕ς��Ȃ��B
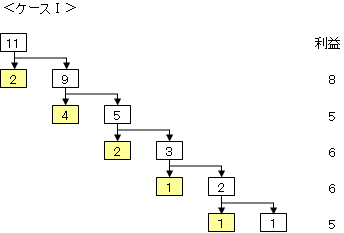
���ɁA�����Ώۂ̐��i������Ώۂ̐��i���Ɠ����܂Ŋ܂߂čl���A�������ő�ł��S��Ɍ��炷�ƁA �P�[�X�U�A�V�A�W�A�X���l������B
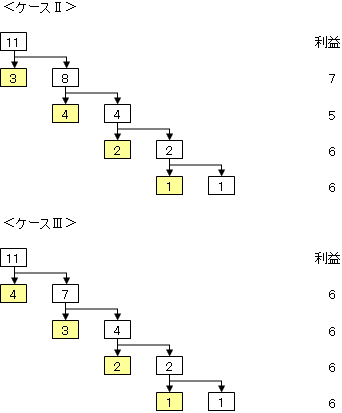
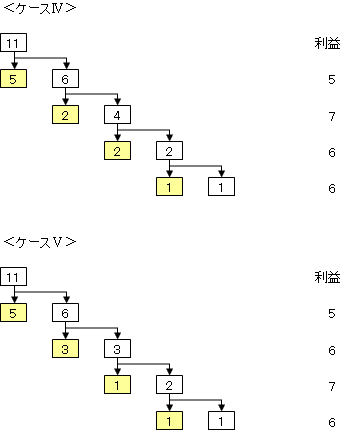
����āA��ӂ����������@�̓P�[�X�V�B���̎��̗��v��6000�~�ł���B
�E����8
�i�y���l�|���Fhaya�j
�őP�̌������@�́A
�@�@4 �� 3 �� 2 �� 1
�Ɣ����o���Č������邱�ƁB�@���ꂾ�ƍň��ł� \6,000 �̗��v�ƂȂ�B
�y�������z
�����ɉ����v�Z���āA
1.. ���������点�Ύ����o����������邩����̌������𑝂₷
2.. �������𑝂₷�� High Return ������ High Risk �ɂȂ�
3.. �傫�����������Ɏ��s����
�Ɨǂ������ƌ�����B�@�K���Ȓ��ԓI�Ȍ��ɕ������Č����������ɍő嗘�v���\�z����A�A���A
�@�@4 �� 3 �� 2 �� 1
���ł��L�͂����ł����B
10�̗ǔۂ�������Ύc���1�̗ǔۂ͎����ł�����A
�a��10�ƂȂ鐮���̑g�̃p�^�[�����~���ɖԗ����ĕ\�ɓZ�߂����̂����}�ł��B
�����̌r���Ɉ͂܂ꂽ�������̃p�^�[���ɑ��āA�E���̐��l�͍����̓��ʒu�ŕs�ǂ������������̋��z�ł��B
�E���̘g�O�ɂ��鐔�l�͍Ō��11�ڂ��s�ǂ������ꍇ�̋��z�ł��B
��ԍ���Min��ɂ��̍s�̋��z�̍ŏ��l��\�������܂������A����� 4 �� 3 �� 2
�� 1 �Ɣ�������Č�������̂��x�X�g�ŁA�ň��ł� \6,000 ���ƕ�����܂��B

�O�̂��߁@Excel �̃}�N���ŁA�~���̕��т����āA�����S 512 �g�̔����o�������`�F�b�N���܂������A���ʂ͓����ł����B
�E����9
�i�y���l�|���FMVH�j
���_����q�ׂ�ƁA
�u�P��ڂS�A�Q��ڂR�A�R��ڂQ�A�S��ڂP�̏��Œ��ׂ�ƁA
�q�ł��^�̈����Ƃ��r�ł��U�O�O�O�~�̗��v��������v
�V�O�O�O�~�̗��v�邱�Ƃ��o���Ȃ����Ƃ��������B
b ��ڂ̌����� a �̐��i�ׂ�Ƃ���Ƃ��A�q�ł��^�̈����Ƃ��r�ł��V�O�O�O�~�̗��v�������邽�߂ɂ́A���̐����̑g (a,b) �͎������K�v������B
�@�@�@(11-a)�~1000-b�~1000 �� 7000
�@�́@a+b �� 4
�@�� (a,b) = (1,1) , (2,1) , (3,1) , (1,2) , (2,2) , (1,3)
�e b = 1,2,3 �ɑ��� a �̍ő�l�̘a�́A 3+2+1=6 �� 11-1=10 �����ł���B����́A�ǂ̂悤�Ȓ��ו������Ă��i�V�O�O�O�~��悤�őP��s�����Ă��j�A���ׂ��Ȃ����i���c�邱�Ƃ�\���Ă���B
����āA�u�q�ł��^�̈����Ƃ��r�ł��V�O�O�O�~�̗��v��������悤�Ȓ��ו��v�͑��݂��Ȃ��B
�Ƃ���ŁA�P��ڂS�A�Q��ڂR�A�R��ڂQ�A�S��ڂP�̏��Œ��ׂ�ƁA
�q�ł��^�̈����Ƃ��r�ł��U�O�O�O�~�̗��v��������i�e�ՂɊm���߂���j�B
�]���āA�`���̌��_��B
�E����10
�i�y���l�|���F��ӂ����̂炢��������j
�T�@�� �ł� �^�������Ƃ������u���̒��ו��ŁA���v����ԏ��Ȃ��Ƃ��v�ƍl���邱�Ƃɂ��܂��B
�Ⴆ�A�P�����i�ׂ�ꍇ���ł��^�������Ƃ����́A
�u�P�O��ڂɕs�Ǖi��������Ƃ��A�܂��͂P�O��ڂ܂łŕs�Ǖi��������Ȃ��Ƃ��v�ł��B
| ������ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ������Ȃ� |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ���v | 9,000 | 8,000 | 7,000 | 6,000 | 5,000 | 4,000 | 3,000 | 2,000 | 1,000 | 0 | 0 |
�E�����̔�p�������ނ̂ŁA�u�����̉������Ƃ��v�����^�������Ƃ����Ƃ����܂��B
�E�����̐��i�ׂ�ꍇ�́A����Ȃ����i�������Ȃ�̂��u�ő�̌��̌����̂Ƃ��ɕs�Ǖi��������Ƃ��v�����^�������Ƃ����Ƃ����܂��B
�U�@���ɋ�̓I�Ȍ������@���l���Ă����܂��B
(1)���i�ׂ�Ƃ��A�Ō�ɂP�c���悤�Ɍv�悷��̂��ǂ��B
����������̂́A�܂��s�Ǖi����������Ă��Ȃ�����ł��B
�c�萻�i�̒��ɕK���s�Ǖi������܂��B
������A�Ō�Ɏc�������i�S������������ƁA���̑S��������Ȃ��Ȃ��Ă��܂��܂��B
�����ŁA�v��́A�Ō�ɂP�c���Č�������̂��ǂ����ƂɂȂ�܂��B�i���̗�Ŋm�F�ł��܂��j
�E�c���Ȃ��Ƃ�
| ������ | 1 | 2 | 3 |
|---|---|---|---|
| ������ | 5 | 3 | 3 |
| ���v | 5,000 | 6,000 | 5,000 |
�E�P�c���Ƃ�
| ������ | 1 | 2 | 3 | ������Ȃ� |
|---|---|---|---|---|
| ������ | 5 | 3 | 2 | �@ |
| ���v | 5,000 | 6,000 | 6,000 | 7,000 |
(2)���i�ׂ�Ƃ��A�����̌����P������悤�Ɍv�悷��̂��ǂ��B
�����̉��P�����Ƃ�1,000�~��p��������܂��B
1,000�~�͐��i�P���̗��v�ł��B
������A���i�ނɂ�āA�����̌����P������悤�ɂ��Ă����ƁA�ǂ̉ŕs�Ǖi���������Ă����v�ɍ����Ȃ��Ȃ�܂��B
�V�@���̖��ł́A���ł��^�̈����Ƃ����̗��v����ԍ������邱�Ƃ��l���Ă��܂��B
������A�����̌v��́A���i�ނƂ������̌����O���葽���͂Ȃ�Ȃ��悤�ɂ��܂��B
�Ⴆ�A�����̉S�̌v�������Ă݂܂��B
�S��̗���l����̂́A�����̌����P�������Ă����悤�Ɂi4�3�2�1�j�v��ł��邩��ł��B
���̕\��No6�͕s�Ǖi�����������ɂ�����炸���v�����ł��邱�Ƃ�������܂��B
�܂��A���̕\���番���邱�ƂŖʔ����̂́A���v�̊��Ғl��No9�̂Ƃ����ő傾�Ƃ������Ƃł��B
| No | �����̌� | �s�Ǖi���܂܂����Ƃ̗��v | ���v�̊��Ғl | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| �P��� | �Q��� | �R��� | �S��� | �P��� | �Q��� | �R��� | �S��� | �c��s�Ǖi | ||
| 1 | 7 | 1 | 1 | 1 | 3,000 | 8,000 | 7,000 | 6,000 | 6,000 | 4364 |
| 2 | 6 | 2 | 1 | 1 | 4,000 | 7,000 | 7,000 | 6,000 | 6,000 | 5182 |
| 3 | 5 | 3 | 1 | 1 | 5,000 | 6,000 | 7,000 | 6,000 | 6,000 | 5636 |
| 4 | 5 | 2 | 2 | 1 | 5,000 | 7,000 | 6,000 | 6,000 | 6,000 | 5727 |
| 5 | 4 | 4 | 1 | 1 | 6,000 | 5,000 | 7,000 | 6,000 | 6,000 | 5727 |
| 6 | 4 | 3 | 2 | 1 | 6,000 | 6,000 | 6,000 | 6,000 | 6,000 | 6000 |
| 7 | 4 | 2 | 2 | 2 | 6,000 | 7,000 | 6,000 | 5,000 | 6,000 | 6000 |
| 8 | 3 | 3 | 3 | 1 | 7,000 | 6,000 | 5,000 | 6,000 | 6,000 | 6000 |
| 9 | 3 | 3 | 2 | 2 | 7,000 | 6,000 | 6,000 | 5,000 | 6,000 | 6091 |
�W�@�V��No6�̒��ו������ł��^�������Ƃ����̗��v����ԍ����Ƃ��ł��邱�Ƃ̊m�F�����܂��B
6,000�~���ڈ��ɂȂ�܂��B
���̂��߂ɁA���ł��^�������Ƃ����̗��v�́A�C�ӂ̂Ƃ��̗��v�ȉ��ɂȂ邱��
�܂��Ă����܂��B
�i�l���₷���Ƃ��̗��v���l����A���̒l�Ł��ł��^�������Ƃ����̗��v�����������܂��j
(1)�����̉��T��ȏ�̌v��ł́A���ł��^�������Ƃ����̗��v��5,000�~���܂���B
�T��ڂɂP�̌��������ĕs�Ǖi�����������Ƃ���ƁA10,000�|5�~1,000��5,000�ɂȂ邩��ł��B
������A�������T��ȏ�̒��ו��͏Ȃ��܂��B
(2)��x�ɂS�ȏ������������@�ł́��ł��^�������Ƃ����̗��v��6,000�~���܂���B
�P��ڂɂS�̌��������ĕs�Ǖi�����������Ƃ���ƁA7,000�|1,000��6,000�ł��B
������A�P��ڂ̌����̌��͂S�ȉ��ɂ���K�v������܂��B
����͂Q��ڂɊ��Z����ƂR�ȉ��A�R��ڂɊ��Z����ƂQ�ȉ��A�S��ڂɊ��Z����ƂP�ȉ��ɂȂ�܂��B�i�����Q��ڂɂS�̌��������ĕs�Ǖi��������ƁA7,000�|2�~1,000��5,000�j
���̂��Ƃ���A�����̉��R��ȉ��̌v����Ȃ����Ƃ��ł��܂��B
�Ȃ��Ȃ�A�Ȃ�ׂ������ȂR�̐����Řa��10�ɂ���ƁA4+3+3 ��10�ł��B
�R��̌v��ł́A�o4,3,3�p���ǂ����ׂĂ��ǂ�������̊��Z�l�ȓ��ɂ����܂�܂���B
�ȏォ��S��̌������c��܂��B
�S��̌����ʼni�ނɂ�Č��������Ȃ����ו��͇V�̕\�ł�����Ă��܂��B
�ȏォ��A�S�A�R�A�Q�A�P�̏��ɒ��ׂĂ����̂����ł��^�������Ƃ����̗��v����ԍ����Ȃ�����ŁA���̗��v��6,000�~�ł��B
�E����11
�i�y���l�|���Fteki�j
�P��ځF�S�A�Q��ځF�R�A�R��ځF�Q�A�S��ځF�P����������B
���̏ꍇ�̍ň��P�[�X�i�ň��ƌĂԂׂ��P�[�X�͂���܂��j�ɓ����闘�v�͂U�C�O�O�O�~�B
���l������
�@�ň��P�[�X��z�肷��ꍇ�A���X�N���ł�����蕽��������K�v������܂��B
�@���̏ꍇ�̃��X�N�́A�u�����{�s�Ǖi�����������Ƃ��̌������v�ł��̂�
������ł��邾�����ɕۂ悤�Ȍ������@���l���܂����B
�@����ɁA���v���ň��̏ꍇ�ł��V�C�O�O�O�~�ƂȂ�悤�ɂ���ɂ́A�ŏ��̌��������R�ȉ��A�Q��ڂ�
�Q�ȉ��E�E�E�E�E�ɂ���K�v������A���ꂾ�ƁA�U�ōs���l�܂��Ă��܂��܂��B�i�܂�����V�ȉ��Ȃ�
�ł��܂����j
�@��ʓI�ɂ́A����������Ƃ���ƁA�����{�P�̐��i������ꍇ�A���̂悤�Ȍ������@���P�ʂ��
���܂�܂��ˁB�i����ȊO�̏ꍇ�́A�����ʂ�̌������@������܂��B�j
������
| �X���[�N�}�� | teki | ��ӂ����̂炢�������� |
| ���q�̗Y�L | �̂����� | haya |
| ykak | �]�ʔ��� | ��̂������� |
| MVH | �I���W |
�R�����g
����́A�����������������Ȃ������̂ł����A
��������ł��傤���B
�S�A�R�A�Q�A�P�Ƃ݂Ă����̂������I�ł����A
���̏ꍇ�A�Ō�̂P�͊m�F����K�v������܂���ˁB
�̂���������̉́A�S�A�R�A�Q�A�Q�Ƃ���܂����A
���̏ꍇ���Ō�̂Q�̎�O�܂ŕs�Ǖi���o�Ȃ��ꍇ�A�c��Q�̒��ɕK���s�Ǖi������킯�ŁA
����͊m�F����K�v�͂Ȃ��A���̏ꍇ���A6,000�~�̗��v���ۏ���܂��B
�������̃R�}�吔�w����
����S���҂���A�₢���킹������܂����B
���̖�肪���グ���邩������܂���!!
���@12��13��25��10������A�������ꂽ�Ƃ̂��Ƃł����A�c�O�A�������Ă��܂��܂����B
 top
top