Challenge!

問題164　数列の和

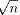　に最も近い整数を　ａ_ｎ　で表す。 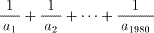　　を求めてください。

---

問題の出典

ジュニア数学オリンピック2003-2008
数学オリンピック財団編
日本評論社

答えと解説

解答・その1

（ペンネ−ム：浜田　明巳）

分数計算が出来るソフトUBASICを使ってみました。答は８８です。
掃き出したデータを見てみると，ａ_n＝ｍとなるｎにおいて， １／ａ_n＝１／ｍをすべて足し合わせてみると，整数になる事が分かります．

   10   'asave "wm1008.ub"
   20   open "wm1008.dat" for output as #1
   30   Wa=0
   40   for N=1 to 1980
   50     A1=sqrt(N)
   60     A2=int(A1+0.5)
   70     Wa+=1//A2
   80     print N;A1;A2;Wa
   90     print #1,N;A1;A2;Wa
  100   next N
  110   close #1
  120   end

---

解答・その2

（ペンネ−ム：エルドス）

basicで組んでみました。ｓ＝87.9999999999923となり、答えは８８のようです。
参考までに足す順番を逆にして1980から1まで順に足していくとｓ＝87.9999999999938 になるので、
下二桁ぐらいは誤差の内としても差し障りがないと判断すべきでしょう。

  
  CLEAR 
FOR n=1 TO 1980
   LET p=n^0.5-INT(n^0.5)
   IF p>0.5 THEN LET a=INT(n^0.5)+1
   IF p<=0.5 THEN LET a=INT (n^0.5)
   LET s=s+1/a
NEXT n
PRINT s
END

---

解答・その3

（ペンネ−ム：杖のおじさん）

１/√１９８０＝1/４４．４９７１９０９２・・・＝条件により→1/４４
１/√１９８１＝1/４４・５０８４２６１７・・・＝条件により→1/４５

数列で考えると
　　1/√１＝1/1 ＋1/√2=1/1＝２
　　1/√３＝1/2 ＋ 1/√4＝1/2 ＋ 1/√5＝1/2＋ 1/√6＝1/2＝２
　　1/√７= 1/3 ＋1/√８=1/3 ＋ 1/√９=1/3 ＋1/√10＝1/3 ＋1/√11=1/3＋ 1/√12=1/3=２
　 　 ・
　　　 ・
　　 　・
1/√1980=1/44であり各項が２なので、４４×２＝８８が答えです。

ＣＡＳＩＯ　ＦＸ−８７０Ｐ　のポケットコンピュータで計算しました。
プログラムは次のように作りました。

１０．ＰＲＩＮＴ“セイスウ ノ ワ＝”：Ａ＝０：Ｔ＝０
２０．ＦＯＲ　Ｎ＝１　ＴＯ　１９８０
３０．Ａ＝１/ＩＮＴ（ＳＱＲ N＋０．５）
４０．Ｔ＝Ｔ＋Ａ
５０．ＮＥＸＴ　Ｎ
６０．ＢＥＥＰ
７０．ＰＲＩＮＴ“コタエ　ハ＝”；Ｔ
８０．ＩＦ　ＩＮＫＥＹ＄＝“”８０ＴＨＥＮ　８０
９０．ＧＯＴＯ　１０

このプログラムを実行するとコタエ　ハ＝８７．９９９９９９９８と表示されます。
これは１９８０個の分数を加算した事になるから８８にはならなかったのです。
　　√１９８０＝44.49719092=44
　　√１９８１＝44.50842617=45
上記の検証により√１９８０が４４の最後の整数であることも分かりました。
従って４４項目は４４個の分数がありその項の和は２である事が分かります。

従って答えは４４×２＝８８です。

---

解答・その4

（ペンネ−ム：falcon@中学教師）

＜答え＞
88

＜考え方＞
ａ_ｎの移り変わりですが、
　１，１，
　２，２，２，２，
　３，３，３，３，３，３，
　４，４，４，４，４，４，４，４，
　・
　・
　・
というように、同じ数字の個数が2個、4個、6個、8個･･･と2個ずつ増えていきます。
このことから与式において、ａ_ｎ が同じ数字になる項の部分の和はそれぞれ全て２になります。
与式の中に、この和が２になる項の部分はちょうど44組あるので、与式の答えは８８。

---

解答・その5

（ペンネ−ム：teki）

さて、今月の問題ですが、すでに問題１３３で数値は違うものの、出題されてます。
というわけで、今回は、答えだけ送信しておきます。
答え　　８８

---

解答・その6

（ペンネ−ム：転位反応）

題意に従って、ｎ、ｎ ^1/2、 ａ_n　を具体的に書き出してみると、 以下の通りであり、同じ値を取るａ_nの個数は２ａ_nと予想される。

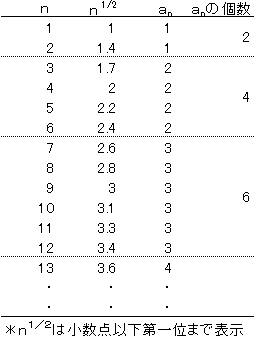
そこで、一般的にａ_nの個数を求めてみる。
ｎ^1/2の取り得る範囲は
　　　ａ_n−１／２　≦　ｎ^1/2　＜ａ_n＋１／２
二乗して、
　　　ａ_n^２−ａ_n＋１／４　≦　ｎ　＜　ａ_n^２＋ａ_n＋１／４
ｎは整数であることから、
　　　ａ_n^２−ａ_n＋１　≦　ｎ　≦　ａ_n^２＋ａ_n
この範囲に含まれるａ_nの個数は
　　　（ａ_n^２＋ａ_n）-（ａ_n^２−ａ_n＋１）+1＝２ａ_n
再度、表を整理すると以下の通り。

これらの結果を与式に代入して
与式=２（１／１）＋４（１／２）＋６（１／３）＋・・・＋８８（１／４４）
　　=２＋２＋２＋・・・＋２
　　=２×４４
　　=８８

---

解答・その7

（ペンネ−ム：スモークマン）

m+1/2＜√n＜(m+1)+1/2
m²+m+1/4＜n＜m²+3m+9/4
m²+m+1≦n≦m²+3m+2　　…√n=m+1
m²+3m+2-(m²+m)=2m+2=2(m+1) 個
m(m+1)+1　〜　(m+1)(m+2)

m-1+1/2≦√n≦m+1/2
m²-m+1/4≦n≦m²+m+1/4
m²-m+1≦n≦m²+m　　…√n=m
(m-1)m+1　〜　m(m+1)
m²+m-(m²-m)=2m個

　　1980=44*45♪
つまり…
　　1…2個
　　1/2…4
　　1/3…6
　　1/4…8
　　…
　　1/44…88
それぞれの和はすべて 2
よって…合計=2*44=88
でいいのかな...^^?...

もっとスマートに言えないかなぁ…^^;?...

---

解答・その8

（ペンネ−ム：オヤジ）

[　]：Ｇauss記号とすると　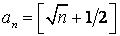　となる

a_１〜a_２＝１：２個
a_３〜a_６＝２：４個
a_７〜a_１２＝３：６個
a_１３〜a_２０＝４：８個
・・・・・・・・・・・
・・・・・・・・・・・
a_１８０７〜a_１８９２＝４３：８６個
a_１８９３〜a_１９８０＝４４：８８個

以上により　a_ｎ＝ｍ　となる　a_ｎの個数は、２ｍ個となる

よって1/a₁+1/a₂＋・・　　・・+1/a₁₉₈₀　＝２×４４＝８８

　∴　８８

---

解答・その9

（ペンネ−ム：T_Tatekawa）

n の平方根ではなく，a_n² を考えます．

1.5² = 2.25,　 2.5² = 6.25, 　3.5² = 12.25 なので，
　　a₁ = a₂ = 1
　　a₃ = a₄ = a₅ = a₆ = 2
　　a₇ = .... = a₁₂ = 3
となります． この考え方をちょっと拡張します．

k を整数として，k の平方根に最も近い整数の個数を考えます．

　　(k+0.5)² - (k-0.5)²
　= (k² + k + 0.25) - (k²2 - k +0.25)
　= 2k

になります． k=1, 2, 3 の場合に当てはめると，上記と一致します．

　　44.5 * 44.5= 40² + 2 * 40 * 4.5 + 20.25 =1980.25

なので，a₁₉₈₀ = 44 です． a₁₉₈₁ = 45 となります．

a_n が k となるものが 2k 個あるので，求める和は

　1/1 * (2*1) + 1/2 * (2*2) + ... + 1/44 * (2*44)
　= 2 * 44
　= 88

です．

---

解答・その10

（ペンネ−ム：シュレーディンガーの三毛猫）

答：88

＜解法＞
題意より、ｎを自然数とし、便宜上、数列a_nをa(n)と書く。
√ｎは単調増加かつ正なのでa(n+1)≧a(n)＞0である。
また、任意のa(n)の値に対してa(n)²=nとなるｎが存在する。
よって、n(n=1,2,3,4,・・・)について数列a(n)は
1から順に全ての自然数の値をとりながら増加するので、
　　a(n)=1,1,・・・・1,2,2・・・2,3,3,・・・
という形をしている。
そこでまず、あるa(n)の値をとるnの個数を求め、a(n)の形を決定する。
a(n)とnとの間には
　　a(n)-0.5＜√n＜a(n)+0.5
の関係がある。辺々2乗して、
　　a(n)²-a(n)+0.25＜n＜a(n)²+a(n)+0.25
となるので、あるa(n)の値をとるnの個数は
　　[a(n)²+a(n)+0.25]-[a(n)²-a(n)+0.25]=2a(n)
と求められる。
例えば、a(n)=1となるnの個数は2個、a(n)=2の時は4個である。

n=1の時、a(1)=√1=1なので、
数列a(n)はn(n=1,2,3,4・・・・)に対して
　　a(n)=1,1,2,2,2,2,3,3,3,3,3,3,4・・・・
となる。

次に、n=1980の値を求め、最終的な解を求める。
あるa(n)の値をとるnの個数は2a(n)個であったので、mを自然数とすると、 n=1から数えて、(m-1)m+1番目からm(m+1)番目までがa(n)=mとなるnの範囲である。
(ここで、自然数NについてN=1からN=mまでの2Nの和がm(m+1)であることを用いた。)
さて、1980=44×45なので、これはm=44の時に相当し、a(1980)=44である。
また、n=1980がa(n)=44の値をとる最大のnであり、 a(n)=44を満たすnの個数は2×a(n)=2×44=88個であることが判る。

以上より、
　　1/a(1)＋1/a(2)＋1/a(3)+1/a(4)+1/a(5)+1/a(6)+・・・+1/a(1893)+・・・+1/a(1980)
　　=(1/1＋1/1)＋(1/2+1/2+1/2+1/2)+・・・+(1/44+・・・・+1/44)
　　=2×(1/1)＋4×(1/2)+・・・+88×(1/44)
　　=2×44
　　=88
を解として得る。

---

解答・その11

（ペンネ−ム：SOU）

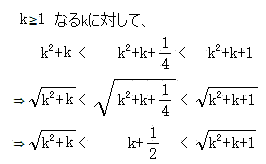
が云えるので、



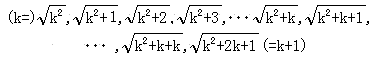
のうち、k と k+1/2 の間にある数は



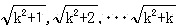
のk個、k+1/2 と　k+1 の間にある数も



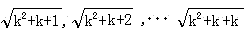
のk個になることがわかる。すると、a_n は



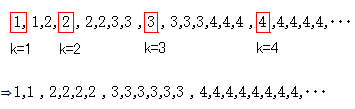
という並び方をすることがわかる。 したがってこれらの逆数を考えると、同じ値のgroupの和は常に2なので、



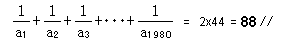
となる

---

解答・その12

（ペンネ−ム：AND）

答えは２X４４＝８８となります。
√ｎ　に最も近い整数を　A（ｎ）　で表す。
A(ｎ）は、以下のように同一の値αが暫く続き、α＋１が暫く続くという数列になります。

ｎ	１	２	３	４	５	６	７	８	９	・・・・
A（ｎ）	１	１	２	２	２	２	３	３	３	・・・・

そこで、まず同一の値 A(ｎ）＝αが何回連続するのかを求めることにします。
√ｎが以下の範囲にある場合、A(n)は同一の値αを持ちます。
　　　α-0.5 ≦ √ｎ ＜ α-0.5　（αは整数）
上記の式を２乗すると以下のとおりとなります。
　　　α^２-α＋0.25　≦ ｎ ＜ α^２+α+0.25
定義よりｎは整数ですから、0.25の部分を消去して、以下の式を得ます。
　　　α^２-α　＜　ｎ　≦　α^２+α
従って、A(n)＝αが連続する回数は、２α回となります。
求める演算は、1／A(1)　＋　1／A(2)　＋　・・・・　＋１／A(1980)ですから、
　１／１×（１ｘ２）　＋　1／２×（２×２）　＋　・・・・　＋１／ｎ×（２ｘｎ）＋・・・１÷A(1980)
＝２＋２＋　・・・・　＋２＋・・・＋１／A(1980)
ここで、√１９８０は、４４．４９７.... で、√１９８１は４４．５....ですから、
A(１９８０）＝４４で、A(1981)＝４５となるため、１／４４が８８回連続する最大のｎであることが分かります。
故に、答えは２X４４＝８８となります。

---

解答・その13

（ペンネ−ム：ykak）

答え　８８

考え方
１から１８９０までの整数を分母とし、分子を１とする次のような分数の列を考える。
　　　1/1, 1/2, 1/3, 1/4, . . . . . . . . 1/1890
問題の左辺は、この分数のそれぞれの分母をA_n（aを大文字で書きます）で置き換えたも のを加えたものだから、問題の左辺の各項と上の数列の各項は１対１に対応する。

上の分数列で、分母が平方数になっているもの（仮に1/m²とする）に注目する。1/m² の左側にある項で分母が平方数になる一番近い項は1/(m-1)²、右側にある項で分母が 平方数になる一番近い項は、1/(m+1)²である。
上の３つの項を左から順番に、X｛=1/(m-1)²｝　Y｛=（1/m²)｝,　Z｛=1/(m+1)²｝とする。
上の分数列でXY間にはいくつの項があるかを見ると、分母が整数の並びであるから m² - (m-1)² - 1 で、2（m - 1）個の項があることになる。
同様に、YZ間には、(m+1)² - m² - 1 で、2m 個の項があることが分かる。
次にYからZまでの分数列の分母の平方根を取った数字の列を考える。

　　

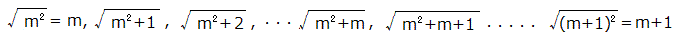
これらの数字が数直線上に並んでいると考えて、両端の点の中点にあたる √(m²) + 1/2　 との大小関係を見ると、Yから m 番目の √(m²+m) までは √(m²) + 1/2 より小さく、 m+1 番目から右の項はこれより大きい、つまりYの右側には分母が次の平方数になるZまでの間に 2m 個の項があり、そのうちの左から半分の m個はその分母の平方根が √(m²) + 1/2 より小さく、 残りの m個はその分母の平方根が √(m²) + 1/2 より大きい、ということが言える（それぞれ 2 乗して差を取ってみると分かる）。
このことから、YZ間の分数列の分母をA_nに置き換える（これが問題の数列）と、Y点にあたる 項の値は 1/mであるが、これから右側の m 個の項も、A_nは√nに一番近い整数という問題の 条件から、 値が1/m になり、それより右側の m個の項は1/(m+1) になることが分かる。
XY間でも同じことが言え、そのことから、Yの左側の、m-1 個の項の値が 1/m になることが分かる。
従って、問題の数列のうち平方数を分母とするある項（1/m とする）を見ると、その左側の m - 1 個の項は、値が 1/m になり、右側の m個の項も値が 1/m になることが言える。そして、 これらの数を一つのグループと考えて、その和をとると
　　1/m × (m - 1) + 1/m （分母が平方数である自身）+ 1/m × m = 2
となる。
問題の数列のうち、分母が平方数となる項を中心にして上のようなグループを作っていくと、各グ ループは互いに接しており、すべての項を尽くしていることになる。
問題の数列のうち、最初の 1/1 は左側の項がないが、その和は 2 であるから、他のグループと同様に扱ってよい。
1890 より小さい平方数で最大のものは 1936（44²) であるが、問題の数列のうち1/1936 の項の上の意味でのグループのうち、1/1936 より右側にあるものの個数は 44個で、その 44個目は1/1980 になる( 1936 + 44 = 1980 )から、問題の数列の右端は、1936（44²) のグループの右端 と一致している。
従って、答えは、１ から 44 までの上の意味のグループの和を取ればよいということになるが、 1 つのグループの項の和は 2 であるから、答えは、これに 44 をかけた 88 となる。

---

解答・その14

（ペンネ−ム：迷子の雄猫）

以下、ｋは1以上の自然数であるとする。
ルートｎ　に最も近い整数を　ａ（ｎ）であらわす。
ということは、ａ（ｋ^２）＝ｋであり、ａ（（ｋ＋１）^２）＝ｋ＋１であり、 ａ（（ｋ−１）^２）＝ｋ−１である。

（ｋ＋１）^２−ｋ^２−１＝２ｋより、 ｋ^２と（ｋ＋１）^２の間には、自然数が２ｋ個ある。
（ｋ＋１／２）^２＝ｋ^２＋ｋ＋１／４より、 上記２ｋ個の自然数のうち、その二乗根に最も近い整数がｋとなるのはｋ個 その二乗根に最も近い整数が（ｋ＋１）となるのも、やはりｋ個となる。
（ｋ−１）^２とｋ^２の間にも、同様に その二乗根に最も近い整数がｋとなるのは（ｋ−１）個あるので、 全ての自然数のうち、その二乗根に最も近い整数がｋとなるのは その二乗根がｋそのものとなるｋ^２をくわえて （（ｋ−１）＋１＋ｋ）＝２ｋ個ある。

よって題式は１／ｋが２ｋ個並ぶので、 少なくとも途中までは２＋２＋２＋２＋.....という形に整理できる。
１９８０．２５の二乗根は４４．５なので、 ２が４４個並んで余分な項はない。
よって答えは８８．

---

解答・その15

（ペンネ−ム：haya）

数列の和は 88 です。

【解き方】

---

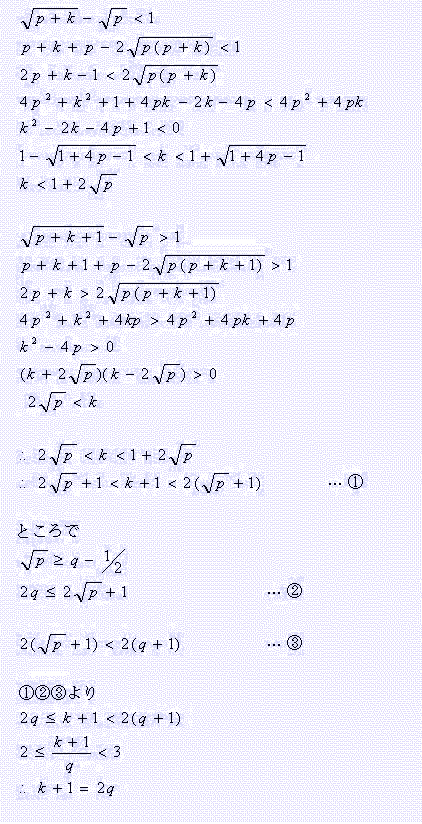
解答・その16

（ペンネ−ム：のっこん）

pを0以上の整数とする（pは何桁の整数でも構わない）

(p+0.5)²=p(p+1)+0.25 ・・・(1)
(p+1+0.5)²=(p+1)(p+2)+0.25 ・・・(2)

(2)-(1)=2(p+1) ←これは(1)が示す数と(2)が示す数との間に整数が何個あるかを表す

p が0の時　2(p+1)=2
　よって(0.5)²より大きく (1.5)²より小さい整数は2個
　この時これらの整数に対応する値はp+1=1

p が1の時　2(p+1)=4
　よって(1.5)²より大きく (2.5)²より小さい整数は4個
　この時これらの整数に対応する値はp+1=2

p が2の時　2(p+1)=6
　よって(2.5)²より大きく (3.5)²より小さい整数は6個
　この時これらの整数に対応する値はp+1=3

　　　・・・・・・・・・・・・・・・

p がkの時　2(p+1)=2(k+1)
　よって(k+0.5)²より大きく(k+1+0.5)²より小さい整数は 2(k+1)個
　この時これらの整数に対応する値はp+1=k+1

√1980=44.497・・・
√1981=44.508・・・だから
1980 は対応する値が44になる最大の整数である
値が44の時、そうなる整数の個数は2・44=88

与式=2・1+4・(1/2)+6・(1/3)+・・・・・+88・(1/44)
　　　=2・44=88

---

解答・その17

（ペンネ−ム：三角定規）

【解答】
正整数 m，n に対し
　　(m−1/2)²≦n＜(m＋1/2)² …(1)
すなわち
　　m²−m＋1/4≦n＜m²＋m＋1/4　…(2)
のとき
　　a_n＝m …(3)
で，このような n は(2)より
　　(m²＋m＋1/4)−(m²−m＋1/4)＝2m
個現れる。 以上より，a_n は，第 m 群が 2m 個の m から成る群数列で，
　　Σ[k=1，44](2m)＝m(m＋1)|m=44＝44・45＝1980
であるから，1980 は第44群の末尾の数である。 よって，
　　1/a₁＋1/a₂＋…＋1/a₁₉₈₀＝(1/1＋1/1)＋…＋(1/44＋…＋1/44)
　　　　　　　　　　　　　　　　　　＝2＋2＋…＋2
　　　　　　　　　　　　　　　　　　＝88　…[答]

---

解答・その18

（ペンネ−ム：MVH）

まず,

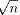　　　=a+0.5　・・・(1)

を満たす自然数の組　(n,a)　が存在する, と仮定する.
このとき, (1)の両辺を２乗して整理すると,

　　n-a²-a=0.25

この左辺は整数で, 右辺は整数でないから, 矛盾. 仮定が矛盾を導いたので, 仮定が誤り. よって, (1)を満たす自然数の組　(n,a)　は存在しない.
さて, (1)を踏まえると, 自然数に対して, 「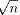　に最も近い整数　a_nが　k　であるような　n　」の個数は,

　　

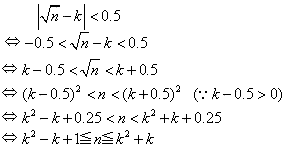
より、

　　(k²+k)−(k²-k+1)+1=2k　（個）

ある.ここで、

　　(k+1)²−(k+1)+1=k²+k+1

であることに注意する.
以上により, a_n=k　を満たす最大の　n　は, 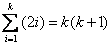で与えられることが分かるから,

　　44×(44+1)=1980

より,n=1980 が「a_n=44を満たす最大のn　」であることが分かる. 従って,

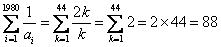　　　　（答え）.

---

解答・その19

（ペンネ−ム：夜ふかしのつらいおじさん）

ａ_nは次の表のような値をとります。

よって、求める数列の値は、

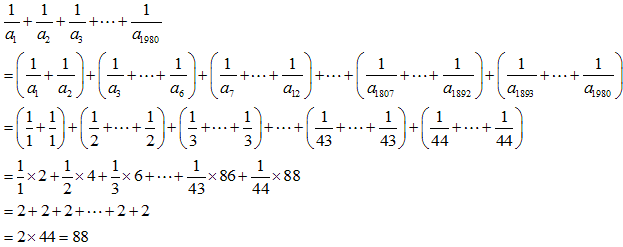
となります。

これは、次のように説明できます。

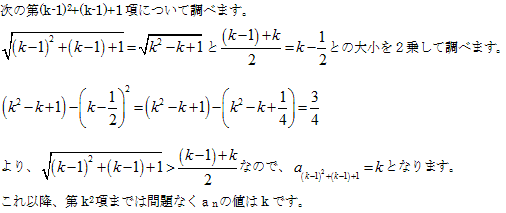
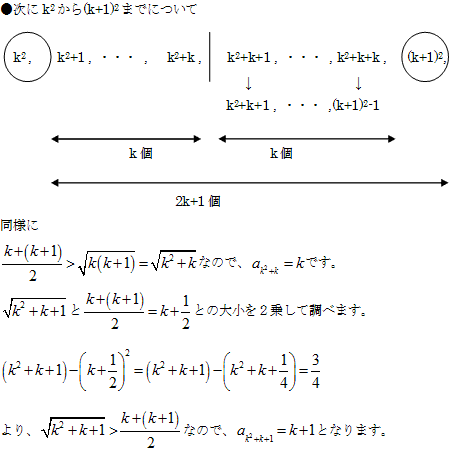
●以上から第k² 項の前後について
・第k² 項の前(k-1)個の項の値は、k
・第k² 項の値はk
・第k² 項の後k 個の項の値はk
合計２ｋ個の項の値がk となります。

正解者

teki	スモークマン	転位反応
夜ふかしのつらいおじさん	オヤジ	浜田　明巳
迷子の雄猫	のっこん	haya
ykak	AND	SOU
falcon@中学教師	エルドス	杖のおじさん
T_Tatekawa	MVH	シュレーディンガーの三毛猫
三角定規

コメント

うっかりして、１３３．２００８年の問題と同じものを提示してしまいました。 申し訳ありませんでした。あえて、前回と違う解答をお寄せいただいた方もいらっしゃいました。感謝です。

---