Challenge!

１３３．２００８年の問題

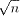に最も近い整数をａ_ｎ で表す。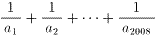を求めよ。

---

問題の出典(改題)

ジュニア数学オリンピック
数学オリンピック財団編
亀書房発行

答えと解説

解答・その1

（ペンネ−ム：オヤジ）

[　]：Ｇａｕｓｓ記号とすると

　　　ａ_ｎ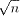＝[＋1/2]　となる

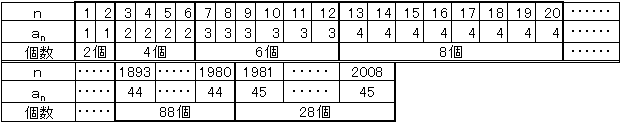
　　ａ_１〜ａ_２　　　　＝１　：２個
　　ａ_３〜ａ_６　　　　＝２　：４個
　　ａ_７〜ａ₁₂　　　　＝３　：６個
　　ａ_１３〜ａ₂₀　　　＝４　：８個

以下同様に
　　ａ_１８９３〜ａ_１９８０＝４４：８８個
また
　　ａ_１９８１〜ａ_２００８＝４５：２８個
以上により
　　　１／ａ_１＋　〜　＋１／ａ_２００８＝２×４４＋２８／４５＝３９８８／４５
∴　３９８８／４５

---

解答・その2

（ペンネ−ム：巷の夢）

題意から以下の表の様にまとめることが出来る。 即ち、1が2個、2が4個、3が6個、4が8個と いう様に各々の整数の2倍個数となる。

ｎ		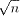最も近い整数
1	1	1
2	1.41	1
3	1.73	2
4	2	2
5	2.23	2
6	2.44	2
7	2.64	3
8	2.82	3
9	3	3
10	3.16	3
11	3.31	3
12	3.46	3
13	3.60	4
14	3.74	4
15	3.87	4
16	4	4
17	4.12	4
18	4.24	4
19	4.35	4
20	4.47	4
21	4.58	5
･･･	･･･	･･･

これより、求めるものは、

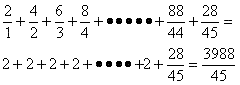
となる。

---

解答・その3

（ペンネ−ム：のっこん）

0.5²＝0.25
1.5²＝2.25
2.5²＝6.25
3.5²＝12.25
・・・・・・・・なので

(1)0.25≦n＜2.25の時、つまり1≦n≦2の時　　a_n＝1
(2)2.25≦n＜6.25の時、つまり3≦n≦6の時　　a_n＝2
(3)6.25≦n＜12.25の時、つまり7≦n≦12の時　　a_n＝3
・・・・・・・・・・・・・・・・・・・・・・・・・・・・

2m（m=1、2、3、・・・）個のnに対し、a_n＝mとなる（証明が必要かなあ）

2+4+6+・・・+2m=2008 とおくと
1+2+3+・・・+m=（1/2）・m・（m+1）=1004
これを解いて m=44.31・・・
2+4+6+・・・・+88=（1/2）・90・44=1980
1981を1番とすると2008は28番目だから

　　　S=(1/1)・2+(1/2)・4+(1/3)・6+・・・+(1/44)・88+(1/45)・28=2・44+(28/45)=3988/45

---

解答・その4

（ペンネ−ム：バルタン星人）

回答：８８と２８／４５

解法
（Ａ₁，Ａ₂，・・・・・・・Ａ₂₀₀₈）は （１，１，２，２，２，２，３，３，３，３，３，３，４・・・４５）
４４の終わりは
　　　２×（１＋２＋・・・４４）＝２×４５×２２＝１９８０
４５は、２００８−１９８０＝２８個ある。
ゆえに逆数の和は
　　　２×４４＋１／４５×２８＝８８と２８／４５

---

解答・その5

（ペンネ−ム：スモークマン）

(k+1/2)²=k²+k+1/4　つまり、
(k²)^1/2≦k≦(k²+k)^1/2=(k(k+1) )^1/2 で、 (k²+k+1)^1/2 は、k+1 に属す。

1〜2 までは、	1・・・1〜1*2
3〜6	2・・・3〜2*3
7〜12	3・・・7〜3*4
・
・
・
1893〜1980	44・・・1893〜44*45=1980
1981〜2008 (〜45*46=2070)	45

2008-1980=28、k(k+1)-(k-1)k=2k なので、、、
　　　2/1+2*2/2+2*3/3+・・・+2*44/44+28/45=2*44+28/45=88+28/45

---

解答・その6

（ペンネ−ム：長崎島原　かがみ）

---

解答・その7

（ペンネ−ム：kiyo）

        1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0,1,2,3,4,5,6,7,8,9,0
A(n)は、1,1,2,2,2,2,3,3,3,3,3,3,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,5,・・・・・・,

　　　n(n+1)＜2008
　　　n=44 44*45=1980
　　　与式=2*44+(1/45)*(2008-1980)=88+28/45=3988/45

答え 3988/45。

---

解答・その8

（ペンネ−ム：庄司）

計算してみて分かった事ですが、a_nの値が等しくなるnの数はa_n*2個存在するようです。
つまりa_n=1はa₁,a₂の2つ、 a_n=2はa₃,a₄,a₅,a₆の4つ、 a_n=3はa₇,a₈,a₉,a₁₀,a₁₁, a₁₂の6つ存在します。
したがって、

　1/a₁+1/a₂+1/a₃+1/a₄ +1/a₅+1/a₆+1/a₇+1/a₈+1/a₉ +1/a₁₀……+1/a₁₂+……
＝(1/a₁+1/a₂)+(1/a₃+1/a₄+1/a₅+1/a₆) +(1/a₇+1/a₈+1/a₉+1/a₁₀……+1/a₁₂)+……
＝(1/1+1/1)+(1/2+1/2+1/2+1/2)+(1/3+1/3+1/3+1/3+1/3+1/3)+……
＝2+2+2+……

となります。 a₂₀₀₈=45ですので、a_n=44となる数までの1/a_nの総和は2*44=88。
a_n=45となるnは、n=1981からn=2008の28個。
よって解は88+28*1/45=88+28

---

解答・その9

（ペンネ−ム：teki）

＜答え＞　　３９８８/４５
ちょっとやってみればすぐに規則性がわかりますが、 与式は

　　　１×２＋1/2×４＋1/3×６＋1/4×８・・・・・1/44×８８＋1/45×２８

となります。つまり、２×４４＋28/45　ですね。 なお、最後の２８は、２００８−�狽S４×２　です。

---

解答・その10

（ペンネ−ム：転位反応）

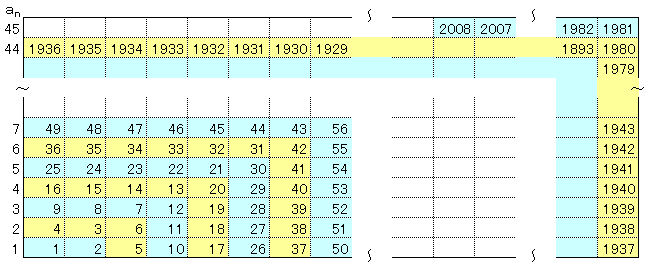
整数nを１から順に平方数が左端に並ぶように整理すると、 題意ａ_ｎを満たす整数ｎは下表のように分類することができる。
例えば、整数ｎ＝７、８、９、１０、１１、１２について、ａ_ｎ＝３なので

　　　１/ａ_７＋１/ａ_８＋１/ａ_９ ＋１/ａ₁₀＋１/ａ₁₁＋１/ａ₁₂＝１/３×６＝２

ａ_ｎ(ｎ＝１〜４４)について、それぞれ逆数の和は２
ａ₄₅については、１/４５×２８
従って求める和は、 ＝2×44＋28/45 ＝88＋28/45

　

---

解答・その11

（ペンネ−ム：杖のおじさん）

答え　８８＋２８／４５です。

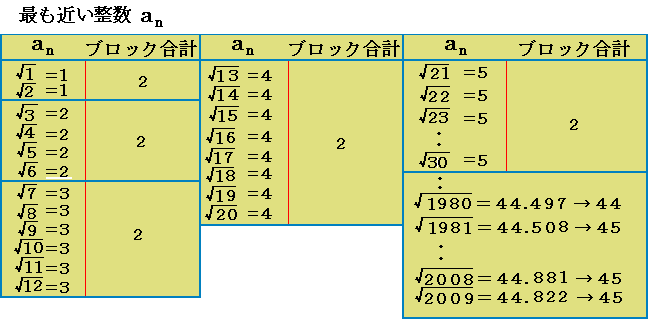
上のように規則性を見てみました。その結果√を開き整数部分に０．５を加算して 端数を切り捨てます。各ブロックの合計は２です。
√２００８の含まれるブロックの項の数は次の通りです。
√２００８＝４４．８１４は４４．８１４＋０．５＝４５．３１４＝４５となります。
√２００９＝４４．８２１で４５となり√２００８は４５ブロックの中間と分かります。
ブロックの各項は１／４５なので
√１９８１から√２００８までの項数は２８なのでその和は１／４５×２８＝２８／４５
従って４４×２＋２８／４５＝８８＋２８／４５です。

---

解答・その12

（ペンネ−ム：ＳＯＵ）

まず、　(n+1)2 - n2 -1 = 2n 
より、　n2 と (n+1)2 との間には整数が 2n 個ある事になります。
つまり、an2 = √(n2) と 
a(n+1)2 = √{(n+1)2} の間に 2n個の数がありますが、
それらの数は題意より n か n+1 のどちらかになります。
どこを基準にその判断を行うのかというと、平方根の正の方をとった時に 
 n+1/2 になるような数、即ち (n+1/2)2 です。
これを展開すると
 n2 + n + 1/4 となり、これは 
 n2 + n と  n2 + n + 1 の間に存在する整数でない数です。
要するに、an2 と a(n+1)2 の間の2n個の数のうち、
はじめのn個 an2+1 〜 an2+n の値は n となり、
その後のn個 an2+n+1 〜 an2+2n  の値はは n+1 になります。
以上のことから、
an={1,1,2,2,2,2,3,3,3,3,3,3,4,4,4,4,4,4,4,4,5,5,5,5,5,5,5,5,5,5,・・・,45,45,45}
のようになります。
法則として m は 2m個続きます。45 だけ 28個あまります。
よって
与式 = Σ(ak)-11≦k≦2008 
     = 2+2+2+・・・2+2+28/45
     = 88+28/45 // 

---

解答・その13

（ペンネ−ム：kohji）

m,nを自然数とする。
　a_n=m
⇔ m-1/2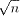＜ ＜m+1/2
⇔ m²-m+1/4＜n＜m²+m+1/4
⇔ m²-m+1≦n≦m²+m
∴a_n=m となるのは　第m²-m+1項から第m²+m項までの2m項。
また、a_nを以下のように分ける。
{a_n}={1,1|2,2,2,2|3,3,3,3,3,3|4,…}　すると
　45²-45+1≦2008≦45²+45
　2008-(2*1+2*2+…+2*44)=2008-44*45=28
なので、a₂₀₀₈は第45群第28項。
よって求める和は、
　2*1*1+2*2*(1/2)+2*3*(1/3)+…+2*44*(1/44)+28*(1/45)
=2*44+28/45
=3988/45

---

解答・その14

（ペンネ−ム：T_Tatekawa）

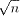に最も近い整数を a_n で表すときは， n に最も近い整数の2乗を a_n² で表すと言い換える事が出来る．
a_n の値が変わる境界は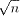， = (2k+1)/2 なので， n = (2k+1)²/4 である．（k は整数）
もし n ＜ (2k+1)²/4 ならば，a_n = k であり， n ＞ (2k+1)²/4 ならば，a_n = k+1 である．
2k+1 は常に奇数なので，(2k+1)²/4 は整数にならない．
次に，a_n = k となる n が幾つあるかを数える．
　　　(2k+1)²/4 - (2(k-1)+1)²/4 = 2k
なので，2k 個である．
最後に a₂₀₀₈ は
　　　(89/2)² = 7921/4 = 1980 + 1/4
なので，a₂₀₀₈=45 である．
つまり，1981 ≦ n ≦ 2008 では a_n=45． a_n=k (k＜45) については各々 2k 個ずつあるので，
　　　　1/a₁ + 1/a₂ + ... + 1/a₂₀₀₈
　　　= 2 x 44 + (2008-1980)/45
　　　= 88 + 28/45

---

解答・その15

（ペンネ−ム：三角定規）

---

解答・その16

（ペンネ−ム：夜ふかしのつらいおじさん）

ｎ²から(ｎ＋１)²までは、自然数が２ｎ＋１個あります。
(ｎ＋１)²−ｎ²＝２ｎ＋１です。

　　　

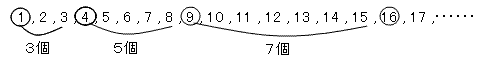
これは平方根をとったとき、整数部分がｎとなる自然数は、２ｎ＋１個あることを示します。
しかし、これは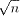 にもっとも近い整数ａ_ｎの個数を与えません。
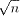にもっとも近い 整数ａ_ｎの個数を数えるためにそれぞれの数の平方根を小数第１位まで求めてみます。

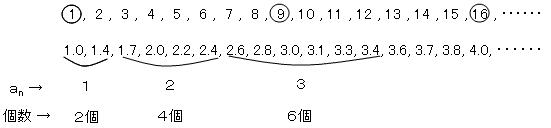
整数ａ_ｎの個数は次の計算で偶数個と分かります。

　　　

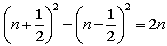
つまり、次のようになっています。

確認は、2+4+6+・・・+88+28＝2×（1+2+3+・・・+44）+28＝44×45+28＝2008
よって、

　　　

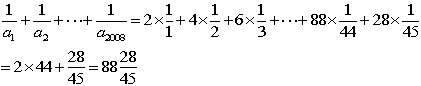
約88.6222・・・となります。

正解者

teki	のっこん	スモークマン
夜ふかしのつらいおじさん	バルタン星人	転位反応
kohji	庄司	kiyo
巷の夢	オヤジ	T_Tatekawa
三角定規	杖のおじさん	長崎島原　かがみ
ＳＯＵ

まとめ

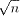に最も近い整数をａ_ｎとすると、ａ_ｎ＝ｋとなるｎの個数は、 ２ｋ個になります。おもしろいですよね。
その様子がわかるようにと、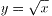のグラフ上に格子点を打ってみました。

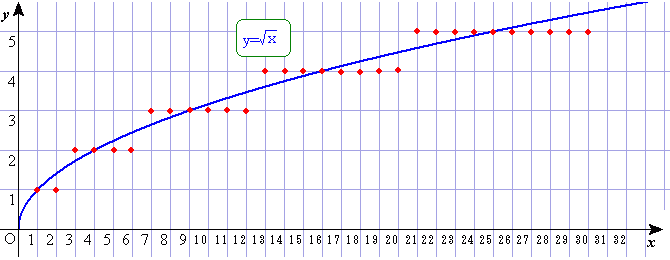
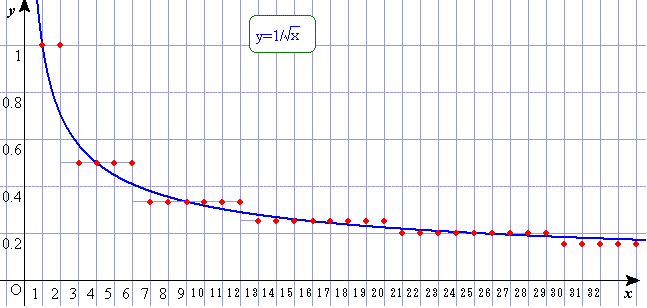
ただし、この問題は、ａ_ｎの逆数を足していきますから、 先ほどのｙの値の逆数の値を考え、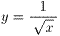のグラフ上に点を打ってみました。

この問題で求めている値は、ａ_ｎの逆数の和ですから、 下の図の塗りつぶした部分の面積になります。
階段状の１段ごとの面積が、ちょうと「２」になっています。

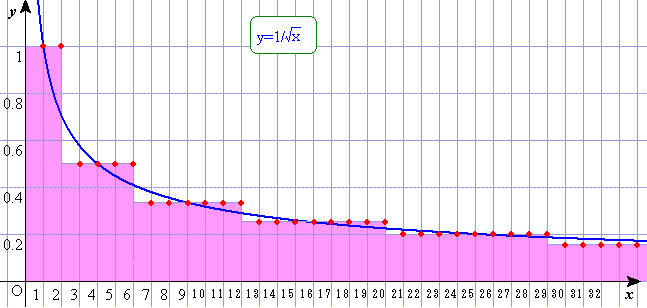
これは、関数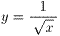の定積分の値にほぼ等しいのではないかと思いますよね？
試しに計算をしてみました。

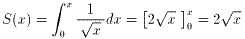
x=2008を代入してみます。

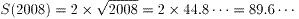
因みに、解答である　3988/45=88.2・・・です。

---