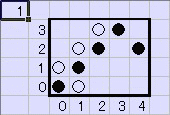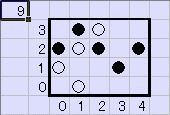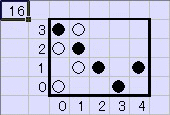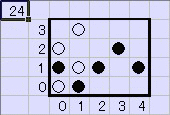
栤戣161丂僶僗偺塣峴
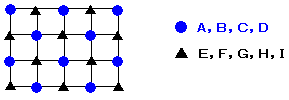
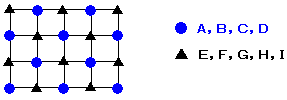
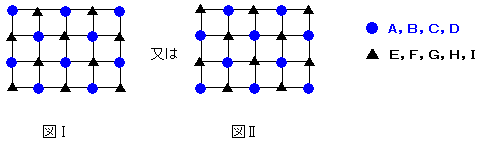
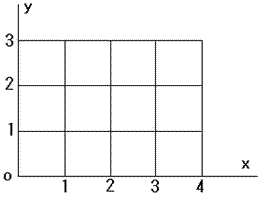
恾偵傛偆偵岄斦偺栚忬偺摴偑偁傝丄俀偮偺摴偑弌夛偆揰傪岎嵎揰偲屇傇偙偲偵偟傑偡丅
奺峴丄奺楍偵侾戜偢偮丄崌寁俋戜偺僶僗傪憱傜偣傑偡丅
偦傟偧傟偺僶僗偼摨偠懍偝偱憱傝丄侾偮偺峴傑偨偼楍傪墲暅偟偮偯偗傑偡丅
弶傔偼偳偺僶僗傕偄偢傟偐偺岎嵎揰偵抲偔傕偺偲偟傑偡丅
偳偺俀戜傕墲暅偺娫偵偳偙偐偺岎嵎揰偱弌夛偆偙偲偑側偄傛偆偵偡傞偙偲偑壜擻偱偟傚偆偐丅
晄壜擻偱偁傟偽徹柧偟丄壜擻偱偁傟偽偳偺傛偆側偲偒偐傪帵偟偰偔偩偝偄丅
丂丂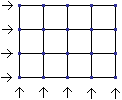
栤戣偺弌揟
僕儏僯傾悢妛僆儕儞僺僢僋2003-2008
悢妛僆儕儞僺僢僋嵿抍曇
擔杮昡榑幮
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗揮埵斀墳乯
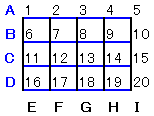
壓恾偺捠傝丄岎嵎揰偵1偐傜20偺斣崋傪晅偗丄
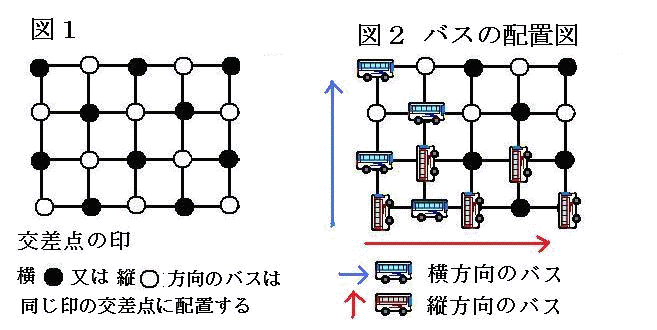
峴傪墲暅偡傞僶僗傪偦傟偧傟俙丄俛丄俠丄俢丄楍傪墲暅偡傞僶僗傪俤丄俥丄俧丄俫丄嘥偲偡傞丅
僶僗偼峴傑偨偼楍傪墲暅偟懕偗丄捠夁偡傞岎嵎揰偺悢偼峴傪侾墲暅偡傞偲俉丄楍傪侾墲暅偡傞偲俇側偺偱丄
偦傟傜偺嵟彫岞攞悢偱偁傞俀係偑侾僒僀僋儖偵捠夁偡傞岎嵎揰偺悢偱偁傞丅
奺僶僗偑捠夁偡傞岎嵎揰傪侾僒僀僋儖偵偮偄偰惍棟偡傞偲昞侾偺傛偆偵側傞偺偱丄偙傟傜偺働乕僗偐傜
慡偰偺僶僗偑岎嵎揰偱弌夛傢側偄傛偆側慻崌偣傪慖戰偡傟偽椙偄丅
愭偢丄俙傪岎嵎揰侾偐傜僗僞乕僩偝偣丄俤偑俙偲弌夛偆偙偲偑側偄傛偆偵俤偑僗僞乕僩偡傞岎嵎揰傪媮傔傞丅
昞侾偐傜丄俤偑岎嵎揰俇丄侾俇偐傜僗僞乕僩偡傞偲俙偲岎嵎揰侾偱弌夛偆偙偲偼側偄丅
偙偺応崌丄俤偑岎嵎揰俇偐傜僗僞乕僩偡傞曽岦偼丄岎嵎揰侾埥偄偼侾侾偺壗傟偺曽岦偱傕椙偄丅
摨條偵偟偰丄俛偑岎嵎揰俇偱俤偲弌夛傢側偄傛偆偵丄俛偑僗僞乕僩偡傞岎嵎揰傪媮傔傞丅
埲壓丄婛偵寛掕偟偨僶僗偺宱楬偵懳偟偰巆傝偺僶僗偑僗僞乕僩偡傞岎嵎揰傪弴師丄媮傔偰峴偗偽椙偄丅
昞侾
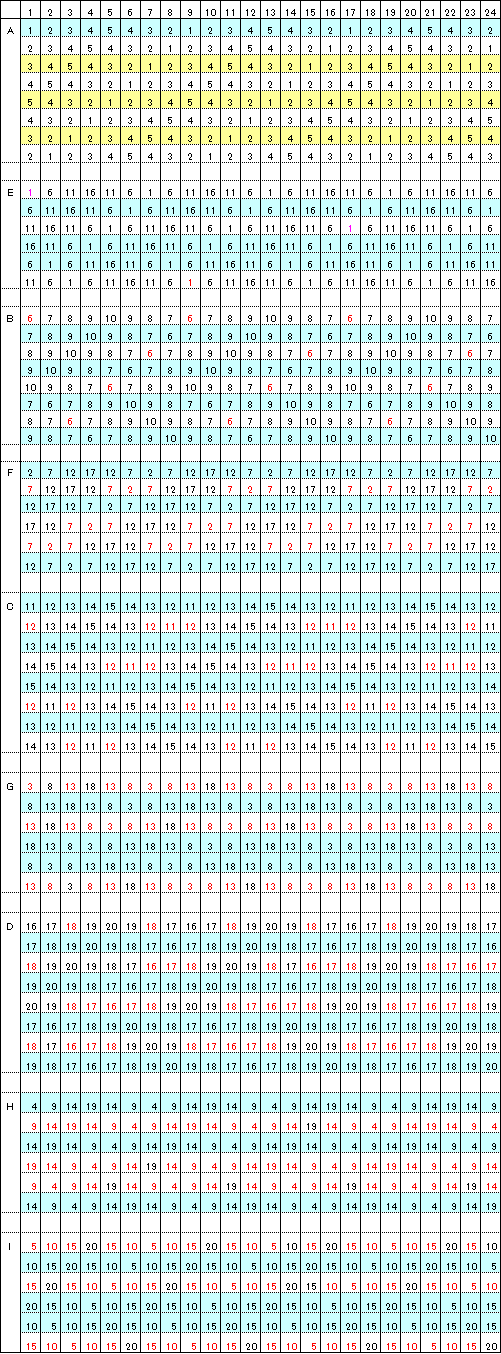
埲忋丄俙傪岎嵎揰侾偐傜僗僞乕僩偝偣丄慡偰偺僶僗偑岎嵎揰偱弌夛傢側偄傛偆偵丄懠偺僶僗偑僗僞乕僩偡傞
岎嵎揰偺埵抲傪媮傔傞偲壓恾偺捠傝偲側傞丅側偍丄僶僗偑岎嵎揰偐傜僗僞乕僩偡傞曽岦偑俀捠傝偁傞応崌偼丄
壗傟偐侾偮傪擟堄偵慖戰偱偒傞丅乮昞侾偺悈怓栐妡偗偺働乕僗乯
偙偙偱丄昞侾傛傝丄俙偑僗僞乕僩偡傞岎嵎揰偼丄侾偺懠偵俁丄傑偨偼俆偱傕椙偄偙偲偑暘偐傞偺偱丄捛婰偡傞偲
壓恾偺捠傝偲側傞丅乮昞侾偺墿怓栐妡偗偺働乕僗乯
傑偨丄俙偑僗僞乕僩偡傞岎嵎揰傪俀丄係偲偟偨応崌偼丄昞侾偺怓傪晅偗偰偄側偄働乕僗偑奩摉偡傞偺偱丄
忋恾偺仠偲仯傪擖傟懼偊傟偽椙偄丅
傛偭偰丄奺僶僗偑岎嵎揰偱弌夛偆偙偲側偔丄墲暅偡傞偙偲偼壜擻偱偁傞丅
嬶懱揑曽朄偼丄恾嘥丄傑偨偼恾嘦偺壗傟偐傪慖戰偟偰丄奺僶僗偑僗僞乕僩偡傞岎嵎揰傪侾偐強慖掕偡傞丅
扐偟丄岎嵎揰偐傜僗僞乕僩偡傞曽岦偑俀捠傝偁傞応崌偼丄壗傟偺曽岦偱傕椙偄丅
夝摎丒偦偺2
乮儁儞僱亅儉丗falcon@拞妛嫵巘乯
壜擻丅
僗僞乕僩帪偺攝抲偼條乆偩偑丄堦椺偼壓恾偺捠傝丅乮栴報偼僶僗偺恑峴曽岦傪昞偟偰偄傞丅乯
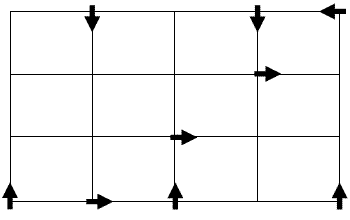
亙峫偊曽亜
忋壓偵摦偔僶僗偼6夞偺堏摦偱尦偺埵抲偵栠傞丅
嵍塃偵摦偔僶僗偼8夞偺堏摦偱尦偺埵抲偵栠傞丅
偟偨偑偭偰偙偺9戜偺僶僗偺埵抲偼俇偲俉偺嵟彫岞攞悢偱偁傞24夞偺堏摦偱尦偵栠傞丅
忋婰偺偙偲傪傕偲偵偟側偑傜丄嵟傕嵍偱忋壓偵摦偔僶僗偺弶婜埵抲傪屌掕偟丄
嵍塃偵摦偔僶僗偺弶婜埵抲傪丄屌掕偟偨僶僗偲24夞偺堏摦偺拞偱岎嵎揰偱弌夛傢側偄傛偆偵挷傋傞偙偲偵偟偨丅
偦偺寢壥偁傞掱搙偺巜恓偑棫偭偨偺偱丄帋偟偵愝掕偟偨弶婜埵抲偐傜24夞偺堏摦傪幚嵺偵峴偄丄
壜擻偱偁傞偙偲偑敾柧偟偨丅
夝摎丒偦偺3
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
廳側傞偲偒擇偮偺嵗昗偺榓偼昁偢嬼悢偵側傞偺偱...
偦偆側傜側偄傛偆側弶婜抣偵攝抲偡傟偽傛偄丅
嵍壓傪(0,0) 偲偡傞嵗昗偱峫偊傞偲...
墶偵摦偔僶僗丂丂廲偵摦偔僶僗
(嬼悢丄嬼悢(0))-(嬼悢(0)丄婏悢)
(婏悢丄婏悢(1))-(婏悢(1)丄嬼悢)
(嬼悢丄嬼悢(2))-(嬼悢(2)丄婏悢)
(婏悢丄婏悢(3))-(婏悢(3)丄嬼悢)
丂丂丂丂丂 丂 -(嬼悢(4)丄婏悢)
偨偲偊偽...
(0,0)-(0,1)
(1,1)-(1,2)
(2,2)-(2,3)
(3,3)-(3,0)
-(4,1)
偱傕偄偄偼偢...?
夝摎丒偦偺4
乮儁儞僱亅儉丗僆儎僕乯
奺岎嵎揰偱弌夛偆偙偲偑柍偄條偵偡傞偙偲偑壜擻
佹丂挿曽宍偺奿巕偺嵍壓偺岎嵎揰傪尨揰乮侽丆侽乯偲偟丄
塃懁傪丄倃幉曽岦丆忋懁傪倄幉曽岦偲偟奺岎嵎揰偵丄乮捈岎乯嵗昗傪擖傟傞丅
奺岎嵎揰俹乮a丆b乯 乮丂a 亖侽丆侾丆俀丆俁丆係丂丂b 亖侽丆侾丆俀丆俁乯
偵懳偟偰丆壓婰偺條偵怓偯偗傪偡傞丅
丂丂俠乷俹乮a丆b乯乸亖丂愒丂乮丂扐偟丂a亄b丂亖丂嬼悢乯
丂丂俠乷俹乮a丆b乯乸亖丂敀丂乮丂扐偟丂a亄b丂亖丂婏悢乯
偙偙偱丄墶曽岦偵憱傞僶僗傪椺偊偽 敀怓偺岎嵎揰偐傜弌敪偝偣傞丅
摨條偵丂廲曽岦偵憱傞僶僗傪椺偊偽 愒怓偺岎嵎揰偐傜摨帪偵弌敪偝偣傞偲丄
丂丂墶丗敀仺愒仺敀仺愒仺丒丒丒仺敀仺愒仺丒丒丒
丂丂廲丗愒仺敀仺愒仺敀仺丒丒丒仺愒仺敀仺丒丒丒丂丂偲側傝
偳偺俀戜偺僶僗傕奺岎嵎揰偱弌夛偆偙偲偑柍偄丅
夝摎丒偦偺5
乮儁儞僱亅儉丗岼偺柌乯
摴楬偺岎嵎揰傪奿巕揰偲尒偰丄偦偺嵗昗傪埲壓偺條偵峫偊傞丅
偙偺條偵昞偣偽慡偰偺岎嵎揰偼嵗昗偱昞偣丄倶偲倷嵗昗偺崌寁偼昁偢嬼悢偐婏悢偲側傞丅場偭偰丄墶4杮偺摴楬奺乆偵抲偔4戜偺僶僗慡偰傪崌寁嵗昗嬼悢偵抲偄偨応崌偼丄廲5杮偺摴楬奺乆偵抲偔5戜偺僶僗偺嵗昗傪慡偰崌寁嵗昗婏悢売強偵妱傝怳傟偽丄岎嵎揰偱2戜偑傇偮偐傞帠偼側偄丅
栜榑丄廲偲墶偺嵗昗崌寁傪媡偵偟偰傕椙偄丅扐偟丄廲偺5戜偼慡偰婏悢側傜婏悢丄嬼悢側傜嬼悢偲偣偹偽側傜側偄丅
夝摎丒偦偺6
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊偼壜擻偱偡丅
岎嵎揰傪仜偲仠偱恾偺傛偆偵報傪偮偗傑偡丅
廲偺僶僗偼仜偵攝抲偡傞丅墶偺僶僗偼仠偵攝抲偡傞丅
攝抲偡傞応強偼楍忋偵堦戜偱偁傟偽壗張偵攝抲偟偰傕椙偄偺偱偡丅
憱傞曽岦偼廲偺僶僗偼忋曽岦偱傕壓曽岦偱傕椙偄偺偱偡丅
墶曽岦偼塃曽岦偱傕嵍曽岦偱傕椙偄偺偱偡丅
棟桼偼廲曽岦偺僶僗偼憱傝偩偡偲敀仺崟仺敀仺崟偺弴偵捠夁偟傑偡丅
墶偺曽岦偼崟仺敀仺崟仺敀偺弴斣偵捠夁偟傑偡丅廬偭偰摨偠帪娫偵偼廲偺僶僗偲摨偠報偺岎嵎揰偼捠夁偟傑偣傫丅
廲偑仠偱偁傟偽墶偑仜丄廲偑仜偱偁傟偽墶偑仠偵攝抲偟傑偡丅廬偭偰攝抲応強偺慻崌偣偼懡偔偁傝傑偡丅
夝摎丒偦偺7
乮儁儞僱亅儉丗haya乯
偳偙偐偺岎嵎揰偱弌夛偆偙偲偑側偄傛偆偵偡傞偙偲偼壜擻偱偡丅丂
椺偊偽丄暘偐傝傗偡偔偡傞偨傔偵丄楍傪忋壓偡傞僶僗傪仠丄峴傪嵍塃偵摦偔僶僗傪仜偱昞偡偲偟偰丄
偺傛偆偵丅
亂夝偒曽亃
楍傪忋壓偡傞僶僗偼6夞栚偵丄峴傪嵍塃偵峴偒棃偡傞僶僗偼8夞栚偵摨偠応強偵栠傝傑偡偐傜丄
嵟彫岞攞悢偼24偱丄25夞栚偵偼摨偠嬊柺偵栠傝傑偡丅
堦斣嵍偺楍偲堦斣壓偺峴傪峴偒棃偡傞僶僗偵尷掕偟偰丄尨揰偱弌夛偭偨忬嫷偐傜摦偐偟巒傔偰丄
丂丂0,0 乮仸嵍偺悢抣偑仠偺丄塃偑仜偺尨揰偐傜偺嫍棧傪昞偟傑偡乯
丂丂1,1
丂丂2,2
丂丂3,3
丂丂2,4
丂丂1,3
丂丂0,2
丂丂2,0
丂丂3,1
丂丂0,4
偺搒崌9庬椶偑巊梡晄壜偺慻崌偣偩偲暘偐傝傑偡丅丂偙偙偱偺仠偲仜偺慻崌偣偺悢偼丄
丂丂丂3+4*4=19
偱偡偐傜丄巆傝偺巊偊傞慻崌偣偼10庬椶偱偡丅丂壖偵丄巊梡壜偺 0,1 偐傜巒傔傞偲偟偰丄
丂丂0,1
丂丂1,2
丂丂2,3
丂丂3,4
丂丂丒丒丒
丂丂1,0
丂丂2,1
丂丂3,2
丂丂丒丒丒
丂丂1,4
丂丂0,3
丂丂丒丒丒
丂丂3,0
丂丂丒丒丒
偲尵偆嬶崌偵幚嵺偵巆傝偺10庬椶偱徴撍偣偢偵塣峴壜擻偱偟偨丅
摨偠庤朄偱慻崌偣傪揔摉偵埪暘偟偨傕偺偑恾偺椺側偺偱偡偑丄幚嵺偵徴撍偣偢偵塣峴偱偒傑偡丅
夝摎丒偦偺8
乮儁儞僱亅儉丗俼倄倀1128乯
師偺傛偆側恾傪峫偊傑偡丅堦偮偺岎嵎揰偐傜師偺岎嵎揰傑偱偺摓払帪娫偼丄侾扨埵帪
娫偲偟傑偡丅敀娵偼弌敪乮帪崗侽)偐嬼扨埵帪崗偱偡丅崟娵偼婏扨埵帪崗偱偡丅
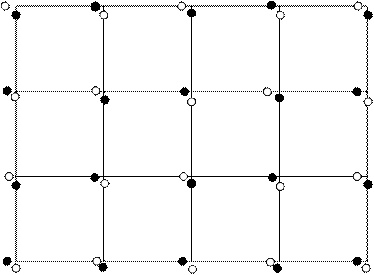
墶幉忋偺娵偼墶偺墲暅丄廲幉忋偺娵偼廲偺墲暅偱偡丅
嬼帪崗偲婏帪崗偼弌夛偄傑偣傫偺偱恾偵廬偭偰敀娵傪奺弌敪揰偲偡傟偽傛偄偙偲偵側
傝傑偡丅
崟娵偲敀娵傪擖傟懼偊偰傕惉傝棫偪傑偡丅
寁嶼偑柺搢側偺偱徣偒傑偡偑丄弌敪揰偺応崌偺悢偐傜丄慡偰偺慻傒崌傢偣偑壗捠傝偵
側傞偐傕寁嶼偱偒偦偆偱偡偹両
偝傜偵曗懌偱偡偑丄嵍壓傪寛傔傞偲僪儈僲幃偵屻偺偡傋偰偑寛傑偭偰偟傑偆偺偱丄
敀崟偺慻傒崌傢偣偼丄恾偲恾偺敀崟傪擖傟懼偊偨働乕僗偟偐偁傝傑偣傫丅
傑偨擟堄偺岎嵎揰偱廲墶偄偢傟傕敀娵乮嬾帪崗乯傑偨偼偄偢傟傕崟娵乮婏帪崗乯偺応
崌丄奺乆偺墲暅夞悢傪揔摉偵偊傜傇偙偲偵傛傝廃婜揑偵昁偢堦抳偡傞偺偼帺柧偱偡丅
夝摎丒偦偺9
乮儁儞僱亅儉丗偺偭偙傫乯
奺岎嵎揰偵敀愇偲崟愇傪岎屳偵抲偔
丂丂仜仠仜仠仜 丂丂仠仜仠仜仠 丂丂仜仠仜仠仜 丂丂仠仜仠仜仠
楍傪憱傞僶僗傪俙丄峴傪憱傞僶僗傪俛偲偡傞
偡傋偰偺俙乮俆戜乯傪仜偺忋丄
偡傋偰偺俛乮係戜乯傪仠偺忋偵抲偔偙偲偑偱偒傟偽
偳偺俀戜傕岎嵎揰偱弌夛偆偙偲偼側偄
丂仸偡傋偰偺俙偑仠偺忋丄偡傋偰偺俛偑仜偺忋偱傕峔傢側偄
椺偊偽師偺傛偆偵抲偗偽傛偄偐傜丄弌夛傢側偄傛偆偵偡傞偙偲偼壜擻偱偁傞
乮侾乯丂俙俛亅亅俙丂丂丂乮俀乯丂丂亅亅亅俛俙丂丂丂乮俁乯丂亅亅俙俛亅 丂丂丂丂亅俙俛亅亅丂丂丂丂丂丂丂丂亅亅俛俙亅丂丂丂丂丂丂丂亅俙俛俙亅 丂丂丂丂亅亅俙俛亅丂丂丂丂丂丂丂丂俙俛俙亅亅丂丂丂丂丂丂丂俙俛亅亅俙丂丂丂丂 丂丂丂丂亅亅亅俙俛丂丂丂丂丂丂丂丂俛俙亅亅亅丂丂丂丂丂丂丂俛亅亅亅亅丂丂丒丒丒丒丒丒
夝摎丒偦偺10
乮儁儞僱亅儉丗柪巕偺梇擫乯
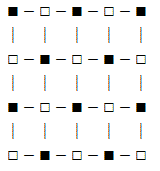
忋壓曽岦偵堏摦偡傞僶僗偼忋婰偺仩偺岎嵎揰偵
嵍塃曽岦偵堏摦偡傞僶僗偼忋婰偺仭偺岎嵎揰偵攝抲偡傞丅乮傑偨偼偦偺媡乯
忋壓曽岦偺僶僗偲嵍塃曽岦偺僶僗偑岎嵎揰偱弌夛偆偨傔偵偼丄
偁傞帪揰偱摨偠怓偺岎嵎揰偵嫃側偗傟偽偄偗側偄丅
弶婜攝抲偐傜偼丄忋壓曽岦偺僶僗偑仭偺岎嵎揰偵堏摦偡傞偲偒偵偼丄
嵍塃曽岦偺僶僗偼仩偺岎嵎揰偵堏摦偟偰偄傞偺偱丄
偳偺俀戜傕墲暅偺娫偵偳偙偐偺岎嵎揰偱弌夛偆偙偲偑側偄丅
夝摎丒偦偺11
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
岄斦偺栚忬偺摴傪恾偺傛偆偵嵗昗暯柺偺拞偵偍偔偙偲偵偟傑偡丅
僶僗偑侾嬫夋恑傓偺偵偐偐傞帪娫傪扨埵帪娫偲偟傑偡丅
倷幉忋偵偁傞僶僗偑偁傞峴傪嵍塃偵堏摦偡傞偲偒丄奺楍傪捠夁偡傞帪娫傪挷傋傑偡丅
昞侾
| (0,*) | (1,*) | (2,*) | (3,*) | (4,*) |
|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 |
| 8 | 7 | 6 | 5 | 丂 |
| 丂 | 9 | 10 | 11 | 12 |
| 16 | 15 | 14 | 13 | 丂 |
| 丂 | 17 | 18 | 丒丒丒 | 丒丒丒 |
倶幉忋偵偁傞僶僗偑偁傞楍傪忋壓偵堏摦偡傞偲偒奺峴傪捠夁偡傞帪娫傪挷傋傑偡丅
昞俀
| (*,3) | 3 | 丂 | 9 | 丂 | 15 | 丂 |
|---|---|---|---|---|---|---|
| (*,2) | 2 | 4 | 8 | 10 | 14 | 16 |
| (*,1) | 1 | 5 | 7 | 11 | 13 | 丒丒丒 |
| (*,0) | 0 | 6 | 丂 | 12 | 丂 | 丒丒丒 |
偙偙偱丄奺嵗昗揰偱僶僗偑弌夛偆偐偳偆偐傪挷傋傑偡丅
乽亅乿偼弌夛傢側偄偙偲丄乽亊乿偼弌夛偆偙偲傪昞偟傑偡丅
椺偊偽丄(2,1)偺抧揰偼丄
嵍塃偵堏摦偡傞僶僗偼丄帪娫乷2,6,10,14,ゥp偵捠夁偟傑偡丅乮昞侾偺搷怓乯
忋壓偵堏摦偡傞僶僗偼丄帪娫乷1,5,7,11,13,ゥp偵捠夁偟傑偡丅乮昞俀偺悈怓乯
偙傟傜偺帪娫傪傒傞偲丄嬼悢偲婏悢側偺偱摨偠帪娫偼側偔丄弌夛傢側偄偙偲偑暘偐傝傑偡丅
| 丂 | (0,*) | (1,*) | (2,*) | (3,*) | (4,*) |
|---|---|---|---|---|---|
| (*,3) | 亅 | 亊 | 亅 | 亊 | 亅 |
| (*,2) | 亊 | 亅 | 亊 | 亅 | 亊 |
| (*,1) | 亅 | 亊 | 亅 | 亊 | 亅 |
| (*,0) | 亊 | 亅 | 亊 | 亅 | 亊 |
偙偺寢壥偐傜丄師偺恾偺傛偆偵傑偢僶僗傪攝抲偟傑偡丅
娍帤偼丄偦偺怓偺僶僗偑捠夁偡傞帪娫偺嬼悢丄婏悢傪昞偟傑偡丅
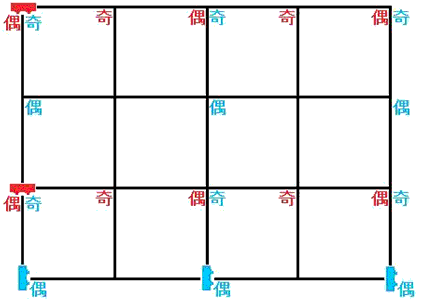
師偵巆傝偺僶僗傪捠夁帪娫偺嬼悢丄婏悢偵拲堄偟偰丄椺偊偽師偺傛偆偵攝抲偟傑偡丅
偡傞偲偳偺抧揰傕嬼悢丄婏悢偑摨偠偵側傜側偄偺偱偳偺俀戜偺僶僗傕弌夛偆偙偲偑偁傝傑偣傫丅
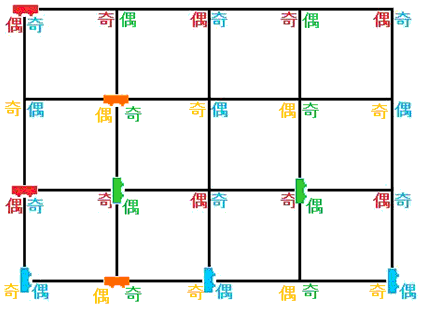
偮傑傝嬼悢丄婏悢偑廳側傜側偗傟偽傛偄偺偱丄
愒娵傪峴傪嵍塃偵堏摦偡傞僶僗偺攝抲偺岓曗抧丄惵巐妏傪楍傪忋壓偵堏摦偡傞僶僗偺攝抲偺岓曗抧偲偡傞偲丄
偙偺恾偱偼丄
丂丂丂乮俁亊俀亊俁亊俀乯亊乮俀亊俀亊俀亊俀亊俀乯
捠傝偺攝抲偑偁傝傑偡丅
傑偨丄愒娵偲惵巐妏傪擖傟懼偊偰傕傛偄偺偱偝傜偵攞偟偰丄
丂丂丂俀亊乮俁亊俀亊俁亊俀乯亊乮俀亊俀亊俀亊俀亊俀乯亖俀俁侽係
捠傝偺攝抲偑偁傝傑偡丅
夝摎丒偦偺12
乮儁儞僱亅儉丗T_Tatekawa乯
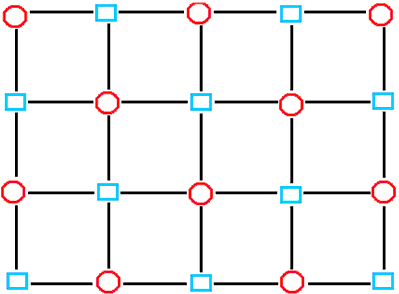
岎嵎揰傪巗徏柾條偵揾傝傑偡丏嵍壓傪崟丆偙偙偺岎嵎揰偺椬傪敀偲偄偆傛偆偵偟傑偡丏
丂丂丂仩仭仩仭仩 丂丂丂仭仩仭仩仭 丂丂丂仩仭仩仭仩 丂丂丂仭仩仭仩仭
師偵丆僶僗傪攝抲偟傑偡丏廲偵憱傞僶僗偼崟偺岎嵎揰丆墶偵憱傞僶僗偼敀偺
岎嵎揰偵攝抲偟傑偡丏偡傞偲丆僶僗偼岎嵎揰偱弌夛偄傑偣傫丏
帪娫偑宱偭偰堦僽儘僢僋恑傓偲丆廲偵憱傞僶僗偼敀偺岎嵎揰丆墶偵憱傞僶僗偼
崟偺岎嵎揰偵嫃傞偺偱丆廲偵憱傞僶僗偲墶偵憱傞僶僗偼岎嵎揰偱弌夛偄傑偣傫丏
傑偨帪娫偑宱偭偰堦僽儘僢僋恑傓偲丆廲偵憱傞僶僗偼崟偺岎嵎揰丆墶偵憱傞僶僗偼
敀偺岎嵎揰偵嫃傞偺偱丆廲偵憱傞僶僗偲墶偵憱傞僶僗偼岎嵎揰偱弌夛偄傑偣傫丏
偙偺孞傝曉偟偵傛傝丆僶僗偑岎嵎揰偱弌夛傢側偄傛偆偵偡傞帠偼壜擻偱偡丏
偮傑傝岎嵎揰傪巗徏柾條偵揾傝丆廲偵憱傞僶僗丆墶偵憱傞僶僗傪摨偠怓偺岎嵎揰偵攝抲偡傟偽壜擻偱偡丏
惓夝幰
| 栭傆偐偟偺偮傜偄偍偠偝傫 | 偺偭偙傫 | 柪巕偺梇擫 |
| 岼偺柌 | 僗儌乕僋儅儞 | 忨偺偍偠偝傫 |
| haya | 俼倄倀1128 | 揮埵斀墳 |
| falcon@拞妛嫵巘 | 僆儎僕 | T_Tatekawa |
僐儊儞僩
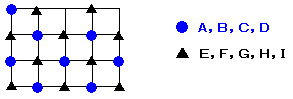
壜擻偱偡偹丅奆偝傫偺夝摎偵偁傞傛偆偵丄岎嵎揰傪敀崟偺巗徏柾條偵揾傝暘偗丄 椺偊偽廲曽岦偺僶僗偼崟岎嵎揰偐傜丄墶曽岦偺僶僗偼敀岎嵎揰偐傜弌敪偝偣傟偽丄 屳偄偵傇偮偐傞偙偲偼側偄偲偄偆偙偲偑傢偐傝傑偡丅 僷儕僥傿乮嬼婏惈乯偱峫偊傞儅僗栚偺栤戣偺椶帡栤戣偱偡偹丅
 top
top