侾俁侾丏儅僗栚偺栤戣
栤戣侾
壓塃恾偺儅僗栚傪丄壓嵍恾偺侾亊俀偺挿曽宍偱晘偒偮傔傞偙偲偑偱偒側偄偙偲傪帵偣丅
偨偩偟丄挿曽宍偼夞揮偝偣偰巊偭偰傕傛偄偑丄屳偄偵廳側偭偨傝丄儅僗栚偐傜
偼傒弌偟偨傝偟偰偼偄偗側偄傕偺偲偡傞丅
丂丂丂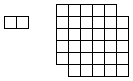
栤戣俀
侾侽亊侾侽偺儅僗栚傪壓偺俿帤宆偺恾宍俽偱晘偒偮傔傞偙偲偑偱偒側偄偙偲傪帵偣丅
偨偩偟丄恾宍俽偼夞揮偝偣偰巊偭偰傕傛偄偑丄屳偄偵廳側偭偨傝丄惓曽宍偐傜偼傒弌偟偨傝
偟偰偼偄偗側偄傕偺偲偡傞丅
丂丂丂
栤戣偺弌揟
僕儏僯傾悢妛僆儕儞僺僢僋
悢妛僆儕儞僺僢僋嵿抍曇
婽彂朳敪峴
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗僗儌乕僋儅儞乯
栤戣1
巗徏柾條偵傢偗傞偲丄崟敀摨悢偱側偄偲柍棟偱偡偑丄梌偊傜傟偨恾偼丄婏悢偺偨傔柍
棟丅
夝摎丒偦偺2
乮儁儞僱亅儉丗俽俷倀乯
栤戣侾
儅僗栚偵怓傪敀崟偺怓傪偮偗丄

偲偡傞丅仩偑侾俇屄丄仭偑侾俉屄偲側傞丅
侾倶俀偺恾宍偱杽傔傞偙偲傪峫偊傞偲丄昁偢仩偲仭偑堦屄偢偮尭偭偰偄偔偙偲偵側傞偑丄
嵟廔揑偵昁偢仭偑俀偮偁傑傞偙偲偵側傝丄屳偄偵椬愙偟偰偄側偄俀儅僗偑巆傞偙偲偵側傞丅
偟偨偑偭偰丄晄壜擻偲偄偊傑偡丅
夝摎丒偦偺3
乮儁儞僱亅儉丗僆儎僕乯
乮侾乯
峴楍偺條偵惉暘偵暘偗偰峫偊傞
暘偐傝傗偡偄條偵師偺條偵怓暘偗偡傞丅椺偊偽 倝峴倞楍傪
丂丂丂俙倝倞丂亖倝亄倞亖丂嬼悢丗敀
丂丂丂俙倝倞丂亖倝亄倞亖丂婏悢丗崟
偲偡傞丅侾亊俀丂偼丄敀侾屄偲崟侾屄偲側傞丅 恾偺丂俁係屄丂偺怓暘偗傪峫偊傞偲
丂丂丂丂俇亊俇亅俙侾俇亅俙俇侾丂
丂丂丂亖乮敀侾俉屄丂偲丂崟侾俉屄乯亅崟俀屄
丂丂丂亖乮敀侾俉屄乯偲乮崟侾俇屄乯丂
偲側傝乮敀崟摨悢偑丂侾亊俀丂偱晘偒偮傔傜傟傞昁梫忦審偱偁傞偑乯
敀偺怓偲崟偺怓偑摨悢偱側偄偨傔偵丄侾亊俀亖敀侾屄偲崟侾屄丂偺帺慠悢攞偲側傜偢丄
侾亊俀丂偱晘偒偮傔傜傟側偄丅
乮俀乯
乮侾乯偲摨條偵峫偊丂侾侽亊侾侽偼丄敀俆侽屄丂偲丂崟俆侽屄丂偺摨悢偲側傜側偗傟偽側傜側偄丅
係屄偺俿帤宆偱偼丄怓暘偗偼俀庬椶峫偊傜傟傞丅
丂丂丂嘥庬栚偼丄敀侾屄偲崟俁屄偺俿帤宆
丂丂丂嘦庬栚偼丄敀俁屄偲崟侾屄偺俿帤宆
偑峫偊傜傟傞丅俿帤宆偱晘偒偮傔傞堊偵偼丄嘥庬栚偲嘦庬栚偑摨悢偲側傞帠偑昁梫忦審丄
傛偭偰嘥庬栚偲嘦庬栚偑懳偺丂俉屄偺帺慠悢攞偲側傞帠偑昁梫偩偑丄
丂丂丂侾侽亊侾侽亐俉亖侾俀丏俆
偲側傝丄帺慠悢攞偲側傜側偄丅
傛偭偰丄俿帤宆偱晘偒偮傔傜傟側偄丅
夝摎丒偦偺4
乮儁儞僱亅儉丗偺偭偙傫乯
栤戣侾
偙偺侾俈忯偺晹壆傪忯偱晘偒偮傔傞偙偲偑偱偒側偄偙偲傪帵偣偽傛偄
忯偼俀儅僗暘偺挿曽宍偩偐傜
晹壆傪巗徏柾條偵揾傝暘偗傞偲
侾偮偺忯偼昁偢敀侾儅僗偲崟侾儅僗偺慻傪愯傔傞
傛偭偰揾傝暘偗偨帪丄敀儅僗偲崟儅僗偺悢偼摨偠偱側偗傟偽側傜側偄
偲偙傠偑偙偺俁係嬫夋傪巗徏柾條偵揾傝暘偗傞偲
敀侾俉儅僗崟侾俇儅僗乮偁傞偄偼偦偺媡乯偲側傞
敀儅僗偲崟儅僗偺悢偑堎側傞偐傜丄晘偒偮傔傞偙偲偼偱偒側偄
栤戣俀
偙偺俀俆忯偺晹壆傪S偺宍傪偟偨忯偱晘偒偮傔傞偙偲偑偱偒側偄偙偲傪帵偣偽傛偄
侾侽侽嬫夋傪巗徏柾條偵揾傝暘偗傞偲敀俆侽儅僗崟俆侽儅僗偲側傞
S偺宍傪偟偨忯偼昁偢敀俁儅僗崟侾儅僗丄偁傞偄偼敀侾儅僗崟俁儅僗偺慻傪愯傔傞
傛偭偰敀俁儅僗崟侾儅僗偺慻傪愯傔傞忯偺悢傪x 偲偡傞偲
丂敀儅僗偼慡晹偱丂3x+(25-x)=25+2x
丂崟儅僗偼慡晹偱丂3(25-x)+x=75-2x 偲側傞
椉曽偲傕婏悢偲側傝丄
敀俆侽儅僗崟俆侽儅僗偲側傞偙偲偼側偄偐傜丄晘偒偮傔傞偙偲偼偱偒側偄
夝摎丒偦偺5
乮儁儞僱亅儉丗teki乯
侾丂敀崟偺巗徏柾條偵揾傝暘偗傟偽偡偖偵傢偐傝傑偡偑丄恾偺恾宍偼敀偲崟偺屄悢偑堘偆
乮僷儕僥傿偑堘偆乯偺偱丄敀崟侾屄偢偮偺恾宍偱杽傔崬傓偙偲偑偱偒傑偣傫丅
俀丂偪傚偭偲暋嶨偱偡偑丄侾侽亊侾侽偺惓曽宍偼丄係亊俀俆屄偺梌偊傜傟偨恾宍偱杽傔傞
昁梫偑偁傝傑偡丅偲偙傠偑丄侾侽亊侾侽偺惓曽宍偼侾偲摨條偵敀崟偺巗徏柾條偵揾傝暘偗傞偲丄
敀俆侽屄丄崟俆侽屄偵揾傝暘偗傜傟傞偺偱丄梌偊傜傟偨恾宍乮敀崟偺嵎偑亇俀乯偱揾傝傢偗傞偵
偼偳偆偟偰傕嬼悢屄偺恾宍偑昁梫偲側傝傑偡丅傛偭偰丄杽傔崬傒偼晄壜擻偱偡丅
夝摎丒偦偺6
乮儁儞僱亅儉丗怣嶰乯
偳偪傜偺栤戣傕崟偲敀偺儅僗傪僠僃僢僇乕柾條偵慻傒崌傢偣偨僠僃僗斦
傪儀乕僗偵偟偰峫偊傑偡丅僠僃僗斦偑庤嫋偵側偄偺偱暘偐傝傑偣傫偑丄
嵍忋嬿傪敀偲偟傑偡丅
栤戣侾
俀屄偺儅僗偑宷偑偭偰弌棃偰偄傞栤戣偺扨埵曅偼丄偳偙偵丄偳偺岦偒偵抲偄偰傕
敀偲崟偺儅僗傪侾屄偢偮愯傔傑偡丅
栤戣偺椞堟偼俇X俇儅僗偺惓曽宍偐傜丄塃忋嬿偲丆嵍壓嬿偺丄俀屄偺儅僗傪
庢傝彍偄偨傕偺偱丆嵍忋嬿傪敀儅僗偲偡傟偽丄庢傝彍偐傟偨傕偺偼偳偪傜傕崟偱丄
椞堟偺憤寁偱丄敀儅僗侾俉屄丄崟儅僗侾俇屄偲側傝丄屄悢偑堎側傞偺偱丄
偙偺扨埵曅偩偗傪慻傒崌傢偣偰杽傔傞偙偲偑弌棃傑偣傫丅
栤戣俀
偙偺栤戣偺扨埵曅偼丄僠僃僗斦偺丄偳偙傊偳偺岦偒偵抲偄偰傕丄
敀儅僗俁屄偲崟儅僗侾屄偐丄媡偵丆崟儅僗俁屄偲敀儅僗侾屄傪愯傔傑偡丅
敀俁崟侾偺扨埵曅乽x乿屄偲丄崟俁敀侾偺扨埵曅乽y乿屄偱丄
椞堟傪杽傔傞偙偲偑弌棃傞偲偡傟偽丄椞堟偵偼敀崟摨悢偺俆侽屄偢偮偁傞偺偱丄
俁x亄y亖俆侽丄x亄俁y亖俆侽丂偱丄偙傟傜傪堷偒嶼偟偰丄x亖y偲側傝傑偡丅
偦偙偱丄係x亖係y亖俆侽丂偲側傝丄惍悢偺屄悢偱偙傟傪枮偨偡偙偲偼偱偒傑偣傫丅
夝摎丒偦偺7
乮儁儞僱亅儉丗Toru乯
栤戣侾
乮壓塃恾乯偺儅僗栚傪丄椺偊偽嵍忋傪敀偲偟偰丄敀偲敀丄崟偲崟偑椬傝崌傢側偄傛
偆偵丄敀崟偺巗徏柾條偵揾傞丅塃忋丄嵍壓偺妏偼杮棃丄崟偺偲偙傠偵側傞偺偱丄敀偺
傎偆偑2偮懡偔側傞丅侾x俀偺挿曽宍偼敀偑侾偮丄崟偑侾偮側偺偱丄偙傟傪側傜傋偰傕
敀崟偺悢偼摨偠偼偢偱丄晘偒偮傔傞偙偲偼偱偒側偄丅
栤戣俀
摨條偵峫偊傞偲丄恾宍S偼乮敀俁崟侾乯偁傞偄偼乮敀侾崟俁乯偱偁傞偑丄侾侽x侾侽
偺儅僗栚偼敀俆侽崟俆侽偱偁傞偐傜丄偙傟傜偼摨悢偱側偗傟偽側傜側偄丅偟偨偑偭偰
乮敀俁崟侾乯偲乮敀侾崟俁乯傪儁傾偵偟偰峫偊傞偲丄儅僗栚偺悢偼俉偺攞悢偱偁傞偙
偲偑昁梫偱丄侾侽x侾侽亖侾侽侽偼俉偺攞悢偱側偄偺偱偺晘偒偮傔傞偙偲偼偱偒側偄丅
夝摎丒偦偺8
乮儁儞僱亅儉丗俶偲乣乯
侾斣偼桳柤偱偡偹丅僠僃僗斦偺傛偆偵俇亊俇乕俀偺傑偡傪敀崟巗徏柾條
偵揾傝暘偗傞偲丄敀偺傑偡偲崟偺傑偡偺悢偑懙傢側偄偗傟偳丄抲偄偰偄偔
乮僪儈僲偺僐儅偺傛偆側乯挿曽宍偼堦曽偺惓曽宍偑崟傪杽傔丄懠曽偑敀傪
杽傔偰偄偔偺偱丄杽傔恠偔偡偵偼斦偺敀傑偡偲崟傑偡偺悢偑摨偠偱側偔偰
偼側傜側偄偐傜杽傔恠偔偣側偄丅
俀斣傕摨條偵侾侽亊侾侽偺傑偡傪敀崟巗徏柾條偵偡傞偲丄敀傑偡傕崟傑
偡傕俆侽偵側傞丅偲偙傠偑丄俿宆偺傕偺偼敀俁崟侾偐敀侾崟俁丅偙偺俿宆
偺傕偺偼惓曽宍偑係偮偁傞偺偱丄斦傪偪傚偆偳杽傔恠偔偣傞偲偟偨傜俿宆
偺恾宍俽傪俀俆屄巊偆偙偲偵側傞丅俽俀俆屄傪敀俁崟侾偲敀侾崟俁偵壗屄
偢偮妱傝怳傠偆偲傕丄晄岾側偙偲偵俀俆偼婏悢側偺偱敀崟摨悢偵偼偱偒側
偄丅傛偭偰丄偪傚偆偳杽傔恠偔偡偙偲偼偱偒側偄丅
偍傑偗丅栤戣恾傪尒傞偲丄俿宆偲偄偆傛傝偼丄撌宆偲偄偭偨曽偑偟偭偔
傝偔傞傛偆側乧乧丅
夝摎丒偦偺9
乮儁儞僱亅儉丗柪巕偺梇擫乯
栤戣侾
恾宍傪壓婰偺傛偆偵巗徏柾條偵揾傝暘偗傞丅崟儅僗偑俀屄懡偔側傞丅
侾亊俀偺挿曽宍傪偳偺傛偆偵抲偄偰傕丄崟敀侾偮偯偮偺儅僗傪愯傔傞偺偱丄
嵟屻偵偼崟儅僗偑俀屄梋傞丅崟儅僗摨巑偼椬愙偟偰偄側偄偺偱丄侾亊俀偺挿曽宍偱暍偆
偙偲偼晄壜擻丅

栤戣俀
栤戣侾偲摨條偵丄侾侽倃侾侽偺儅僗栚傪巗徏柾條偵揾傝暘偗傞偲丄崟儅僗偑俆侽屄丄敀
儅僗偑俆侽屄偵側傞丅
傕偟丄侾侽亊侾侽偺儅僗栚傪俿帤宆偺恾宍俽偱晘偒偮傔傞偙偲偑偱偒偨偲壖掕偡傞偲丄
恾宍俽偼俀俆屄巊梡偡傞偙偲偵側傞丅
俿帤宆偺恾宍俽傪偳偺傛偆偵抲偄偰傕丄崟侾偮偲敀俁偮傑偨偼崟俁偮偲敀侾偮偺儅僗傪
愯傔傞丅
恾宍俽偵昁偢娷傑傟傞崟侾偮偲敀侾偮偺儅僗傪彍偔偲丄俀俆屄偺崟儅僗偲敀儅僗偑巆傞
丅
巆傝偺儅僗栚偐傜丄恾宍俽侾偮偵晅偒丄崟儅僗俀偮傑偨偼敀儅僗俀偮傪庢傝彍偐傟傞偑
丄
俀屄偯偮庢傝彍偄偰丄俀俆屄偺崟儅僗傪庢傝彍偔偙偲偼偱偒側偄丅
傛偭偰丄恾宍俽偱晘偒偮傔傞偙偲偑偱偒偨偲偄偆壖掕偑岆偭偰偄傞偺偱丄
侾侽亊侾侽偺儅僗栚傪俿帤宆偺恾宍俽偱晘偒偮傔傞偙偲偑偱偒側偄丅
夝摎丒偦偺10
乮儁儞僱亅儉丗揮埵斀墳乯
栤戣侾丏
梌偊傜傟偨儅僗栚傪壓恾偺傛偆偵巗徏柾條偲偟偰怓暘偗偡傞丅
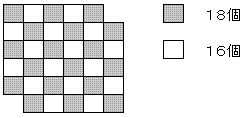
偝偰丄梌偊傜傟偨挿曽宍偵傕摨條偵怓傪晅偗丄偙偺挿曽宍偱晘偒媗傔傞偙偲偑偱偒傞偲壖掕偡傞偲丄
儅僗栚偺柺愊偐傜寁嶼偟偰侾俈屄偺挿曽宍偑昁梫偲側傝丄
挿曽宍傪峔惉偡傞惓曽宍偺悢傕丄偦傟偧傟侾俈屄偲側傞丅
偟偐偟丄偙傟傜偺惓曽宍偺悢偱偼丄忋婰偺巗徏柾條偵怓暘偗偱偒側偄丅
傛偭偰丄梌偊傜傟偨挿曽宍偱丄忋婰儅僗栚傪晘偒媗傔傞偙偲偼偱偒側偄丅
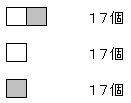
栤戣俀丏
摨條偵丄侾侽亊侾侽偺儅僗栚傪壓恾偺傛偆偵巗徏柾條偲偟偰怓暘偗偡傞丅

偝偰丄梌偊傜傟偨恾宍俽偵壓婰偺擇捠傝偺怓傪晅偗丄儅僗栚傪晘偒媗傔傞帠
偑偱偒傞偲壖掕偡傞偲丄儅僗栚偺柺愊偐傜寁嶼偟偰俀俆屄偺恾宍俽偑昁梫偲
側傞偑丄俀俆偼婏悢側偺偱丄峔惉偡傞偦傟偧傟偺惓曽宍偺悢傪俆侽屄偵偡傞偙偲偼偱偒側偄丅
椺偊偽丄

夝摎丒偦偺11
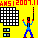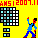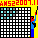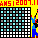 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
栤戣侾丏摎偊
晘偒媗傔傞帠偼弌棃傑偣傫丅
儅僗栚偺曅曽偵仠懠曽偵仜儅乕僋傪偮偗偰暲傋傞偲曅曽偑俀偮懡偔側偭偰偄傑偡丅
廬偭偰晘偒偮傔傞偙偲偼弌棃傑偣傫丅壓恾傪嶲徠
栤戣俀丏摎偊
侾侽亊侾侽偺儅僗栚傪T帤宆偱晘偒媗傔傞帠偼弌棃傑偣傫丅
晘偒偮傔傞儅僗栚偺俿帤宆偵恾偺傛偆偵崟丄敀儅乕僋傪偮偗偰傒傑偡丅
侾侽亊侾侽偺儅僗傔偵崟丄敀偺儅乕僋傪偮偗偰傒傑偡偲崟俆侽偱敀俆侽偱摨悢偵側傝傑偡丅
崟偲敀傪摨悢偵偡傞偵偼T帤宆傪嬼悢屄巊梡偟側偗傟偽側傝傑偣傫丅
丂丂丂侾侽侽亐係亖俀俆
偱嬼悢偱偼偁傝傑偣傫丅廬偭偰晘偒偮傔傞偙偲偼弌棃傑偣傫丅壓恾傪嶲徠
夝摎丒偦偺12
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
侾乯偼夝偒曽傪抦偭偰偄傑偟偨丅俀乯偼偦偺墳梡偱峫偊傑偟偨丅
摎偊侾乯壓偵傛偆偵巗徏柾條偵揾傝暘偗傞丅
侾亊俀偼昁偢敀崟偺僺乕僗偲側傞偑丄
偙偺柾條偼崟侾俉丄敀侾俇側偺偱偼傔崬傒偼晄壜擻丅

摎偊俀乯
摨條偵敀崟偺巗徏柾條偵揾傝暘偗傞丅
僺乕僗偼師偺偄偢傟偐丅

敀俆侽丄崟俆侽偁傞偺偱偙偺俀屄偺僺乕僗偼摨悢昁梫丅
偲偙傠偑丄慡僺乕僗偼俀俆屄偲婏悢側偺偱摨悢偵偼側傟側偄丅
乮偡側傢偪丄崟俆侽丄敀俆侽傪嶌傞偙偲偑偱偒側偄乯
屘偵偼傔偙傒偼晄壜擻丅
夝摎丒偦偺13
乮儁儞僱亅儉丗嶰妏掕婯乯
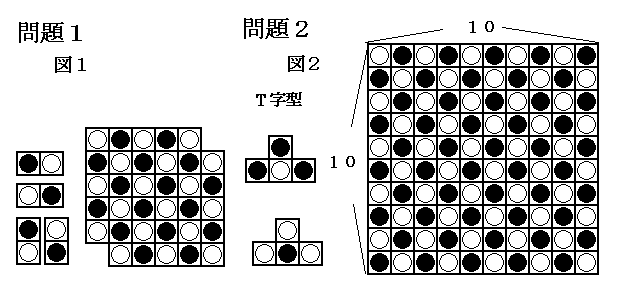
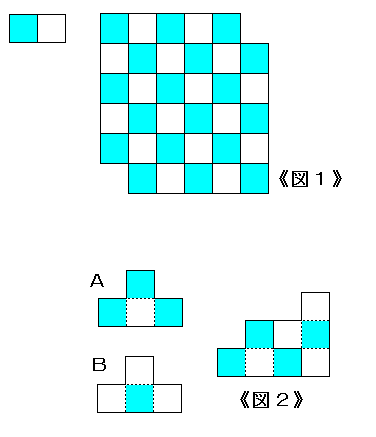 侾丏乻恾侾乼偺傛偆偵僪儈僲傪晘偒媗傔傞椞堟傪巗徏柾條偵揾傝暘偗傞偲丆
惵偑侾俉丆敀偑侾俇丅
侾丏乻恾侾乼偺傛偆偵僪儈僲傪晘偒媗傔傞椞堟傪巗徏柾條偵揾傝暘偗傞偲丆
惵偑侾俉丆敀偑侾俇丅
僪儈僲傪晘偒媗傔傞偙偲偑偱偒傞応崌偵偼丆惵偲敀偼昁偢摨悢偲側傞偐傜丆
乻恾1乼偺椞堟傪丆僪儈僲傪晘偒媗傔傞偙偲偼偱偒側偄丅
俀丏恾偺傛偆側俙丆俛俀庬椶偺僥僩儔儈僲傪慻傒崌傢偣傞偙偲偵傛偭偰丆
乻恾俀乼偺傛偆偵惵敀岎屳偵晘偒暲傋傞偙偲偑偱偒傞丅
偙偺曽朄偱 侾侽亊侾侽 偺惓曽宍椞堟傪晘偒媗傔傞偙偲偑偱偒偨偲偡傞丅
偙偺椞堟傪 侾丏摨條巗徏柾條偵揾傝暘偗傞偲丆惵敀俆侽丅
俙 傪 倣屄丆俛 傪 値屄乮倣丆値 偼惍悢乯梡偄偨偲偡傞偲丆
僥僩儔儈僲偺憤悢偐傜丂 倣亄値亖俀俆 乧(1)
惵怓晹暘偺悢偐傜丂丂俁倣亄値亖俆侽 乧(2)
(2)亅(1) 傛傝丂丂丂 俀倣亖俀俆丂 乧乧(3)
(3)偼丆倣 偑惍悢偱偁傞偙偲偵斀偡傞丅
傛偭偰丆侾侽亊侾侽 偺惓曽宍椞堟傪丆僥僩儔儈僲偱晘偒媗傔傞偙偲偼偱偒側偄丅
夝摎丒偦偺14
乮儁儞僱亅儉丗kohji乯
栤戣1

恾偺傛偆偵偼攝怓偡傞偲丄1*2偺挿曽宍傪晘偒媗傔偨帪丄1*2偺挿曽宍堦偮偵偮偒
敀偲崟偺儅僗偑偦傟偧傟堦偮偢偮娷傑傟傞偺偱丄敀偲崟偺儅僗偼摨悢偁傞丅偟偐偟丄幚嵺偵偼敀18儅僗
丄崟16儅僗偱柕弬丅傛偭偰1*2偺挿曽宍偱晘偒媗傔傞偙偲偼弌棃側偄丅
栤戣2
 丂丂
丂丂

恾偺傛偆偵偼攝怓偡傞偲丄S傪攝抲偟偨帪丄恾偺2捠傝偑偁傝
偆傞丅晘偒媗傔偨帪偵恾偺嵍丄塃偺S偑偦傟偧傟l,r屄偁偭偨偲偡傞偲丄敀丄崟儅僗偺憤悢偵偮偄偰偦傟
偧傟丄
丂丂丂l+3r=50
丂丂丂3l+r=50
偑惉傝棫偮丅
2幃傛傝
丂丂丂l=r=12.5
偙傟偼l,r偑惍悢偱偁傞偙偲偵柕弬丅傛偭偰S偱晘偒媗傔傞偙偲偼弌棃側偄丅
夝摎丒偦偺15
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
栤戣侾
柺愊偑係偵側傞恾宍偱応崌傪峫偊傑偡丅
(1)晘偒偮傔傞偙偲偑偱偒傞椺

(2)晘偒偮傔傞偙偲偑偱偒側偄椺
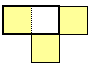
侾亊俀偺柺愊偺挿曽宍偺敿暘傪揾偭偰傒傑偡丅

偡傞偲偙偺挿曽宍偑晘偒偮傔傜傟傞応崌偵偼拝怓偝傟偨晹暘偲怓偺側偄晹暘偑摨偠屄悢偵側傝傑偡丅
儅僗栚偵壓偺傛偆偵怓傪偮偗偰傒傑偡丅
晘偒偮傔傜傟側偄応崌偵偼嘇偺傛偆偵拝怓偝傟偨晹暘偲怓偺側偄晹暘偺屄悢偑堘偄傑偡丅
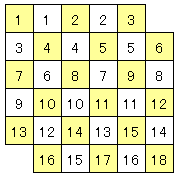
屄悢傪悢偊傞偲
拝怓偝傟偨晹暘偲怓偺側偄晹暘偺屄悢偑堎側傝傑偡丅
偩偐傜晘偒偮傔傜傟傑偣傫丅
栤戣俀
儅僗栚偵拝怓偟偰傒傑偡丅
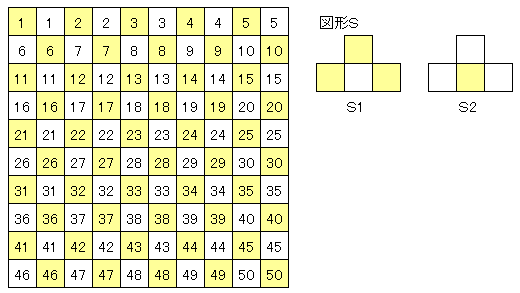
偡傞偲恾偺傛偆偵拝怓偝傟偨晹暘偲怓偺側偄晹暘偑摨偠屄悢偁傝傑偡丅
恾宍俽傪俀庬椶梡堄偟傑偡丅
恾宍俽偺柺愊偼係偱偡丅
俽1偲俽2傪岎屳偵巊偭偰晘偒偮傔偰偄偔偲偡傞偲慡晹偱俀俆屄昁梫偱偡丅
婏悢偺応崌偵偼拝怓偝傟偨晹暘偲怓偺側偄晹暘偺屄悢偑俀屄堘偄傑偡丅
偙偺栤戣偺応崌偵偼摨悢側偺偱晘偒偮傔傜傟傞昁梫忦審傪枮偨偟傑偣傫丅
偩偐傜晘偒偮傔傜傟傑偣傫丅
夝摎丒偦偺16
乮儁儞僱亅儉丗T_Tatekawa乯
栤戣1
傑偢丆1x2偺挿曽宍傪丂仩仭丂偲偄偆傛偆偵敀崟偵揾傝傑偡丏
壓塃恾偺儅僗栚傪巗徏柾條偵揾傝傑偡丏

偙偺揾傝暘偗偱丆敀偼18屄丆崟偼16屄偱偡丏
1x2偺挿曽宍偱偼敀偲崟傪1屄偢偮杽傔偰偄偔偺偱丆嵟屻偵
敀偑2屄巆偭偰偟傑偄傑偡丏偩偐傜晘偒媗傔偑弌棃傑偣傫丏
栤戣2
10x10 偺儅僗栚傪巗徏柾條偵揾傞偲丆敀偲崟偑50屄偵側傝傑偡丏
傑偨丆100儅僗傪4儅僗偺恾宍偱晘偒媗傔傞帠傪峫偊傞偲丆
25屄昁梫偱偡丏
T帤宆偺恾宍傕巗徏柾條偵揾傞偲丆

偺2僷僞乕儞偵側傝傑偡丏
敀偲崟偑摨偠悢偩偗尭偭偰峴偔傛偆偵2僷僞乕儞傪慖傇偲丆
12懳乮24屄乯慖傫偩偲偙傠偱丆10x10 偺儅僗栚偺巆傝偼
敀偲崟偑2偮偢偮偵側傝傑偡丏
忋偺2僷僞乕儞偼扨撈偱偼敀偲崟傪摨悢杽傔傞帠偑偱偒側偄
偺偱丆寢嬊偼 10x10 偺儅僗栚傪 T 帤宆偺恾宍偱晘偒媗傔傞
偙偲偼偱偒傑偣傫丏
仏仏仏
椶戣偲偟偰丆
乽4x7 偺挿曽宍傪丆7庬椶偺僥僩儕僗偺僽儘僢僋偱晘偒媗傔傜傟傞偐乿
偲偄偆偺傪丆僺乕僞乕丒僼儔儞僋儖偐傜暦偄偨帠偑偁傝傑偡丏
惓夝幰
| 僶儖僞儞惎恖 | 僆儎僕 | teki |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | T_Tatekawa | 偺偭偙傫 |
| 揮埵斀墳 | Toru | kohji |
| 嶰妏掕婯 | 柪巕偺梇擫 | 俶偲乣 |
| 忨偺偍偠偝傫 | 俽俷倀 | 怣嶰 |
| 僗儌乕僋儅儞 |
傑偲傔
奆偝傫偺夝摎偵偁傞傛偆偵丄儅僗栚傪偨偲偊偽敀崟偱揾傝暘偗偰丄
偦偺嬼婏惈乮僷儕僥傿乯傪峫偊傞偲偄偄偲偄偆栤戣偱偡偹丅
晘偒偮傔傜傟傞偙偲傪帵偡偵偼偦偺椺傪嬶懱揑偵偁偘傟偽偄偄傢偗偱偡偑丄
晘偒偮傔傜傟側偄偙偲傪帵偡偵偼丄偳傫側偙偲傪偟偰傕愨懳偵晄壜擻偱偁傞偲偄偆偙偲傪
帵偝側偗傟偽側傝傑偣傫丅
偝偰丄T_Tatekawa偝傫偺夝摎偵偁傞
乽4x7 偺挿曽宍傪丆7庬椶偺僥僩儕僗偺僽儘僢僋偱晘偒媗傔傜傟傞偐乿偲偄偆栤戣偵偮偄偰傕丄
惀旕丄峫偊偰傒偰偔偩偝偄丅
 top
top