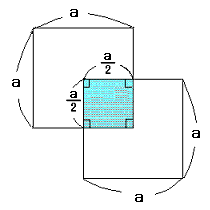
侾俀俀丏曄尪帺嵼偺恾宍
恾俙丄俛丄俠偺幬慄晹暘偺柺愊俽俙丄俽俛丄俽俠偺
戝彫娭學傪帵偟偰偔偩偝偄丅
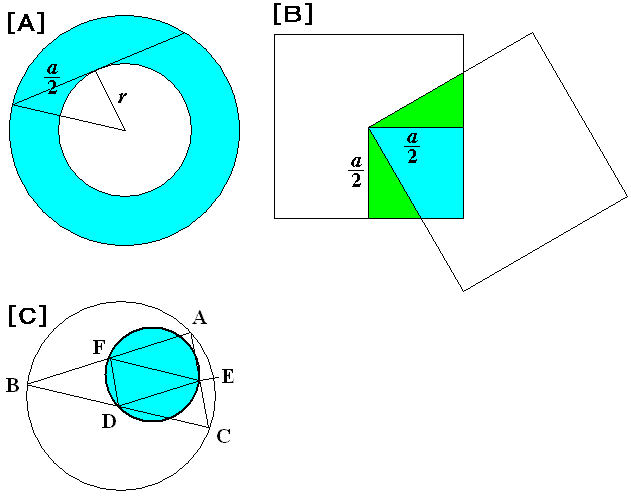
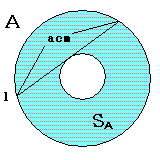 俀偮偺墌偼摨怱墌偱捈慄l偼撪晹偺墌偺愙慄
俀偮偺墌偼摨怱墌偱捈慄l偼撪晹偺墌偺愙慄
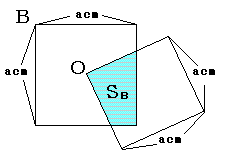 俀偮偺惓曽宍丅俷偼堦曽偺惓曽宍偺拞怱
俀偮偺惓曽宍丅俷偼堦曽偺惓曽宍偺拞怱
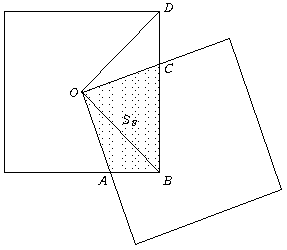
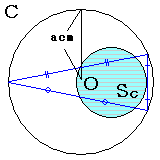 俷偼戝偒偄墌偺拞怱丅彫偝偄墌偼戝偒偄墌偵撪愙偡傞嶰妏宍偺奺曈偺拞揰傪捠傞墌
俷偼戝偒偄墌偺拞怱丅彫偝偄墌偼戝偒偄墌偵撪愙偡傞嶰妏宍偺奺曈偺拞揰傪捠傞墌
栤戣偺弌揟
敾抐椡傪崅傔傞悇棟僷僘儖
楅栘惔巑丂挊
島択幮僽儖乕僶僢僋僗
暯惉俈擭搙崙壠岞柋堳嘥庬帋尡
摎偊偲夝愢
夝摎丒偦偺1
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
摎偊丂俽俙亖俽俠亜俽俛
(1)俽俙偵偮偄偰
捈慄倢丄俙俛傪墌偺拞怱俷傪捠傞傛偆偵偡傞偲偦偺恾宍偼壓恾偺傛偆偵側傝傑偡丅
偦偟偰偦偺柺愊偼師偺捠傝敿宎a乛俀偡傞墌偺柺愊偲側傝傑偡丅
丂丂丂俽俙亖乮a/俀乯2亊兾
(2)俽俛偵偮偄偰
惓曽宍偺拞怱俷傪屌掕偟偰惓曽宍俷俧俤俥傪夞揮偝偣曈俷俧傪曈俠俢偵捈妏偵岎嵎偝偣傞偲
師偺壓恾偺傛偆偵側傝傑偡丅
偦偟偰偦偺柺愊偼師偺捠傝倎乛俀傪堦曈偲偟偨惓曽宍偺柺愊偲側傝傑偡丅
丂丂丂俽俛亖(a/2)2
(3)俽俠偵偮偄偰
墌偺屖俙俛偺拞娫揰俧傪捠傞悅捈慄偲丄屒俙俠偺拞娫揰傪捠傞悅捈慄偺岎揰偼墌偺拞怱O偲側傝傑偡丅
俛俠傪嬤偯偗傞偲壓恾偺傛偆側恾宍偵側傝傑偡丅
偦偟偰偦偺柺愊偼師偺捠傝俷俛亖a丂側偺偱俹俛傪敿宎偲偡傞墌偺柺愊偵側傝傑偡丅
丂丂丂SC=(a/2)2亊兾
廬偭偰俽俙偺柺愊乮a/俀乯2亊兾亖俽俠偺柺愊(a/2)2亊兾
亜俽俛偺柺愊(a/2)2偲側傝摎偊偼丂俽俙亖俽俠亜俽俛丂偲側傝傑偡丅
夝摎丒偦偺2
乮儁儞僱亅儉丗夝摎儖僷儞乯
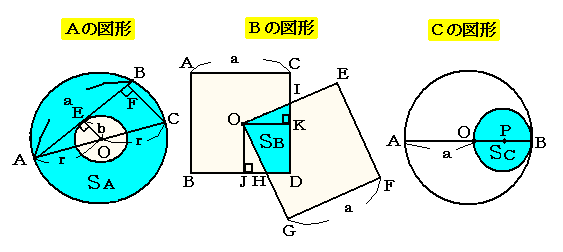
SA = 兾丒a2/4丂[cm2]
SB = a2/4 [cm2]
SC = 兾丒a2/4丂 [cm2]
亪SA 亖 SC 亜 SB
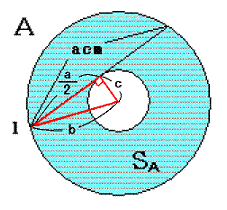
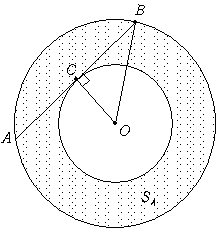
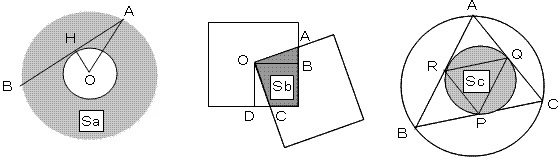
A偵偮偄偰丄撪晹偺墌偺敿宎傪 r 丄奜晹偺墌偺敿宎傪R偲偡傞丅
掙曈偺挿偝傪a偲偟偰丄墌偺拞怱傪捀揰偵擇摍曈嶰妏宍傪峫偊傞偲丄
偦偺幬曈偼奜晹偺墌偺敿宎R偵摍偟偔丄偦偺崅偝偼撪晹墌偺敿宎倰偲側傞偺偱
僺僞僑儔僗偺掕棟傛傝丄
a2/4 + r2 = R2
亪R2 - r2 = a2/4
| SA | = 兾丒R2 - 兾丒r2 |
| = 兾丒乮R2 - r2) | |
| = 兾丒a2/4丂[cm2] |
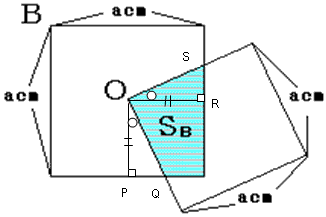
B偵娭偟偰偼丄壓偺恾偺條偵丄廳側傝偑惓曽宍偐傜彮偟偢傟偨応崌偼丄
仮OPQ佭仮ORS偲側傞乮擇妏嫴曈憡摍)偲側傞偺偱丄丂
SB偼廳側傝偑惓曽宍偺偲偒偺柺愊偵摍偟偔丄忢偵 SB = a2/4 [cm2]丂偲側傞丅
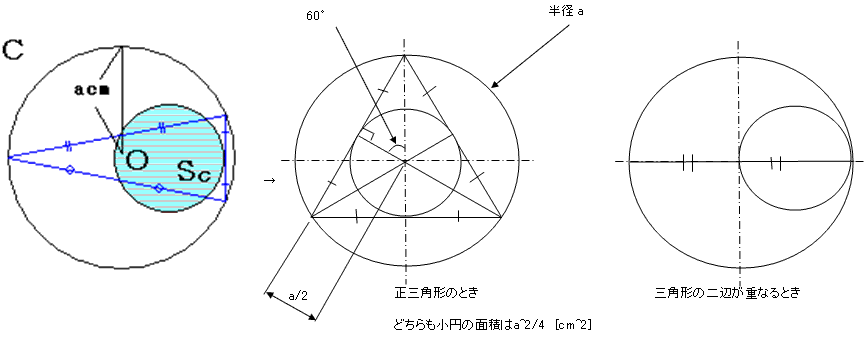
C偵娭偟偰偼堦斒揑偵峫偊傞偺偑擄偟偐偭偨偺偱丄椉嬌抂偱峫偊偰傒傑偟偨丅
傑偢丄戝墌偵撪愙偡傞嶰妏宍偺擇偮偺曈偑愙嬤偟丄嬌尷揑偵廳側偭偨偲偒傪峫偊傞偲丒丒丒
廳側偭偨擇曈偼戝墌偺捈宎偵堦抳丄傕偆堦偮偺曈偼揰偵廂懇偟偰偟傑偆偺偱丄SC偼捈宎偑戝墌偺敿宎偺墌偺柺愊偵摍偟偔側傞丅
SC = 兾丒a2/4 [cm2] 偲側傞丅
偦偺忬懺偐傜丄廳側偭偰偄偨嶰妏宍偺擇曈偺側偡妏偑戝偒偔側傝丄
嶰曈偲傕摍偟偔側偭偰惓嶰妏宍偵側偭偨偲偒傪峫偊偰傕丄
柺愊偼兾丒a2/4側偺偱丄偦傟埲奜傕摨條偲峫偊傜傟傞丅
乮捈妏偲60亱傪帩偮嶰妏宍偺幬曈偲偦偺60亱傪嫴傓曈偺斾偑俀丗侾偱偁傞偨傔乯
埲忋偺偙偲偐傜丄SA 亖 SC 亜 SB丂偲偟傑偟偨丅
夝摎丒偦偺3
乮儁儞僱亅儉丗俥倎倳倱俿乯
偦傟偧傟偺恾宍偺柺愊傪倎偱昞偟偰斾妑偡傞偺偑掕愇偱偟傚偆偐偹丅 丒丒偲偄偆偙偲偱丄弴偵専徹偟偰偄偒傑偟傚偆偐丅
亂俙亃
奜懁偺墌偺敿宎傪丂倰丄
撪懁偺墌偺敿宎傪丂倐丂偲偡傟偽丄
嶰暯曽偺掕棟傛傝丄
丂丂丂倰2亖乮倎乛俀乯2亄倐2
傑偨丄
丂丂丂俽俙亖兾倰2亅兾倐2
丂丂丂丂丂亖兾倰2亅兾乷倰2亅乮倎乛俀乯2乸
丂丂丂丂丂亖兾倎2乛係
亂俛亃
偙偆偄偆栤戣偺惈幙忋丄偳偺妏搙偱廳側偭偰傕俽俛偼忢偵堦掕側傫偱偡傛偹丠偱偁傟偽丄
俀偮偺惓曽宍偑係俆並僘儗偰廳側傞僇僞僠偱峫偊傞偲堦斣傢偐傝傗偡偄偱偡傛偹丅
偡傞偲丄俽俛偼惓曽宍偺柺愊偺係暘偺侾偵摍偟偄偐傜丄
丂丂丂俽俛亖倎2乛係
亂俠亃
偙傟傕俛偲摨條偱偡偐偹丄撪愙偡傞嶰妏宍偺忦審偼擟堄偺傛偆偱偡偐傜丄
惓嶰妏宍偱峫偊傞偺偑傢偐傝傗偡偄偱偡偹丅偡傞偲丄彫偝偄墌偺敿宎偼倎乛俀偩偐傜丄
丂丂丂俽俠亖兾乮倎乛俀乯2亖兾倎2乛係
偙傟傜傪斾妑偟偰丄
丂丂丂俽俙亖俽俠亜俽俛丂丒丒丒丒丒丒亂夝亃丂丂丂
夝摎丒偦偺4
乮儁儞僱亅儉丗傑偡傑偡僞僐偝傫乯
夝摎丗丂俽倎=俽們亜俽倐
乮斾偼丂俽倎丗俽們丗俽們亖兾丗侾丗兾丄偱偡偐丠乯
夁掱丗
俙丗俽倎亖乮戝墌偺柺愊乯亅乮彫墌偺柺愊乯偱偡丅
戝墌偺柺愊偼丄墌偺拞怱偐傜戝墌偲捈慄偺愙揰偺嫍棧偑戝墌偺敿宎乮亖俼丂偲偟傑偡乯偱丄兾俼俀丂偱偡丅
彫墌偺柺愊偼丄墌偺拞怱偐傜彫墌偲捈慄偺愙揰偺嫍棧偑彫墌偺敿宎乮亖倰丂偲偟傑偡乯偱丄兾倰俀丂偱偡丅
乮幚嵺偵偼曗彆慄傪傂偔偲暘偐傝傗偡偄偺偱偡偑乯偦偆偡傞偲丄栤戣偺倎們倣偺捈慄偲偱丄捈妏嶰妏宍偑偁傜傢傟傑偡丅
嶰暯曽偺掕棟偐傜丄乮倎乛俀乯俀亖俼俀亅倰俀偱偡丅
俽倎亖兾俼俀亅兾倰俀偱偡偐傜丄
俽倎亖兾乮俼俀亅倰俀乯
俽倎亖兾乮倎乛俀乯俀
俽倎亖兾倎俀乛係丂偵側傝傑偡丅
俛丗傑偢俽們偺晹暘偑乽惓曽宍乿偺帪偲丄乽捈妏擇摍曈嶰妏宍乿偺帪偲丄
乽偳偪傜偱傕側偄帪乿偵暘偗偰峫偊傑偡丅
乽惓曽宍乿偺帪丗丂惓曽宍俽們偺堦曈偼丂倎乛俀丂偱丄柺愊偼丂倎俀乛係丂偵側傝傑偡丅
乽捈妏擇摍曈嶰妏宍乿偺帪丗丂掙曈偑丂倎丂偱丄崅偝偑丂倎乛俀丂偲側傝丄
柺愊偼丂乮倎丒倎乛俀乯乛俀亖倎俀乛係丂偵側傝傑偡丅
乽偳偪傜偱傕側偄帪乿丗丂乮栤戣偺恾宍傪棙梡偟偰丄憡懳揑側昞尰傕巊梡偝偣偰傕傜偄傑偡乯
拞怱俷傪帩偮惓曽宍傪丂俽丂偲偟偰丄傕偆堦曽偺惓曽宍傪丂倱丂偲偟傑偡丅
拞怱俷偐傜惓曽宍俽偺塃偺曈偵悅慄傪傂偒傑偡丅
傕偆堦杮摨條偵壓偺曈偵傕悅慄傪傂偒傑偡丅
拞怱俷丄惓曽宍俽偲悅慄偺岎揰丄惓曽宍俽偲惓曽宍倱偺岎揰偺俁揰傪捀揰偲偡傞嶰妏宍偑丄俀偮偱偒傑偡丅
偦偙偱丄
丂侾丄偦傟偧傟偺悅慄偺挿偝偼摨偠偱偡丅
丂俀丄偦傟偧傟偺悅慄偲惓曽宍俽偺曈偲偺妏偼捈妏偱偡丅
丂俁丄偦傟偧傟偺悅慄偲惓曽宍倱偺堦曈偱側偡妏偼摨偠偱偡丅乮徹柧偼徣棯偝偣偰偔偩偝偄乯
備偊偵丄俀偮偺嶰妏宍偼丄堦曈偺挿偝偲偦偺椉抂偺妏搙偑摨偠側偺偱丄崌摨偱偡丅
嶰妏宍傪堏摦偡傞偲丄乽惓曽宍乿偺帪偲摨偠惓曽宍偑偱偒傑偡丅
柺愊偼丂倎俀乛係偱偡丅
俠丗偡偄傑偣傫丅偆傑偔愢柧偱偒傑偣傫丅
傑偢丄撪愙偡傞嶰妏宍偑惓嶰妏宍偺帪偼丄傕偲偺墌偺捈宎偑敿暘偺摨怱墌偵側傝傑偡丅
捈妏嶰妏宍偺帪丄幬曈偺拞揰乮墌偺拞怱乯偲捈妏偺捀揰偲偺挿偝乮傕偲偺墌偺敿宎乯傪捈宎偲偡傞墌偵側傝傑偡丅
撦妏嶰妏宍偼傕偲偺墌傛傝奜懁偵偼傒弌傑偡偑丄傗偼傝丄敿宎偑敿暘偺墌偑弌棃傑偡丅
柺愊偼敿宎偑敿暘偱偡偐傜丄俙偲摨條偵丂兾倎俀乛係偱偡丅
夝摎丒偦偺5
乮儁儞僱亅儉丗偺偭偙傫乯
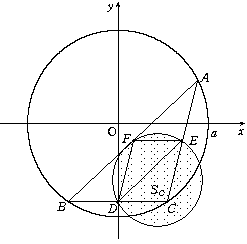
(1) 戝偒偄墌偺敿宎傪倐丄彫偝偄墌偺敿宎傪們偲偡傞
y=c 偲 x2+y2=b2 偺岎揰偺x嵗昗偼 亇併乮b2亅c2乯
2併乮b2亅c2乯=a 偩偐傜 b2-c2=a2/4
傛偭偰
丂丂丂俽俙=兾乮b2-c2乯=兾a2/4
(2) 柧傜偐偵
丂丂丂俽俛=a2/4
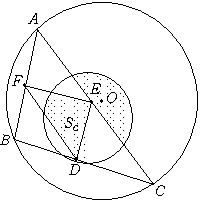
(3) 戝偒偄墌偵撪愙偡傞嶰妏宍偺捀揰傪A丄B丄C偲偡傞
AB偺拞揰傪D丄BC偺拞揰傪E丄CA偺拞揰傪F偲偡傞偲
FE:AB=1:2丄DF:BC=1:2丄ED:CA=1:2 偩偐傜
丂丂丂仮DEF佷仮CAB 乮憡帡斾1:2乯
廬偭偰仮DEF偵奜愙偡傞墌偺敿宎傪r1丄仮CAB偵奜愙偡傞墌偺敿宎傪r2偲偡傞偲
丂丂丂r1:r2=1:2丂仼偙偺曈偼榑徹偑昁梫偐傕偟傟側偄
傛偭偰
丂丂丂俽俠=兾a2/4
乮摎乯俽俙亖俽俠亜俽俛
妝偟偄栤戣偱偟偨
彫墌偵愙偡傞尫偺挿偝偑寛傑傟偽俽俙偑寛傑傞側傫偰嬃偒偱偡両
夝摎丒偦偺6
乮儁儞僱亅儉丗俶俽俹乯
俙丗擇偮偺墌偺敿宎偑捈妏嶰妏宍偺幬曈偲堦曈偺娭學側偺偱
嶰暯曽偺掕棟傛傝
丂丂丂俽倎亖兾a2/4
俛丗幬慄晹暘偼惓曽宍偺侾乛係偺僺乕僗側偺偱
丂丂丂俽倐亖a2/4
C:彫偝偄墌偺撪愙嶰妏宍偼戝偒側墌偺傕偺偺憡帡斾侾乛俀偲側偭偰偄傞丅
傛偭偰彫偝側墌偼捈宎偑a偲側傞丅
丂丂丂俽們亖兾a2/4
Sa=S們=兾a2/4亜a2/4=Sb
夝摎丒偦偺7
乮儁儞僱亅儉丗傑乕傗乯
乮摎偊乯俽俙亖俽俠亜俽俛
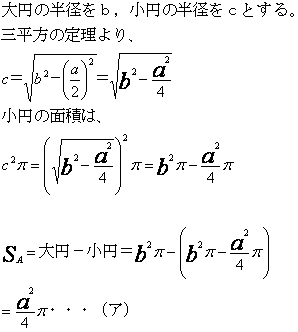


夝摎丒偦偺8
乮儁儞僱亅儉丗僥儗僗偲傾儕僗乯
乮侾乯俽俙偺柺愊傪媮傔傑偡丅
撪懁偺墌偲丄撪懁偺墌偺愙慄偲偺愙揰傪俹偲偟傑偡丅
摨怱墌偺拞怱傪俷偲偟傑偡丅
慄暘俬俷傪倶偲偟丄慄暘俹俷傪倷偲偟傑偡丅
嶰妏宍俬俹俷偼捈妏嶰妏宍偲側傝傑偡丅
倶偼奜懁偺墌偺敿宎丄倷偼撪懁偺墌偺敿宎偱偡丅
丂奜懁偺墌偺柺愊亖倶2兾 cm2
丂撪懁偺墌偺柺愊亖倷2兾 cm2
乽嶰暯曽偺掕棟乿偵傛傝丄倶2亖倷2亄乮倎/2乯2 偱偡
| 俽俙偺柺愊 | 亖 奜懁偺墌偺柺愊 亅 撪懁偺墌偺柺愊 |
| 亖 倶2兾 亅 倷2兾 | |
| 亖 (倷2亄乮倎/2乯2)兾 亅 倷2兾 | |
| 亖 乮倎/2乯2兾 cm2 |
傛偭偰丄俽俙偺柺愊偼 乮倎/2乯2兾 cm2 偱偡丅
乮俀乯俽俛偺柺愊傪媮傔傑偡丅
俀偮偺惓曽宍偺岎揰傪俹侾丄俻侾偲偟傑偡丅
俷傪拞怱偵偟偰惓曽宍傪夞揮偝偣偨帪偺怴偟偄岎揰傪俹俀丄俻俀偲偟傑偡丅
惓曽宍傪夞揮偝偣偨帪偺恾宍丄俷俹侾俹俀丄
俷俻侾俻俀 偼崌摨偲側傞偺偱
俽俛偺柺愊偼曄傢傜側偄丅
傑偨俹侾偑惓曽宍偺堦捀揰偺帪丄俻侾偼偦偺椬偺捀揰偵偁傞偺偱丄
俽俛偺柺愊偼惓曽宍偺柺愊偺巐暘偺堦偲側傝傑偡丅
傛偭偰丄俽俛偺柺愊偼 乮倎/2乯2 cm2 偱偡丅
乮俁乯俽俠偺柺愊傪媮傔傑偡丅
戝偒偄墌偵撪愙偡傞嶰妏宍傪俙俛俠偲偟傑偡丅
俙俛丄俛俠丄俠俙偺奺曈偺拞揰傪偦傟偧傟俢丄俤丄俥偲偟傑偡丅
嶰妏宍俢俤俥偼嶰妏宍俙俛俠偲崌摨偲側傝傑偡丅
嶰妏宍俢俤俥偵奜愙偡傞墌偼丄嶰妏宍俙俛俠偵奜愙偡傞墌偲崌摨偲側傝傑偡丅
偝傜偵俙偱戝偒偄墌偵撪愙偟傑偡丅
俙俛乮傑偨偼俙俠乯偑戝偒偄墌偺捈宎偺帪丄俢乮傑偨偼俥乯偼丄
戝偒偄墌偺拞怱俷偲廳側傝丄俙俷偼彫偝偄墌偺捈宎偲側傝傑偡丅
傛偭偰丄俽俠偺柺愊偼 乮倎/2乯2兾 cm2 偱偡丅
埲忋偐傜
丂丂丂俽俙 亖 乮倎/2乯2兾 cm2
丂丂丂俽俛 亖 乮倎/2乯2 cm2
丂丂丂俽俠 亖 乮倎/2乯2兾 cm2
偑媮傔傜傟傑偡丅戝彫娭學偼丄俽俙亖俽俠亜俽俛 偲側傝傑偡丅
丂摎偊丂俽俙 亖 俽俠 亜 俽俛
埲忋偱偡丅
夝摎丒偦偺9
乮儁儞僱亅儉丗怴攐恖悷挬乯
 俙
俙
塃偺恾偵偍偄偰丄戝墌偺敿宎俼丄彫墌偺敿宎傪倰偲偡傞丅
墌偺拞怱偐傜慄暘俙俛偵悅慄傪堷偔偲丄
俛俠亖a/2丂偱偁傝丄捈妏嶰妏宍俷俛俠偵偍偗傞
 俛
俛
塃偺恾偵偍偄偰丄巐妏宍俷俙俛俠偺柺愊俽俛偼丄嶰妏宍OBD偺柺愊偵摍偟偄偙偲傪帵偡丅

 俠
俠
栤戣偺戝墌傪丄尨揰拞怱丄敿宎倎偺墌偲偡傞丅
傑偨丄戝墌偵撪愙偡傞嶰妏宍俙俛俠傪丄揰俛丄俠偑倷幉懳徧偲側傞
俀揰偲偟偰傕栤戣偺堦斒惈偼幐傢傟側偄丅
偦偙偱丄俙(俀兛,俀兝)丄俛(亅俀倱,俀倲)丄俠(俀倱,俀倲)偲偡傞偲丄偙偺俁揰偼墌廃忋偺揰傛傝丄
丂丂丂係兛俀亄係兝俀亖倎俀
丂丂丂係倱俀亄係倲俀亖倎俀
偙偺俀幃傛傝丂兛俀亅倱俀亖倲俀亅兝俀丂丒丒丒(1)
彫墌偺拞怱傪媮傔傞丅
俢(侽,俀倲)丄俤(兛亄倱,兝亄倲)丄俥(兛亅倱,兝亄倲)偱偁傝丄仮俢俤俥偺奜愙墌偺拞怱偼丄
慄暘俤俥丆俢俤偦傟偧傟偺悅捈擇摍暘慄偱偁傞丅
慄暘俤俥偺悅捈擇摍暘慄偼丄倶亖倎丂丒丒丒(2)
慄暘俢俤偺悅捈擇摍暘慄

 忋偺傛偆偵丄椡媄乮戙悢妛乯偱夝摎偟偨屻偵丄娙扨暿夝乮婔壗妛丠乯傪敪尒
忋偺傛偆偵丄椡媄乮戙悢妛乯偱夝摎偟偨屻偵丄娙扨暿夝乮婔壗妛丠乯傪敪尒
俠偺亂暿夝亃
塃偺恾偵偍偄偰丄仮俙俛俠偺奜愙墌偑戝墌偱偁傞偐傜惓尫掕棟傛傝丄

埲忋俙丄俛丄俠偺寢壥傛傝丄俽俛亙俽俙亖俽俠
夝摎丒偦偺10
乮儁儞僱亅儉丗僆儎僕乯
敀偄墌偺敿宎傪倓丄傑偨堦斣戝偒側墌偺敿宎傪倢偲偡傞偲丄
媮傔傞柺愊丂俽俙偼丄
倢2兾亅倓2兾亖乮倢2亅倓2乯兾亖(兾/係)倎2
俽俙亖(兾/係)倎2丒丒丒乮侾乯
俽俛亖倎2/係丒丒丒丒乮俀乯
俽俠偼丄敿宎倎偺偵撪愙偡傞嶰妏宍偺嶰曈偺奺拞揰傪捠傞嶰妏宍偺
俁偮偺捀揰傪捠傞偐傜丄拞揰楢寢掕棟傛傝嶰妏宍偼丄憡帡斾侾乛俀偺嶰妏宍
偲側傝丂墌俽俠偼丄憡帡斾侾乛俀偺墌丂傛偭偰
俽俠亖(兾/係)倎2丒丒丒乮俁乯
乮侾乯丄乮俀乯丄乮俁乯傛傝丄俽俙亖俽俛亜俽俛
夝摎丒偦偺11
乮儁儞僱亅儉丗偵偟傗傫乯
埲壓丄挿偝偺扨埵 cm丄柺愊偺扨埵 cm2 偼徣棯偡傞
[1] 俽俙偵偮偄偰
戝偒偄墌偺敿宎傪R丄彫偝偄墌偺敿宎傪r偲偡傞偲
丂丂丂R2 = ((1/2) * a)2 + r2
丂丂亪R2 - r2 = (1/4) * a2
丂丂丂
| 俽俙 | = 兾 * (R2 - r2) |
| (1/4) * 兾 * a2 |
[2] 俽俛偵偮偄偰
堦曈偑 (1/2) * a 偺惓曽宍偺柺愊偲摍壙側偺偱
丂丂丂俽俛 = (1/4) * a2
[3] 俽俠偵偮偄偰
戝偒偄墌偵撪愙偡傞嶰妏宍偺奺曈偺拞揰傪寢傇嶰妏宍偺奺曈偺挿偝偼丄
拞揰楢寢掕棟偵傛傝丄戝偒偄嶰妏宍偺奺曈偺挿偝偺敿暘偺憡帡宍偲側傞
廬偭偰丄彫偝偄嶰妏宍傪撪愙偡傞墌偺敿宎偼丄(1/2) * a 偲側傞
丂丂丂
| 俽俠 | 兾 * ((1/2) * a)2 |
| (1/4) * 兾 * a2 |
埲忋傛傝
丂丂丂俽俙亖俽俠亜俽俛
夝摎丒偦偺12
乮儁儞僱亅儉丗nao乯
俽俙偵偮偄偰丗戝偒偄墌偺敿宎傪俼丄彫偝偄墌偺敿宎傪倰偲偡傞偲丄幬慄偺柺愊偼丄
丂丂丂俼2兾乗倰2兾亖乮俼2乕倰2乯兾 丒丒丒(1)
偙偙偱僺僞僑儔僗偺掕棟傛傝丄
丂丂丂乮倎乛俀乯2亄倰2亖俼2
丂丂丂俼2乕倰2亖倎2乛係
(1)偵戙擖偟偰
丂丂丂俽俙亖乮倎2乛係乯兾
俽俛偵偮偄偰丗俽俛偺柺愊偼倎2乛係丂乮徹柧棯乯
俽俠偵偮偄偰丗戝偒偄墌偺敿宎偼倎丅嶰妏宍偼戝偒偄墌偵撪愙偟偰偄傞偺偱丄媡偵嶰
妏宍偺奜愙墌偲峫偊傞丅
彫偝偄墌偼偦偺嶰妏宍偺奺曈偺拞揰傪捠傞偺偱丄拞揰傪寢傫偱傒傞偲丄尦偺嶰妏宍偺
敿暘偺挿偝偺憡帡嶰妏宍偵側傞偙偲偑暘偐傞丅
彫偝偄墌偼偦偺嶰妏宍偺奜愙墌偵側偭偰偄傞丅
偮傑傝丄戝偒偄墌偺敿宎偼丄彫偝偄墌偺敿宎偺俀攞偱偁傞丅
俽俠偼彫偝偄墌偺柺愊側偺偱丄
丂丂丂乮倎乛俀乯2兾亖乮倎2乛係乯兾
摎偊
丂丂丂俽俙亖俽俠亜俽俛
夝摎丒偦偺13
乮儁儞僱亅儉丗岼偺柌乯
乮恾A乯
撪晹偺彫墌偺敿宎傪倰丄奜偺戝墌偺敿宎傪R偲偡傞偲丄嶰暯曽偺掕棟偐傜
丂丂丂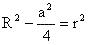 丂丂丂俽俙亖戝墌偺柺愊-彫墌偺柺愊亖
丂丂丂俽俙亖戝墌偺柺愊-彫墌偺柺愊亖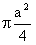
乮恾B乯
奜懁偺惓曽宍傪撪懁偺惓曽宍偺拞怱揰偱夞揮偝偣傞偲埲壓偺恾偵側傞丅
場偭偰丄柺愊丂 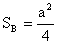
乮恾C乯
3揰偺偆偪2揰偯偮傪慖傃捈慄偱寢傃嶰妏宍傪嶌傞偲丄偦傟傜偺3曈偼慡偰傕偲偺3妏宍
偺挿偝偺敿暘偱奺乆偺曈偵暯峴側憡帡嶰妏宍偱偁傞丅偙偙偱惓尫掕棟傛傝丄
尦偺堦曈偺挿偝傪d丄偦偺捀妏傪A偲偡傞偲丄偦偺奜愙墌偺敿宎偼a偱偁傞偐傜丄
d/sinA =2a 偑惉棫偡傞丅丂3揰傪寢傫偩嶰妏宍偺偆偪d偵懳墳偡傞堦曈偺挿偝偼d/2丄
妏搙偼A偱偁傞偺偱丄
d/2sinA =2乮a/2乯偑惉棫偡傞丅懄偪丄彫墌偺敿宎偼戝墌偺敿暘偲側傞偙偲偑暘偐傞丅
場偭偰丄
丂丂丂俽俠亖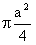
埲忋傛傝
丂丂丂俽俙亖俽俠亜俽俛偲側傞丅
夝摎丒偦偺14
乮儁儞僱亅儉丗廧媑僲昹懢榊乯
傑偢丄A偱偡丅
椉墌嫟捠偺拞怱偐傜彫墌 偺愙慄偲偺愙揰傑偱傪'b'偲偟傑偡丅
戝彫偺墌偺拞怱偼堦弿偱丄愙慄a偼
愙揰偱擇摍暘偝傟傑偡丅丂戝墌偺捈宎偼丄僺僞僑儔僗偺掕棟偱
丂丂丂( a / 2 )2 + b2 }1/2
偱偡丅丂偡傞偲幬慄晹暘偺柺愊偼丄
丂丂丂[{( a / 2 )2 + b2 }1/2]2 亊 兾 亅 b2 亊 兾
= ( a / 2 )2 亊 兾
偵側傝傑偡丅
B偱偡丅
幬慄晹暘傪O偐傜塃壓偺僇僪傊捈慄傪堷偒丄傆偨偮偺3妏宍
偵暘偗傑偡丅戝偒偄曽偺嶰妏宍偼丄傗偼傝O偐傜嵍壓偺僇僪傊捈
慄傪堷偄偰丄彫偝偄曽偺嶰妏宍偺塃偵尰傟傞嶰妏宍偲乫崌摨乫偱偡丅丂
側偤側傜丄侾曈乮懳妏慄偺敿暘乯偲俀妏乮45搙偲拞怱晹暘偺妏乯
偑堦弿偩偐傜偱偡丅丂廬偭偰丄幬慄晹暘偺柺愊偼
丂丂丂a亊 ( a / 2 ) / 2= ( a / 2 )2
C偱偡丅
偍偍偒偄墌偼嶰妏宍偺奜愙墌丄拞偺彫偝偄墌偼傕偲偺嶰妏宍偺憡帡宍偱
敿暘偺戝偒偝偺嶰妏宍偺奜愙墌偩偐傜丄偍偍偒偄墌偺捈宎偑a偩
偲彫偝偄墌偺捈宎偼a/2丅丂幬慄晹暘偺柺愊偼丄
丂丂丂( a / 2 )2 亊 兾
摎偊丂SA 亖 SC 亜 SB
夝摎丒偦偺15
乮儁儞僱亅儉丗恀壞偺僒儞僞乯
嶰暯曽偺掕棟傪巊偆偲丄
丂丂丂戝偒偄墌偺敿宎偺俀忔乕彫偝偄墌偺敿宎偺2忔亖a2/ 4
偲側傞偺偱丄幬慄晹偺柺愊偼a2/4亊兾偲側傝傑偡丅
B偼摍愊曄宍偱偪傚偆偳丄惓曽宍偺柺愊偺侾/係偵側傞偺偱幬慄晹偺柺愊偼a2/4
C偵偮偄偰丅戝偒偄3妏宍偲丄拞揰傪寢傫偱偱偒傞3妏宍偼憡帡偵側傝丄憡帡斾偼侾丟
俀偱偡丅偦偺偨傔柺愊斾偼侾丟係丏戝偒偄墌偺柺愊偼a2亊兾側偺偱丄彫偝偄墌偺柺
愊偼a2/4亊兾丅
備偊偵幬慄晹偺柺愊偼C亖A亜B偲側傝傑偡丅
夝摎丒偦偺16
乮儁儞僱亅儉丗To the stars乯
仭S(A)偺柺愊傪媮傔傞
奜懁偺墌偺敿宎傪兛丄撪懁偺墌偺敿宎傪兝偲偍偔偲丄
嶰暯曽偺掕棟傛傝丄
丂丂丂(兛2)-(兝2)=(a/2)2
偑惉傝棫偮丅
丂丂丂
| S(A) | =兾(兛2)-兾(兝2) |
| =兾{(兛2)-(兝2)} | |
| =兾(a/2)2 | |
| =(兾a2)/4 |
仭S(B)偺柺愊傪媮傔傞
O傪拞怱偲偟偨惓曽宍偵偍偄偰丄O傪捠傞悈暯慄偲悅慄傪堷偔偲丄
S(B)偼丄戜宍偲捈妏嶰妏宍偵暘抐偝傟傞丅
偙偺偆偪捈妏嶰妏宍偺曽偼丄斀懳懁偺捈妏嶰妏宍偺晹暘偲崌摨
偱偁傞偨傔丄
丂丂丂
| S(B) | =(a/2)(a/2) |
| =(a2)/4 |
仭S(C)偺柺愊傪媮傔傞
墌O偺撪愙嶰妏宍傪嶰妏宍A偲偡傞丅
嶰妏宍A偺妏曈偺拞揰傪慡偰捠傞墌傪墌P偲偡傞丅
嶰妏宍A偺妏曈偺拞揰傪慡偰捠傞嶰妏宍傪嶰妏宍B偲偡傞丅
偙偺帪丄嶰妏宍B偼墌P偺撪愙嶰妏宍偱偁傞偙偲偼柧傜偐偱偁傞丅
傑偨丄嶰妏宍偺拞揰楢寢掕棟偵傛傝丄嶰妏宍A偲嶰妏宍B偼憡帡偱偁傝丄
懳墳偡傞奺曈偺斾偼2:1偱偁傞偙偲傕柧傜偐偱偁傞丅
嶰妏宍A偼墌O偺撪愙嶰妏宍偱偁傝丄
嶰妏宍B偼墌P偺撪愙嶰妏宍偱偁傞偐傜丄
墌O偺敿宎a偲墌P偺敿宎傕2:1偱偁傞丅
傛偭偰丄墌P偺敿宎偼(a/2)偱偁傞丅
丂丂丂
| S(C) | =兾(a/2)2 |
| =(兾a2)/4 |
埲忋偵傛傝丄
丂丂丂S(B) 亙 S(A) 亖 S(C)
夝摎丒偦偺17
乮儁儞僱亅儉丗僶儖僞儞惎恖乯
摎偊俽俙亖俽俠亜俽俛
俙丗彫偝偄墌偺敿宎傪倐偲偡傞偲戝偒側墌偺柺愊偼
丂丂丂兾乮倎2/係亄倐2乯
偙偙偐傜彫偝偄墌偺柺愊兾倐2傪堷偔偲
丂丂丂兾倎2/係
俛丗揰俷偐傜塃曈媦傃掙曈偵悅慄傪堷偄偰偱偒傞
嶰妏宍偼摍偟偄偺偱幬慄晹偼1/4偺惓曽宍偵摍偟偄丅
備偊偵
丂丂丂倎2/係
俠丗嶰妏宍偺拞揰傪寢傫偱偱偒傞嶰妏宍偼拞揰楢寢掕棟傛傝丄
奺曈偑尦偺嶰妏宍偺1/2偲側傝丄憡帡斾1/2偺憡帡嶰妏宍偲側傞丅
戝偒側墌丄彫偝側墌偼丄奺嶰妏宍偺奜愙墌偩偐傜彫偝側墌偺
敿宎偼戝偒側墌偺敿宎偺1/2丅備偊偵彫偝側墌偺柺愊偼
丂丂丂兾倎2/係
乮惓捈偵怽偟傑偡偲丄俠偼嵗昗宯偐傜椡傑偐偣偵夝偄偰丄
敿宎a/2傪媮傔丄偦偙偐傜忋偺夝朄傪巚偄偮偒傑偟偨乯
夝摎丒偦偺18
乮儁儞僱亅儉丗揮埵斀墳乯
俙偵偮偄偰
戝偒偄墌偺敿宎傪俼丄彫偝偄墌偺敿宎傪倰偲偡傞偲丄
俽俙亖兾乮俼2亅倰2乯
嶰暯曽偺掕棟偐傜丄俼2亅倰2亖乮倎乛俀乯2側偺偱
俽俙亖兾倎2乛係
俛偵偮偄偰
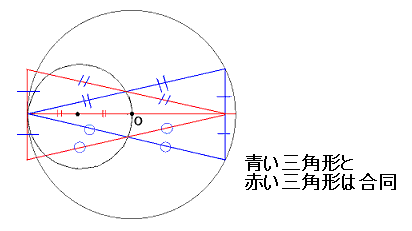
壓恾偺捠傝丄幬慄晹暘偺堦晹偱偁傞仮OPQ偵偮偄偰
仮OPQ佭仮ORS側偺偱
俽俛偼堦曈偑倎乛俀偺惓曽宍偺柺愊偵摍偟偄
俽俛亖倎2乛係
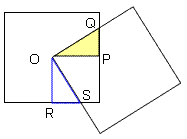
俠偵偮偄偰
戝偒偄墌偵撪愙偡傞嶰妏宍傪仮俹俻俼偲偟丄
奺曈偺拞揰傪寢傫偱偱偒傞嶰妏宍傪仮倃倄倅偲偡傞偲
拞揰楢寢掕棟偐傜丄仮倃倄倅佷仮俹俻俼丄偦偺憡帡斾偼侾丗俀
仮倃倄倅偼彫偝偄墌偵撪愙偡傞嶰妏宍偱偁傞偙偲偐傜丄
彫偝偄墌偲戝偒偄墌偺憡帡斾傕侾丗俀
傛偭偰丄俽俠亖兾倎2乛係

埲忋偺寢壥偐傜丄俽俙亖俽俠亜俽俛
夝摎丒偦偺19
乮儁儞僱亅儉丗T_Tatekawa乯
A: 戝偒偄墌偺敿宎傪 R[cm], 彫偝偄墌偺敿宎傪 r[cm] 偲偡傞偲丆
丂丂丂R俀=(a/2)俀+r俀
幬慄晹偺柺愊偼
丂丂丂兾(R俀 - r俀) = 兾a俀/4 [cm俀]
B: O 傪捀揰偺堦偮偲偡傞惓曽宍偼丆O 傪拞怱偲偡傞惓曽宍偲
岎傢傞偑丆偙傟偵傛偭偰慜幰偵娷傑傟傞屻幰偺曈偺挿偝偼 崌寁偱 a[cm] 偱偁傞丏
曗彆慄傪堷偔偙偲偵傛傝幬慄晹偼崅偝 (a/2) [cm] 偺
擇偮偺嶰妏宍偵暘妱偱偒傞偺偱丆幬慄晹偺柺愊偼
丂丂丂a*a/2 /2 = a俀/4 [cm俀]
C: 彫偝偄墌偼嶰妏宍偺拞揰傪捠傞偺偱丆撪愙偡傞嶰妏宍偼
戝偒側墌偵撪愙偡傞嶰妏宍偲憡帡娭學偵偁傝丆偐偮
憡帡斾偑 1:2 偱偁傞偙偲傪巊偄傑偡丏
偡傞偲彫偝偄墌偺敿宎偼 a/2 側偺偱丆幬慄晹偺柺愊偼
丂丂丂兾(a/2)俀 = 兾a俀/4 [cm俀]
傛偭偰柺愊偺戝彫娭學偼 SA 亖 SC 亜 SB 偱偁傞丏
夝摎丒偦偺20
乮儁儞僱亅儉丗嶰妏掕婯乯
乵俙乶 彫墌偺敿宎傪 r 偲偡傞偲戝墌偺敿宎偼 併(a2/4亄r2)
丂丂亪 SA亖兾(a2/4亄r2)亅兾r2亖兾a2/4
乵俛乶 恾偺墿椢偺嶰妏宍偺柺愊偑摍偟偄偐傜丆
丂丂丂SB亖(a/2)2亖a2/4
乵俠乶 俁曈偺拞揰傪 D丆E丆F 偲偡傞偲丆
拞揰楢寢掕棟傛傝 DE亖AB/2丆EF亖BC/2丆FD亖CA/2 偱 仮DEF佷仮ABC丅
俁揰 D丆E丆F 傪捠傞墌偼 仮DEF 偺奜愙墌偱丆偦偺敿宎偼柧傜偐偵 a/2丅
丂丂亪 SC亖兾a2/4
埲忋傛傝丂SA亖SC亜SB
夝摎丒偦偺21
乮儁儞僱亅儉丗Toru乯
A丂戝偒偄曽偺墌偺敿宎R丂彫偝偄曽偺墌偺敿宎r偲偡傞偲
丂丂丂R2-r2=(a/2)2
傛傝
丂丂丂俽俙=兾(R2-r2)=兾a2/4 (cm2)
B丂巐妏宍俽俛傪O傪捠傞懳妏慄偱俀偮偺嶰妏宍偵暘妱偟曅曽傪俋侽搙夞揮偡傞偲丂
俽俛偼
惓曽宍偺侾乛係偱偁傞偙偲偑暘偐傞偺偱
丂丂丂俽俛=a2/4 (cm2)
C丂嶰妏宍偺奺曈偺拞揰傪寢傫偩嶰妏宍偼傕偲偺嶰妏宍偲憡帡偱憡帡斾偼俀丗侾
俽俠偼偦偺嶰妏宍偺奜愙墌偱敿宎偼傕偲偺墌偺侾乛俀偲側傞偺偱
丂丂丂俽俠=兾a2/4 (cm2)
埲忋傛傝俽俙亖俽俠亜俽俛
夝摎丒偦偺22
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
俽俙偺柺愊偼丄戝偒偄墌偺敿宎傪R丄彫偝偄墌偺敿宎傪倰偲偡傞偲丄
丂丂俽俙亖兾(俼2亅倰2)丂偱偡丅
俽俙偺恾偱丄仮O俙俫偵僺僞僑儔僗偺掕棟傪巊偆偲丄
丂丂俼2亖倰2亄(倎乛俀)2丂傛傝
丂丂俼2亅倰2亖倎2乛係丂丂側偺偱
丂丂俽俙亖兾丒倎2乛係
俽俛偺柺愊偼丄恾偺傛偆偵仮俷俙俛佭仮俷俠俢側偺偱
尦偺惓曽宍偺侾乛係偺戝偒偝偱偡丅
丂丂俽俛亖倎2乛係
俽俠偺柺愊偼丄戝偒偄墌偺侾乛係偱偡丅
戝偒偄墌偼丄仮俙俛俠偺奜愙墌偱偡丅
彫偝偄墌偼丄仮俹俻俼偺奜愙墌偱偡丅
嶰妏宍偺拞揰楢寢掕棟傛傝擇偮偺嶰妏宍偼憡帡偱
憡帡偺斾偼俀丗侾偱偡丅
偩偐傜柺愊偺斾偼係丗侾偱偡丅
丂丂俽俠亖兾丒倎2乛係
側偺偱丄俽俙亖俽俠亜俽俛丂偲側傝傑偡丅
夝摎丒偦偺23
乮儁儞僱亅儉丗抴鍋偺憙忛乯
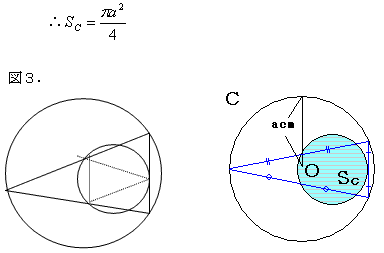
俙丏摨怱墌偺彫墌偵愙偡傞戝墌偺尫偺挿偝丂倎噋
恾侾丏偺傛偆偵俀偮偺捈妏嶰妏宍偑惗偢傞丅
戝墌丄彫墌偦傟偧傟偺敿宎傪丂俼噋丄倰噋丂偲偡傟偽僺僞僑儔僗偺掕棟偐傜
丂丂丂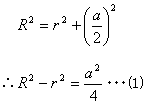
偲偙傠偱
丂丂丂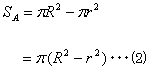
(1)(2)傛傝丂
丂丂丂
俛丏恾俀丏1偐傜恾俀丏3傑偱斀帪寁夞傝偵堦曽偺惓曽宍傪夞揮偝偣傞丅 廳側傞柺愊偺丄幐傢傟傞晹暘偲摼傜傟傞晹暘偲偑摍偟偄丅乮懳徧惈偐傜柧敀偲尵偭偰傛偄偱偡偐乯 廬偭偰
俠丏恾俁丏偺戝嶰妏宍偺奺曈偺拞揰傪寢傫偱彫嶰妏宍傪偮偔傞丅拞揰楢寢掕棟偐傜戝彫嶰妏宍偺憡帡斾偼俀丗侾丅 戣堄偐傜戝墌偼戝嶰妏宍偺丄彫墌偼彫嶰妏宍偺奜愙墌偩偐傜戝彫偺墌偺憡帡斾傕俀丗侾丅柺愊斾偼係丗侾丅
俙丏俛丏俠丏偐傜摼傜傟傞寢榑丟
丂丂丂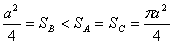
惓夝幰
| 恀壞偺僒儞僞 | 偵偟傗傫 | 岼偺柌 |
| To the stars | Toru | 栭傆偐偟偺偮傜偄偍偠偝傫 |
| 偺偭偙傫 | 揮埵斀墳 | 傑偡傑偡僞僐偝傫 |
| 僆儎僕 | 怴攐恖悷挬 | 夝摎儖僷儞 |
| 忨偺偍偠偝傫 | nao | 僥儗僗偲傾儕僗 |
| 廧媑僲昹懢榊 | T_Tatekawa | 傑乕傗 |
| 俶俽俹 | 嶰妏掕婯 | 俥倎倳倱俿 |
| 僶儖僞儞惎恖 | 抴鍋偺憙忛 |
傑偲傔
偙偺栤戣偵搊応偡傞恾宍偼丄偳傟傕曄尪帺嵼丄帵偝傟偨忦審傪枮偨偟側偑傜堏摦偝偣偰傕丄
柺愊偼曄壔偟傑偣傫(*)丅偱偡偐傜丄嬌抂側忬懺偱柺愊傪媮傔傞偙偲偑偱偒傑偡丅
恾俙偺応崌丄撪懁偺墌偺敿宎傪偳傫偳傫彫偝偔偟偰侽偱峫偊傞丄
恾俛偺応崌偼丄俀偮偺惓曽宍傪暯峴堏摦偺埵抲偱峫偊傞丄
恾俠偺応崌偼丄撪愙偡傞嶰妏宍傪惓嶰妏宍偱峫偊偨傝丄侾曈偺挿偝傪抁偔偟偰侽偱峫偊傞側偳偱偡丅
偨偩偟丄尩枾偵偄偊偽丄(*)傪徹柧偟側偗傟偽側傝傑偣傫偑丄懡偔偺曽偑徹柧傪娷傔偰夝摎偟偰偔偩偝偄傑偟偨丅
恾俙偵偮偄偰偼丄栤戣21丂偠傘偆偨傫偺栤戣偱庢傝忋偘偨僥乕儅偱偡偑丄 偍傕偟傠偄惈幙偱偡傛偹丅
 top
top