Weekend Mathematics／問題／問題21

２１．じゅうたんの問題

タックじゅうたん株式会社は、 新空港の輪状の回廊の床にじゅうたんを敷く 仕事を請け負いました。
タック社長はその計画書をみて怒りだしてしまいました。 それには、内側の壁に接した弦の長さだけしか 書いていなかったからです。

タック氏：めちゃめちゃだよ。 ２つの円の間の輪になっている 部分がどのくらいあるのかわからないじゃあ、 見積もれやしないよ。 いったいどうしろというのだろう。 デザイナ−のシャ−プさんのところへ行って相談してみよう。

シャ−プ氏はすぐれた幾何学者であり、きわめて冷静な人です。

シャ−プ氏：タックさん、その弦の長さこそ私が知りたかった ただ１つの長さなんですよ。 私の公式にそれをあてはめて輪になっている部分の面積をだしてみましょう。

タック社長は一瞬驚きましたが、すぐに笑顔をとりもどしました。

タック氏：シャ−プさん、どうもありがとう。 でもあなたも、あなたの公式もいらないことがわかりましたよ。 ２つの円が示す部分を知る必要はないのです。 結果は．．．？。

さて、タック氏はどう考えたのでしょう？　 また、じゅうたんの面積は？

解答・その１

（ペンネ−ム：akihiro）

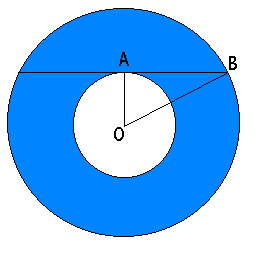
図のように点Ｏ・Ａ・Ｂを定めます。
三平方の定理より、
ＡＢ^２＋ＡＯ^２＝ＢＯ^２ ということがわかります。
つまり、ＡＢ＝１００÷２で５０
５０^２＝２５００
２５００＋ＡＯ^２＝ＢＯ^２
ＢＯ^２−ＡＯ^２＝２５００★

次に面積との関係を考えてみますと、
小さい円（白）の面積がＡＯ^２π、
大きい円（青＋白）の面積がＢＯ^２πなので、
青い部分の円の面積はＢＯ^２π−ＡＯ^２π
まとめるとπ（ＢＯ^２−ＡＯ^２） であることがわかります。

こうなりますともう簡単です。 ★の式より、求める答えは２５００πです。

いかがでしょうか。授業中サボって考えました（笑）

解答・その２

（ペンネ−ム：マサボー）

外円の半径をａ、内円の半径をｂとすると、
求める面積はπ(ａ^２ーｂ^２)となる。
いま、円の中心（Ｏとする）より接点（Ａとする）へ垂線を下ろすと、 その長さは内円の半径ｂである。
また、中心から外円の接線開始点（Ｂとする） への距離は外円の半径ａと等しい。
線ＢＡは接線であるため、∠ＢＡＯは垂直となり、 三角形ＢＡＯは直角３角形であり、 その長さは５０m（１００／２）であることから、
５０^２＋ｂ^２＝ａ^２
ａ^２ーｂ^２＝５０^２＝２５００
よって求める面積は２５００π ｍ^２である。

多分、これはシャープ氏が考えたことでしょう。 さて、タック氏は。。。。

タック氏の考え

別に内円を考える必要がなく （外円の半径をa、内円の半径をbとして a²-b²=50²が 成り立つ限り、内円の面積の増加した分、 外円の面積は同じだけ増えるので）、b=0 として半径50mの円を考え、求める面積は2500π m²

解答・その３

（ペンネ−ム：Hungry Bear）
シャ−プ氏の考えは

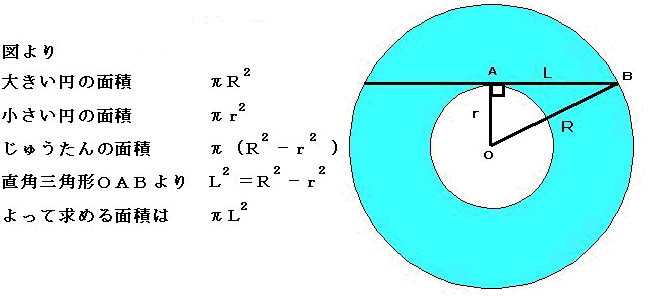
タック氏の考えは
「１００ｍを円の直径と考え、その面積を計算すればよい」
と言うことになります。

面積　　3.14×(100/2)×(100/2)≒7850 (平方メートル)

解答・その４

（ペンネ−ム：Idaho Potato）

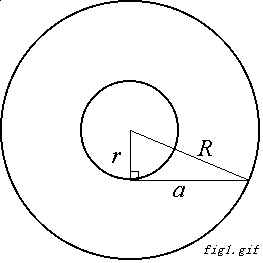
問題の原文は物語調で書かれていますが、ここでは、単純に

fig1.gif において、2つの円に挟まれたドーナツ形の領域の面積は、 長さ a のみに依存して決まることを証明せよ。

(1) スタンダードな解法

ピタゴラスの定理より、

a² = R² - r²

πR² - πr²
= π(R² - r²)
= πa²

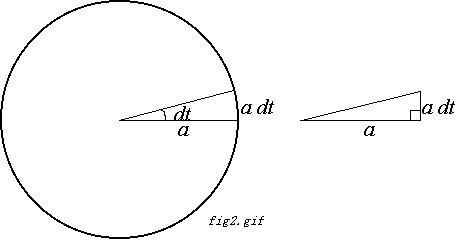
(2) 積分を使った解法

上の結果を見ると、求める面積は、実は、 半径 a の円の面積に等しいことがわかります。
この事実をさらにわかりやすく示すために、 題意の面積を積分を使って求めることを考えます。
(極限に関する厳密な議論は省略して、大雑把に考え方を述べます。)

まず、半径 a の円については、fig2.gif のように、 中心角 dt の扇形に細分することを考えます。
dt が十分小さいとき、この扇形は、 底辺 a 、高さ a dt の直角三角形とみなすことができて、 その面積は a² dt / 2 です。
これを t = 0 〜 2π で積分して、 求める面積は πa² となります。

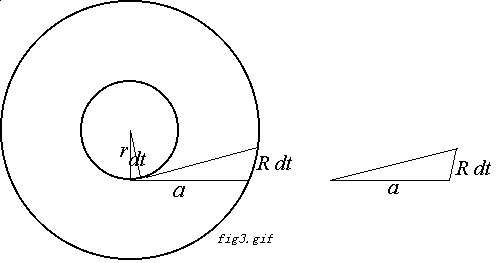
問題のドーナツ形については、 fig3.gif のような細分を考えます。
これも、dt が十分小さいとき、個々の細分は、 図の右のような三角形とみなすことができます(*)。
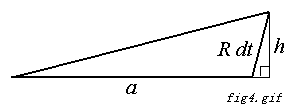
この三角形の底辺を a としたときの高さを h とすると、 fig4.gif において、右側の小さな直角三角形が、 fig1.gif に現れる直角三角形と相似である(**)ことから、 h = a dt であることがわかります。
したがって、個々の細分の面積は、 やはり a² dt / 2 であり、 題意の面積は、これを t = 0 〜 2π で積分して、 πa² となります。

簡単に言うと、

円を「細かい直角三角形を積み上げたもの」と考えたとき、 その直角三角形を(面積を変えずに)変形して鈍角三角形にして、 上手に積み上げていくと、同じ面積のドーナツ形ができる、

(*) 外側の円弧の長さが R dt であることの説明: dt = 2π/n の場合は、円周 2πR の 1/n となるので、OK。
したがって、dt = 2π×(有理数) の場合はすべてOK。
無理数は有理数の極限で表せることと、連続性を考えると、 dt がどんな実数であってもOKとなる。

(**) fig4.gif の右の小さな直角三角形の、左下の角に注目します。 斜辺が大円の接線に対応することと、 接線はその点を通る半径に垂直であることを考えると、 この角は、fig1.gif に現れる直角三角形の左上の角に 等しいことがわかります。

まとめ

タック社長は次のように考えたのです。
内側の円に外接している弦の長さだけがわかっているときに、 リングの面積を出すような公式が存在しているのだろう。 言い換えれば、弦の長さを変えなければ、どんな半径の２つの円でも かまわないということだ。
ならば、内側の円の半径が、その最小限の長さ、 つまり０になったとしてもいいわけだ。 この場合、リングは１つの円になってしまい、 直径は100mの弦の長さと同じになります。
一般に、リングの面積は、リングの内部にひくことのできる 最長の長さを直径とする円の面積に等しいということができます。

さて、右の図のように形の異なるド−ナッツ状(境界は同心円) のクッキ−が２個あります。 どちらが大きいか調べるには、糸が１本あれば充分ですね。
もちろんクッキ−の厚さは同じとします。

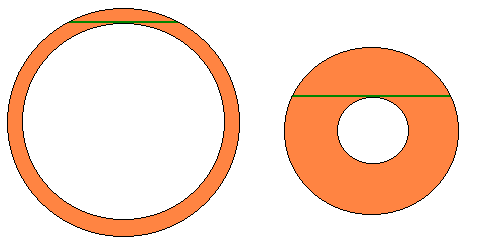
内側の円に接した弦の長さを比較すればいいわけです。 右のクッキ−の方が大きいというわけです。

右の図のような円筒形のパイプ本体の容積を出す時にも 応用できます。
パイプの断面にひける最長の線の長さがわかれば、 断面積を求めることができ、 それにパイプの長さをかければいいわけです。

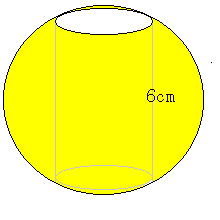
球体の真ん中に円筒形の穴がまっすぐ開けられています。 穴の長さは6cmです。 残された部分の体積はどれくらいでしょうか？

この問題でも、もう少しほかの値がなくては その削りとられなかった部分の体積を決めるのは無理のようにみえます。 ところが計算なしで、 この部分の体積が穴の長さと同じ直径をした球体の体積とつねに同じで あることが示されるのです。

もし、穴の長さだけでこの問題の答えが得られたとすると、 穴をあけたあとに残された部分の体積は、 穴の直径とは無関係でなければならないはずです。 そこで、穴の直径をその最低限度である０まで小さくしてみると、 穴の長さは球体の直径を示す直線になってしまいます。

半径ｒの球体の体積は(4/3)πｒ^３ですから、
問題の立体の体積は(4/3)π３^３＝３６πcm^３ となります。

では、この立体の体積を求めるのに、穴の長さだけが必要な値であることを 示しましょう。
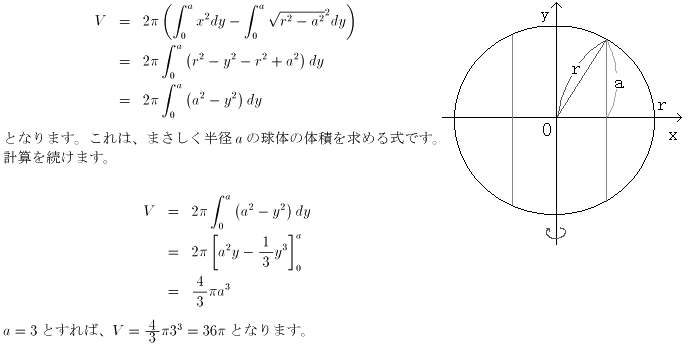
球の半径をｒ、穴の長さを２ａとして考えてみます。
回転体の体積として積分で求めます。

戻る