侾俀侽丏嶰妏宍偑偱偒傞妋棪
10cm偺恓嬥偑偁傝丄擟堄偵俀揰傪偲偭偰俁杮偵愗抐偡傞丅 偙偺偲偒俁杮偺恓嬥偱嶰妏宍偑偱偒傞妋棪偼偳傟偩偗偐丅
栤戣偺弌揟
敾抐椡傪崅傔傞悇棟僷僘儖
楅栘惔巑丂挊
島択幮僽儖乕僶僢僋僗
摎偊偲夝愢
夝摎丒偦偺1
乮儁儞僱亅儉丗傑偡傑偡僞僐偝傫乯
夝摎丗丂侾乛係偺乮傕偟偔偼丄侾乛係偵尷傝側偔嬤偄乯妋棪偱嶰妏宍偑偱偒傞丅乮偱偟傚偆偐丠乯
夁掱丗丂傑偢丄朄懃傪尒偮偗傞偺偵丄侾cm扨埵偱愗偭偨応崌傪峫偊傑偟偨丅乮偡偄傑偣傫丒丒丒巹偼偪偐傜傢偞偱乯
侾亅侾亅俉丄侾亅俀亅俈丄丒丒丒丄俀亅侾亅俈丄丒丒丒丄俉亅侾亅侾丂偲丄
擟堄偺俀揰傪愗偭偨応崌偵侾cm扨埵偺応崌丄俁俇捠傝峫偊傜傟傑偡丅
乮偙偺峫偊曽偱偄偄偱偡傛偹偊丠偨偲偊偽丄
侾亅侾亅俉丄侾亅俉亅侾丄俉亅侾亅侾偼擟堄偺俀揰偼恓嬥偺偳偪傜偐堦曽偺抂偐傜
侾偲俀丄侾偲俋丄俉偲俋丄cm偺埵抲偱愗抐偡傞偲偄偆峫偊曽偱丒丒丒丅乯
偱丄乽嶰妏宍乿偑偱偒傞忦審傪峫偊傞偲丄偙偺栤戣偺応崌丄
俁杮偺愗抐偟偨恓嬥偺偆偪丄俆cm埲忋偺恓嬥偑側偄偙偲偵側傝傑偡丅
乮俁曈偺偆偪堦斣挿偄侾曈偺挿偝偑巆傝俀曈偺挿偝偺榓傛傝抁偄偙偲乯尵偄姺偊傞偲丄
俁杮偺恓嬥偑偡傋偰俆cm枹枮偱側偄偲嶰妏宍偵偼側傝摼側偄丄偲尵偆偙偲偵側傝傑偡丅
偦偙偱丄嶰妏宍偑偱偒傞忦審傪侾cm扨埵偱峫偊偨応崌乮俁杮偲傕俆cm枹枮乯偼丄
俀亅係亅係丄俁亅俁亅係丄俁亅係亅俁丄係亅俀亅係丄係亅俁亅俁丄係亅係亅俀偺俇捠傝偱偡丅
偱偡偐傜丄妋棪偼丂俇乛俁俇亖侾乛俇丂偱偡丅
師偵丄侾mm扨埵偱峫偊傑偟偨丅乮偡偄傑偣傫丅偙傟傕偪偐傜傢偞偱偡丅乯
侾亅侾亅俋俉丄侾亅俀亅俋俈丄丒丒丒丄俀亅侾亅俋俈丄俀亅俀亅俋俇丄丒丒丒丄
俋俈亅俀亅侾丄俋俉亅侾亅侾丂偲丄嵍偺悢帤偑丂侾丂偺偲偒俋俉捠傝丄
俀丂偺偲偒俋俈捠傝丄俁丂偺偲偒俋俇捠傝丄丒丒丒丄俋俉丂偺偲偒侾捠傝丂偲側傝丄
慡晹偱丂係俉俆侾乮丂亖俋俉乮俋俉亄侾乯乛俀丂乯捠傝偵側傝傑偡丅
摨條偵俁偮偺悢帤偑偡傋偰俆侽枹枮傪扵偡偲丄嵍偺悢帤偑丂侾丂偺偲偒侽捠傝丄俀偺偲偒侾捠傝丄
俁丂偺偲偒俀捠傝丄係丂偺偲偒俁捠傝丄丒丒丒丄係俋丂偺偲偒係俉捠傝丄
俆侽丂偺偲偒侽捠傝丄俆侾丂偺偲偒侽捠傝丄丒丒丒丄俋俉丂偺偲偒侽捠傝丂偲側傝丄
嶰妏宍偵側傝摼傞応崌偼丂侾侾俈俇乮丂亖係俉乮係俉亄侾乯乛俀丂乯捠傝偵側傝傑偡丅
嶰妏宍偵側傞妋棪偼丂侾侾俈俇乛係俉俆侾亖俀係乛俋俋亖俉乛俁俁丂偱偡丅
偪傚偭偲尒偊偰偒偨傛偆側偒偑偟傑偡丅
師偵侽丏侾mm扨埵偱峫偊傑偟偨丅
崱搙偼侾侽侽侽暘妱偵側傝傑偡丅忋乮侾侽侽暘妱乯偲摨條偵峫偊丄嵍偺悢帤偑丂
侾丂偺偲偒俋俋俉捠傝丄俀丂偺偲偒俋俋俈捠傝丄俁丂偺偲偒俋俋俇捠傝丄丒丒丒丄偱丄
慡晹偱丂係俋俉俆侽侾乮丂亖俋俋俉乮俋俋俉亄侾乯乛俀丂乯捠傝偵側傝傑偡丅
俁偮偺悢帤偑偡傋偰俆侽侽枹枮傪扵偡偲丄嵍偺悢帤偑丂侾丂偺偲偒侽捠傝丄
俀丂偺偲偒侾捠傝丄丒丒丒丄係俋俋丂偺偲偒係俋俉捠傝丄俆侽侽丂偺偲偒侽捠傝丄丒丒丒丄
俋俋俉丂偺偲偒侽捠傝丂偲側傝丄嶰妏宍偵側傝摼傞応崌偼丂
侾俀係俀俆侾乮丂亖係俋俉乮係俋俉亄侾乯乛俀丂乯捠傝偵側傝傑偡丅
嶰妏宍偵側傞妋棪偼丂侾俀係俀俆侾乛係俋俉俆侽侾亖俀係俋乛俋俋俋亖俉俁乛俁俁俁丂偱偡丅
偝偰丄愭偱偼幃傪峫偊傑偣傫偱偟偨偑丄侾侽暘妱偺偲偒偼慡晹偱丂俁俇乮丂亖俉乮俉亄侾乯乛俀丂乯捠傝偱丄
嶰妏宍偵側傝摼傞応崌偼丂俇乮丂亖俁乮俁亄侾乯乛俀丂乯捠傝偱偡丅
妋棪偼忋偱傕彂偄偨傛偆偵丄俇乛俁俇亖侾乛俇丂偱偡丅
侾侽侽暘妱丄侾侽侽侽暘妱偺偲偒偺條偵丄暘曣傪乽俋乿偩偗偱昞尰偡傞偲丄
侾侽暘妱偺偲偒偼丂侾丏俆乛俋丂偲側傞丅
妋棪偼丄暘妱悢傪柍尷偲峫偊傞偲丂侾乛係乮偵尷傝側偔嬤偄抣乯偵側傞偲巚偄傑偡丅
偁偔傑偱丄梊應偺斖埻偱偡丅
夝摎丒偦偺2
乮儁儞僱亅儉丗偺偭偙傫乯
丂丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
侾乯俈摍暘揰傪偲傝丄堦斣嵍偺揰傪侾丄偦偺椬傝偺揰傪俀丄丒丒丒丄堦斣塃偺揰傪俇偲偡傞
嶰妏宍偑偱偒傞揰偺偲傝曽偼
丂丂侾偲係
丂丂俀偲係丄俀偲俆
丂丂俁偲係丄俁偲俆丄俁偲俇
慡晹偱侾亄俀亄俁亖俁丒係/俀丂捠傝
擟堄偺揰偺偲傝曽偼丂俇C俀亖俇丒俆/俀丂捠傝
妋棪偼俁丒係/俇丒俆
俀乯俉摍暘揰傪偲傝丄堦斣嵍偺揰傪侾丄丒丒丒丒丒丒丒丒丄堦斣塃偺揰傪俈偲偡傞
嶰妏宍偑偱偒傞揰偺偲傝曽偼
丂丂俀偲俆
丂丂俁偲俆丄俁偲俇
慡晹偱侾亄俀亖俁丒俀/俀丂捠傝
擟堄偺揰偺偲傝曽偼俈C俀亖俇丒俈/俀丂捠傝
妋棪偼俁丒俀/俇丒俈
俁乯俋摍暘揰傪偲傝丄丒丒丒丒丒丒丒丒
嶰妏宍偑偱偒傞揰偺偲傝曽偼
丂丂侾偲俆
丂丂俀偲俆丄俀偲俇
丂丂俁偲俆丄俁偲俇丄俁偲俈
丂丂係偲俆丄係偲俇丄係偲俈丄係偲俉
慡晹偱係丒俆/俀丂捠傝
擟堄偺揰偺偲傝曽偼俉C俀亖俉丒俈/俀丂捠傝
妋棪偼係丒俆/俉丒俈
係乯侾侽摍暘揰傪偲傝丄丒丒丒丒丒丒丒
嶰妏宍偑偱偒傞揰偺偲傝曽偼
丂丂俀偲俇
丂丂俁偲俇丄俁偲俈
丂丂係偲俇丄係偲俈丄係偲俉
慡晹偱係丒俁/俀丂捠傝
擟堄偺揰偺偲傝曽偼俋C俀亖俉丒俋/俀丂捠傝
妋棪偼係丒俁/俉丒俋
俆乯侾侾摍暘揰傪偲傝丄丒丒丒丒丒丒丒
嶰妏宍偑偱偒傞揰偺偲傝曽偼
丂丂侾偲俇
丂丂俀偲俇丄俀偲俈
丂丂俁偲俇丄俁偲俈丄俁偲俉
丂丂係偲俇丄係偲俈丄係偲俉丄係偲俋
丂丂俆偲俇丄俆偲俈丄俆偲俉丄俆偲俋丄俆偲侾侽
慡晹偱俆丒俇/俀丂捠傝
擟堄偺揰偺偲傝曽偼侾侽C俀亖侾侽丒俋/俀丂捠傝
妋棪偼俆丒俇/侾侽丒俋
俇乯侾俀摍暘揰傪偲傝丄丒丒丒丒丒丒丒
嶰妏宍偑偱偒傞揰偺偲傝曽偼
丂丂俀偲俈
丂丂俁偲俈丄俁偲俉
丂丂係偲俈丄係偲俉丄係偲俋
丂丂俆偲俈丆俆偲俉丆俆偲俋丆俆偲侾侽
慡晹偱俆丒係/俀丂捠傝
擟堄偺揰偺偲傝曽偼侾侾C俀亖侾侽丒侾侾/俀丂捠傝
妋棪偼俆丒係/侾侽丒侾侾
丂丂丂丂丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒丒
傑偲傔傞偲乮n亞2偲偡傞乯
(1)乮2n-1乯摍暘揰傪偲偭偨帪偺妋棪偼丂(n-1)n/(2n-2)(2n-3)亖(1/4)+乷3/(8n-12)乸
(2)丂2n摍暘揰傪偲偭偨帪偺妋棪偼丂(n-1)(n-2)/(2n-2)(2n-1)亖(1/4)-乷3/(8n-4)乸
丂丂丂丂丂丂丂丂丂丂丂丂仸偙偺曈偼徹柧偑昁梫偩偲巚偆偗傟偳傕丅
偄偢傟偵偣傛丄n傪廫暘偵戝偒偔偡傞偲妋棪偼丂侾/係丂偲側傞
夝摎丒偦偺3
乮儁儞僱亅儉丗偵偟傗傫乯
愗傝庢偭偨俁曈偺挿偝傪偦傟偧傟丄倎丄倐丄們 偲偡傞丅乮扨埵偼們倣乯
戣堄傛傝
丂丂丂倎亄倐亄們亖侾侽
奺曈偺挿偝偼惓側偺偱丄們傪徚嫀偟偰惍棟偡傞偲倎丄倐偺偲傝偆傞斖埻偼埲壓偲側傞丅
丂丂丂倎亜侽丄倐亜侽丄倎亄倐亙侾侽
偡側傢偪丄倎丆倐偺偲傝偆傞斖埻偼丄侾曈偑侾侽們倣偺捈妏擇摍曈嶰妏宍偺柺愊偵摍偟偄丅
丂丂丂侾侽仏侾侽乛俀亖俆侽
偙偺偆偪倎丆倐丆們偱嶰妏宍傪嶌傞偲偡傞偲丄俀曈偺榓偼丄巆傝侾曈傛傝傕戝偒偔側偗傟偽側傜側偄偺偱
丂丂丂倎亄倐亜們丄倐亄們亜倎丄們亄倎亜倐
忋婰傛傝丄們傪徚嫀偟偰惍棟偡傞偲
丂丂丂倎亙俆丄倐亙俆丄倎亄倐亜俆
偡側傢偪丄倎丆倐偺偲傝偆傞斖埻偼丄侾曈偑俆們倣偺捈妏擇摍曈嶰妏宍偺柺愊偵摍偟偄丅
丂丂丂俆仏俆乛俀亖侾俀丏俆
廬偭偰媮傔傞妋棪偼丄
丂丂丂侾俀丏俆乛俆侽亖侾乛係
夝摎丒偦偺4
乮儁儞僱亅儉丗Toru乯
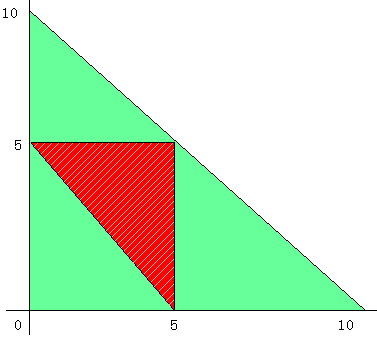
嵍抂偐傜x cm 塃抂偐傜y cm偱愗抐偡傞偲偡傞偲
丂丂丂x+y亙10,丂x亜0,丂y亜0
偙傟傪xy暯柺忋偵峫偊傞偲丄(0,0) (0,10) (10,0)傪寢傫偩嶰妏宍偺撪晹
偙偺椞堟偺偳偺揰傕摨偠妋棪偱婲偙傞偲峫偊傞丅
嶰妏宍偑偱偒傞忦審偼丄嶰曈偑丂x,丂y,丂10-x-y偩偐傜
丂丂丂x+y亜10-x-y,丂x+(10-x-y)亜y,丂y+(10-x-y)亜x傛傝
丂丂丂x+y亜5,丂x亙5,丂y亙5
偙傟偼(0,5) (5,5) (5,0)傪寢傫偩嶰妏宍偺撪晹偱丄
慜婰偺嶰妏宍偺奺曈偺拞揰傪寢傫偩嶰妏宍偲側偭偰偍傝丄柺愊偼侾乛係丅
傛偭偰嶰妏宍偺偱偒傞妋棪傕侾乛係
夝摎丒偦偺5
 乮儁儞僱亅儉丗忨偺偍偠偝傫乯
乮儁儞僱亅儉丗忨偺偍偠偝傫乯
妋棪偼丂侾乛係丂偱偡丅
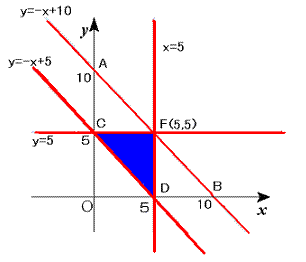
侾侽們倣恓嬥傪擟堄偺2揰偱愗抐偟傑偡丅偦偟偰嶰妏宍傪嶌傝傑偡偺偱師偺幃偑惉傝棫偪傑偡丅
擟堄偺揰偱愗抐偡傞偲堦曈傪俙們倣丄擇曈栚傪俛們倣丄偲偡傞偲嶰曈栚偼侾侽亅乮俙亄俛乯們倣偲側傝傑偡丅
嶰妏宍偼擇曈偺崌寁偼懠曈傛傝戝偒偄忦審偑偁傝傑偡丅
丂丂丂俙亄俛亜侾侽亅乮俙亄俛乯
丂丂丂俙亄乮侾侽亅乮俙亄俛乯乯亜俛丂仺丂侾侽亜俀B丂仺丂俆亜B
丂丂丂俛亄乮侾侽亅乮俙亄俛乯乯亜俙丂仺丂侾侽亜俀A丂仺丂俆亜A
丂丂丂俙亄俛亜俆丄俆亜俙亜侽丄俆亜俛亜侽
忋婰忦審偱師偺寁嶼傪偟傑偡丅
恓嬥偺愗抐億僀儞僩偼侾侽亊侾侽乛俀亖俆侽偱偡丅
嶰妏宍偵偡傞偨傔偺愗抐億僀儞僩偼俆亊俆乛俀亖侾俀丏俆偱偡丅
妋棪偼侾俀丏俆亐俆侽亖侽丏俀俆偲側傝摎偊偼侾乛係偱偡丅
夝摎丒偦偺6
乮儁儞僱亅儉丗teki乯
摎偊丂丂1/4
嶰妏宍偺惉棫忦審偼侾曈偺挿偝偑懠偺俀曈偺挿偝偺崌寁傛傝抁偄偙偲偱偡丅
偁偲偼丄偙傟傪晄摍幃偱偁傜傢偣偽丄僌儔僼傪昤偔偙偲偵傛偭偰丄捈妏擇摍曈
嶰妏宍偺柺愊斾偐傜弌偰偒傑偡丅乮側傫偲丄偙偙偵傕嶰妏宍偑搊応両乯
徻偟偄夝朄偼晄摍幃偲僌儔僼傪梡偄偰弤巕愭惗偛帺恎偑僐儘僉僂儉幒 NO.454
偵婰嵹偝傟偰傑偡偺偱丄徣棯偟傑偡丅
夝摎丒偦偺7
乮儁儞僱亅儉丗傒偗偹偙乯
朹傪丄倶丄倷丄侾侽亅倶亅倷丄偺俁杮偵愗抐偟偨偲偡傞丅
戣堄傛傝
丂丂丂侽亙倶亙侾侽丄侽亙倷亙侾侽丄侽亙侾侽亅倶亅倷乮亙侾侽乯
偑偄偊傞丅
偙傟傜偑帵偡椞堟偼壓恾偺乬椢乭乮奜懁偺嶰妏宍偺撪晹乯偱偁傞丅
傑偨丄嶰妏宍偑弌棃傞忦審偼丄
丂丂丂(1)丗倶亄倷亜侾侽亅倶亅倷
丂丂丂(2)丗倷亄侾侽亅倶亅倷亜倶
丂丂丂(3)丗侾侽亅倶亅倷亄倶亜倷
(1)丄(2)丄(3)傪惍棟偡傞偲丄
丂丂丂倷亜俆亅倶丄倶亙俆丄倷亙俆
偱偁傝丄偙傟傜偑帵偡椞堟偼壓恾偺乬愒乭乮撪懁偺嶰妏宍偺撪晹丄幬慄晹暘乯偱偁傞丅
慡帠徾偼忋恾偺乬椢乭乮奜懁偺嶰妏宍偺撪晹乯偺柺愊偱偁傝丄 嶰妏宍偑弌棃傞偺偼忋恾偺乬愒乭乮撪懁偺嶰妏宍偺撪晹丄幬慄晹暘乯 偺柺愊偱偁傞偐傜媮傔傞妋棪偼侾乛係偲側傞丅(廔)
夝摎丒偦偺8
乮儁儞僱亅儉丗傑乕傗乯
乮摎偊乯侾乛係
愗傝庢偭偨侾杮偺挿偝傪倶乮們倣乯丄傕偆侾杮傪倷乮們倣乯偲偡傞偲丄
巆傝偺侾杮偼丂10亅倶亅倷乮們倣乯偲側傞丅
恓嬥偺挿偝偼10們倣側偺偱丄
丂丂丂倶亄倷亙10丒丒丒乮侾乯
傑偨丄嶰妏宍偑偱偒傞偨傔偵偼丄
俁曈偡傋偰偵偍偄偰乽1曈偺挿偝亙懠偺2曈偺崌寁乿偑枮偨偝傟傟偽傛偄丅
傛偭偰丄
丂丂丂倶亙倷亄乮10亅倶亅倷乯丒丒丒乮俀乯
丂丂丂倷亙倶亄乮10亅倶亅倷乯丒丒丒乮俁乯
丂丂丂10亅倶亅倷亙倶亄倷丒丒丒乮係乯
丂丂丂乮俀乯傛傝丂倶亙俆丒丒丒乮俆乯
丂丂丂乮俁乯傛傝丂倷亙俆丒丒丒乮俇乯
丂丂丂乮係乯傛傝丂倶亄倷亜俆丒丒丒乮俈乯
乮侾乯丄乮俆乯丄乮俇乯丄乮俈乯偺斖埻傪恾帵偡傞偲丄
嶰妏宍偑偱偒傞妋棪偼丄僌儔僼偺仮AOB偵愯傔傞仮DFC偺柺愊偺妱崌側偺偱丄 侾乛係丂
夝摎丒偦偺9
乮儁儞僱亅儉丗岼偺柌乯
3杮偺恓嬥偺挿偝傪奺乆丄 偲偡傞偲丄恓嬥偺挿偝偑10噋偱偁傞偐傜丄
丂丂丂侽亙倎,倐丆們亙侾侽 丒丒丒(1)
偙偙偱嶰妏宍偑弌棃傞忦審傛傝丄
丂丂丂們亙倎亄倐
丂丂丂倐亙倎亄們丂丂丒丒丒(2)
丂丂丂倎亙倐亄們
偑惉棫偣偹偽側傜側偄丅 偙偙偱丄3曄悢傪2曄悢偵峣傝崬傓偲丄們亖侾侽亅倎亅倐丂偱偁傞偐傜丄
侽亙倎亄倐亙10丒丒丒(3)
偲側傞丅 偙傟傜(1)丄(2)媦傃(3)偺忦審偐傜
丂丂丂侽亙倎亙俆
丂丂丂侽亙倐亙俆丂丂丒丒丒(4)
丂丂丂俆亙倎亄倐
偑惉棫偡傞丅埲忋偺(1)乣(3)偺忦審壓偱(4)偺惉棫斖埻傪峫偊傞偲丄 惓偵偙傟偙偦嶰妏宍偑惉棫偡傞妋棪偱偁傞偐傜丄 偙傟傜傪嵗昗暯柺偵昞帵偡傞偲壓婰偺傛偆偵側傝丄
戝偒側嶰妏宍偺柺愊偵懳偟拞偺崟偄嶰妏宍晹暘偺柺愊斾偑媮傔傞傕偺偱偁傞丅 懄偪丄丂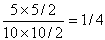
丂丂丂
夝摎丒偦偺10
乮儁儞僱亅儉丗抴鍋偺憙忛乯
恓嬥傪AB偲偟偰丄恾侾偺P,Q偑擟堄偺愗抐揰偱偡丅
偲偟傑偟傚偆丅戣堄傪姩埬偡傟偽
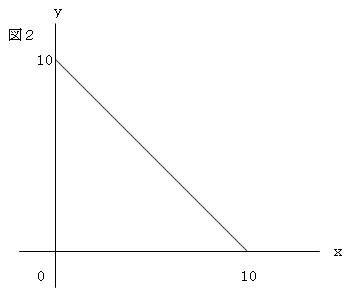
丂丂丂侽亙倶亙侾侽丂丂丂(1)
丂丂丂侽亙倷亙侾侽丂丂丂(2)
丂丂丂倶亄倷亙侾侽丂丂丂(3)
偱偡丅(1)(2)(3)傪摨帪偵枮偨偡忦審傪帇妎壔偟偰丄暯柺忋偵椞堟偲偟偰恾帵偡傞偲恾俀偺嶰妏抧懷偺撪晹偲側傝傑偡丅
愗抐偝傟偨俁杮偺恓嬥偱嶰妏宍偑惉棫偡傞忦審偼丄尵傢偢偲抦傟偨乽俀曈偺榓偼懠偺侾曈傛傝挿偄乿偱
丂丂丂俙俹亄俛俻亜俹俻丂丂丂(4)
丂丂丂俹俻亄俙俹亜俛俻丂丂丂(5)
丂丂丂俹俻亄俛俻亜俙俹丂丂丂(6)
(4)(5)(6)偑摨帪偵惉棫偡傞昁梫偑偁傝丄偐偮偦傟偱廫暘偱偡丅
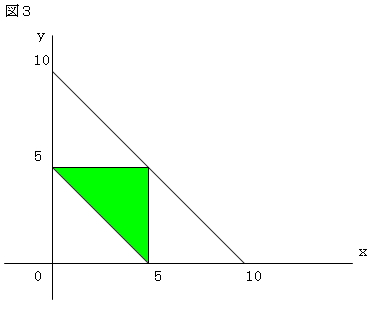
(4)(5)(6)傪椞堟偱昞帵偱偒傞傛偆偵偡傟偽
丂丂丂倶亄倷亜俆丂丂丂丂(7)
丂丂丂倷亙俆丂丂丂丂丂丂(8)
丂丂丂倶亙俆丂丂丂丂丂丂(9)
(7)(8)(9)傪摨帪偵枮偨偡椞堟傪恾俀偵廳偹偰恾帵偡傞偲恾俁傪摼傑偡丅怓偮偒偺椞堟偺撪晹偱偡丅慡懱偵愯傔傞柺愊偺妱崌偼25亾偱偡丅
廬偭偰丄愗抐偝傟偨俁杮偺恓嬥偱嶰妏宍傪嶌傞偙偲偑偱偒傞妋棪偼25亾偱偡丅
偲偙傠偱丄恀偺堄枴偱P,Q傪乽擟堄偺乿俀揰偲偡傞偙偲偼恖娫偺庤偱愗抐偡傞尷傝丄擄偟偄偺偱偼側偄偱偟傚偆偐丅 嵍塃偺僶儔儞僗姶妎偑摥偄偨傝偟偰丄恾俀偺嶰妏抧懷偺偡傋偰偺揰偑摍偟偄 奧慠惈傪傕偭偰婜懸偱偒傞偲偄偆偙偲偼偁傝摼側偄偱偟傚偆丅偦傟傪幚尰偱偒傞偺偼乽恄偺庤乿偲偄偆偙偲偱偟傚偆偐丅
夝摎丒偦偺11
乮儁儞僱亅儉丗俥倎倳倱俿乯
戣堄傛傝丄愗傝庢偭偨俁杮偺恓嬥偺挿偝傪丄
倶丄倷丄侾侽亅倶亅倷丂偲偡傟偽丄
丂丂丂侽亙倶亙侾侽丄丂侽亙倷亙侾侽亅倶
偑摼傜傟傞丅
傑偨丄嶰妏宍偑偱偒傞偨傔偺忦審偼丄
擟堄偺俀曈偺挿偝偺榓偑丄傕偆侾曈偺挿偝傛傝挿偔側傞偙偲偱偁傞偐傜丄
丂丂丂倶亄倷亜侾侽亅倶亅倷丂傛傝丂倷亜俆亅倶
丂丂丂倶亄乮侾侽亅倶亅倷乯亜倷丂傛傝丂倷亙俆
丂丂丂倷亄乮侾侽亅倶亅倷乯亜倶丂傛傝丂倶亙俆
偑摼傜傟傞丅
偙偙偱丄俁杮偵愗傝暘偗傞偩偗偺帠徾偼丄嶲峫恾偵偍偄偰丄
乮侽丆侽乯丆乮侾侽丆侽乯丆乮侽丆侾侽乯偺撪晹慡偰偱偁傝丄
偙偺偆偪丄俁杮偺恓嬥偑嶰妏宍傪側偡偨傔偺帠徾偼丄
乮俆丆侽乯丆乮俆丆俆乯丆乮侽丆俆乯偺撪晹慡偰偲側傞丅
亪丂媮傔傞妋棪偼丄柺愊斾傛傝
侾乛係丂偲側傞丅丂丒丒丒丒丒丒亂夝亃丂丂丂丂丂丂乮丂埲丂忋丂乯
夝摎丒偦偺12
乮儁儞僱亅儉丗嶰妏掕婯乯
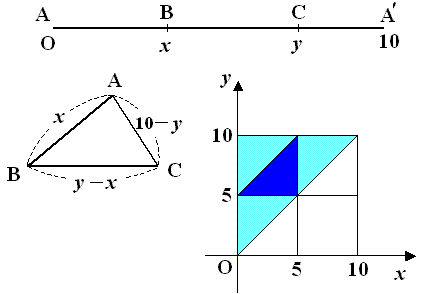
恾偺傛偆偵丆挿偝10偺慄暘 AA' 傪俀揰B丆C偱愜傝嬋偘嶰妏宍傪嶌傞偙偲傪峫偊傞丅
AB亖x丆AC亖y 偲偡傞偲丂0亙x亙y亙10 乧(1)丂偱偁傝丆俁曈偑嶰妏宍傪嶌傞偺偼丆
丂丂丂AB亙BC亄CA 傛傝丆x亙10亅x丂丂亪 x亙5 乧(2)
丂丂丂CA亙AB亄BC 傛傝丆10亅y亙y丂丂亪 y亜5 乧(3)
丂丂丂BC亙CA亄AB 傛傝丆y亅x亙10亅y亄x丂亪 y亙x亄5 乧(4)
丂
(1)偼恾偺悈怓晹暘乮柺愊50乯偱丆(2)(3)(4)偼惵怓晹暘乮柺愊25/2)偱偁傞丅
傛偭偰丆嶰妏宍偲側傞妋棪偼丆(25/2)/50亖1/4丂乵摎乶
僄僋僙儖偱僔儈儏儗乕僔儑儞傪偟偰傒偨傜丆22/100丆48/200丆96/400丆197/800 偲奣偹 1/4 偵側傝傑偟偨丅
夝摎丒偦偺13
乮儁儞僱亅儉丗揮埵斀墳乯
侾侽噋偺恓嬥傪擟堄偺擇揰偱愗抐偟偰偱偒傞嶰杮偺恓嬥偺挿偝傪
倎丆倐丆們偲偡傞偲丄
丂丂丂侽亙倎亙侾侽丆丂侽亙倐亙侾侽丆丂侽亙們亙侾侽
偱偁傞丅丂
傑偨丄倎亄倐亄們亖侾侽丂側偺偱
丂丂丂倎亄倐亖侾侽亅們丂亙侾侽
廬偭偰丄曄悢倎丆倐偵偮偄偰惍棟偡傞偲
丂丂丂侽亙倎亙侾侽丆丂侽亙倐亙侾侽丆丂侽亙倎亄倐亙侾侽丂
倎丆倐傪嵗昗幉偵偲偭偰僌儔僼偵帵偡偲丄壓婰偺捠傝丅
偮傑傝丄恓嬥偺愗抐偵傛傝丄婲偙傝偆傞慡偰偺倎丆倐偺慻崌偣偼丄
(侽丆侽)丄丂(侽丆侾侽)丄丂(侾侽丆侽)丂傪捀揰偲偡傞捈妏擇摍曈嶰妏宍偺
撪懁偺揰偱偁傞丅扐偟丄嫬奅慄忋偺揰偼娷傑側偄丅
堦曽丄偙傟傜嶰杮偺恓嬥偱嶰妏宍偑惉棫偡傞昁梫廫暘忦審偼丄
丂丂丂倎亄倐亜們丆丂倐亄們亜倎丆丂們亄倎亜倐
傪慡偰枮偨偡偙偲偱偁傞丅
們亖侾侽亅倎亅倐丂傪梡偄偰丄倎丆倐偵偮偄偰惍棟偡傞偲
丂丂丂侽亙倎亙俆丆丂侽亙倐亙俆丆丂俆亙倎亄倐亙侾侽
偙傟傜偺忦審傪摨帪偵枮偨偡慡偰偺倎丆倐偺慻崌偣偼丄
(俆丆侽)丂(侽丆俆)丂(俆丆俆)傪捀揰偲偡傞捈妏擇摍曈嶰妏宍偺撪懁偺
揰偱偁傞丅扐偟丄嫬奅慄忋偺揰偼娷傑側偄丅
埲忋偺寢壥偐傜丄婲偙傝偆傞慡偰偺揰(倎丆倐)偺慻崌偣偵懳偟偰丄
嶰妏宍偑惉棫偡傞応崌偺揰(倎丆倐)偺慻崌偣偺悢偺妱崌偼丄
忋婰擇偮偺捈妏擇摍曈嶰妏宍偺柺愊斾偵摍偟偄偙偲偵側傞丅
偙傟傜偺捈妏擇摍曈嶰妏宍偺憡帡斾偼侾丗俀偱偁傞偙偲偐傜丄
柺愊斾偼侾丗係偱偁傞丅傛偭偰丄戣堄偺妋棪偼侾乛係偲側傞丅
夝摎丒偦偺14
乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫乯
摎偊偼丄侾乛係偱偡丅
嶰妏宍偺俁曈偵偼丄師偺娭學偑偁傝傑偡丅
丂乮偁乯偳偺俀曈偺榓傕懠偺侾曈傛傝挿偄
丂乮偄乯偳偺俀曈偺嵎傕懠偺侾曈傛傝抁偄
幚偼乮偁乯偲乮偄乯偼摨偠偙偲偱偡丅
嶰妏宍偺挿偝傪俁曈傪倎丄倐丄們偲偟傑偡丅
丂倎亄倐亜們丂丒丒丒丂乮侾乯
丂倐亄們亜倎丂丒丒丒丂乮俀乯
丂們亄倎亜倐丂丒丒丒丂乮俁乯
乮侾乯偐傜倐乮倎乯傪塃曈偵堏崁偡傞偲丄倎亜們亅倐乮倐亜們亅倎乯
乮俀乯偐傜們乮倐乯傪塃曈偵堏崁偡傞偲丄倐亜倎亅們乮們亜倎亅倐乯
乮俁乯偐傜倎乮們乯傪塃曈偵堏崁偡傞偲丄們亜倐亅倎乮倎亜倐亅們乯
倎丄倐丄們偺戝彫偵娭學側偔偙偺俇偮偺幃傪暪偣傟偽乮偄乯偑偄偊傑偡丅
偩偐傜乮偁乯偺忦審偩偗傪峫偊傑偡丅
恓嬥偵偲傞俀揰傪倃丄倄偲偟傑偡丅乮嵍偺揰傪倃偲偟傑偡乯
嵍抂偐傜偺揰倃丄倄傑偱偺嫍棧傪倶丄倷偲偟傑偡丅
偡傞偲恓嬥偺挿偝偼丄乮倎乯倶丄乮倐乯倷亅倶丄乮們乯侾侽亅倷偲側傝傑偡丅
仠恾侾
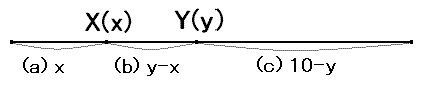
侾曈偑侾侽偺惓曽宍偺拞偵丄嵍偐傜倶偺偲偙傠丄壓偐傜倷偺偲偙傠偵揰傪偲傝傑偡丅
嵍偺揰傪倃偲偟偰偄傞偺偱丄倷亜倶乮恾偺嵍忋乯偺晹暘偺榖偱偡偑丄塃偵倃偑偔傞応崌偼丄
倷亖倶偵娭偟偰懳徧側晹暘偵側傝傑偡丅
仠恾俀
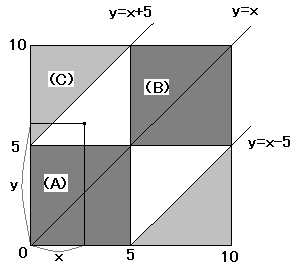
嶰妏宍偑偱偒傞応崌傪峫偊傞偲丄乮倶丆倷乯偼
丂乮俙乯嵍壓偺晹暘偵偼偁傝傑偣傫乮們偑俆們倣傛傝挿偄偺偱乯
丂乮俛乯塃忋偺晹暘偵偼偁傝傑偣傫乮倎偑俆們倣傛傝挿偄偺偱乯
丂乮俠乯嵍忋偺晹暘偵偼偁傝傑偣傫乮倐偑俆們倣傛傝挿偄偺偱乯
媡偵巆偭偨晹暘偵乮倶丆倷乯偑偁傟偽丄偳偺俀曈偺榓傕懠偺侾曈傛傝挿偔側偭偰偄傑偡丅
仠恾俁
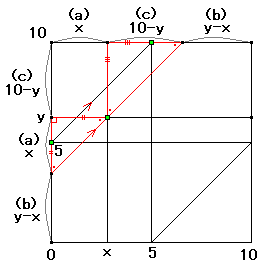
恾偺嵍偺曈偱丄
丂丂丂倎亄倐亜俆亜們傛傝丄倎亄倐亜們丂丒丒丒丂乮侾乯
丂丂丂們亄倎亜俆亜倐傛傝丄們亄倎亜倐丂丒丒丒丂乮俁乯
恾偺忋偺曈偱丄
丂丂丂倐亄們亜俆亜倎傛傝丄倐亄們亜倎丂丒丒丒丂乮俀乯
偲側傝傑偡丅
偙偺侾曈侾侽偺惓曽宍偺拞偺揰偑偳傟傕摨偠傛偆偱嬫暿偑側偄偲偡傞偲媮傔傞妋棪偼柺愊偺斾偵側傝傑偡丅
亂偍傑偗亃
偳偺曈傕俆們倣傛傝傕抁偗傟偽嶰妏宍偑偱偒傑偡丅
嵟弶偵庢偭偨揰傪X乮敿暘傛傝嵍乯偲偟傑偡丅
嶰妏宍偑偱偒傞偨傔偵偼丄倄偼倃偐傜傕塃抂偐傜傕俆們倣埲撪偵偁傟偽傛偄偙偲偵側傝傑偡丅
仠恾係
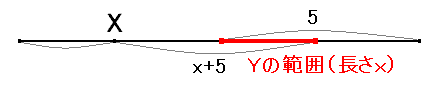
倶偺抣偵懳偟偰倄傪偲偭偨偲偒偵嶰妏宍偑偱偒傞妋棪
乮倄偺斖埻偺挿偝乛侾侽乯傪僌儔僼偵偡傞偲師偺傛偆偵側傝傑偡丅
仠恾俆
惓夝幰
| teki | 傒偗偹偙 | 揮埵斀墳 |
| 栭傆偐偟偺偮傜偄偍偠偝傫 | 傑偡傑偡僞僐偝傫 | 傑乕傗 |
| Toru | 偺偭偙傫 | 忨偺偍偠偝傫 |
| 岼偺柌 | 偵偟傗傫 | 嶰妏掕婯 |
| 抴鍋偺憙忛 | 俥倎倳倱俿 |
傑偲傔
枅寧偺栤戣傕丄偙傟偱NO.120偱偡偐傜丄侾侽擭偲偄偆偙偲偵側傝傑偡丅
挿偔偍偮偒崌偄偄偨偩偄偰偄傞奆偝傫偵怱偐傜姶幱怽偟忋偘傑偡丅
堷偒懕偒丄偙傟偐傜傕偳偆偧傛傠偟偔偍婅偄偄偨偟傑偡丅
偝偰丄崱夞偺栤戣偱偡偑丄幚偼偙偺僥乕儅偼丄teki偝傫偺偛巜揈偵傕偁傞傛偆偵丄
埲慜丄僐儘僉僂儉幒偱庢傝忋偘偨偙偲偑偁傝傑偟偨丅
妋棪偼丄偡傋偰偺帠徾偺屄悢偲丄忦審偵崌偆帠徾偺屄悢偱斾傪偲偭偰丄
媮傔傑偡偑丄偙偺栤戣偵傛偆偵楢懕揑偵曄壔偡傞応崌偼丄侾屄丄俀屄偲
屄悢偱悢偊傜傟傑偣傫丅
侾師尦側傜挿偝偺斾丄俀師尦側傜柺愊偺斾偱媮傔傞偙偲偵側傝傑偡丅
偦偙偑丄偙偺栤戣偺偍傕偟傠偄偲偙傠偐側偲巚偄傑偡丅
傑偡傑偡僞僐偝傫丄偺偭偙傫偝傫偺
夝摎偼丄暘妱傪柍尷偵偟偰偄偭偰丄偦偺嬌尷抣偲偟偰丄
妋棪傪掕媊偯偗傞偲偄偆偍傕偟傠偄夝朄偱偡偹丅
旝暘偺峫偊曽偵捠偠傞傕偺偑偁傝丄姶怱偄偨偟傑偟偨丅
 top
top