円(半径の長さ1)の内接正N角形と外接正N角形を考えると、それぞれの周の長さに以下のような不等式が成り立ちます。
内接正N角形の周の長さ<円周の長さ<外接正N角形の周の長さ
半径1の円周の長さは、2πですから、
内接正N角形の周の長さ<2π<外接正N角形の周の長さ
従って、内接正N角形と外接正N角形の周の長さを求めることができれば、 円周率πの値を近似できるということになります。
Nの値を大きくとることで、精度をあげることができます。
では、内接正N角形と外接正N角形の周の長さはどのようにして求めればいいでしょうか?
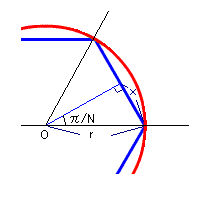
* 内接正N角形の周の長さ *
左の図の直角三角形に注目してください。
x/r = sin(π/N)より、x = r・sin(π/N)
が成り立ちます。従って、
内接正N角形の周の長さ=2Nx=2Nr・sin(π/N)
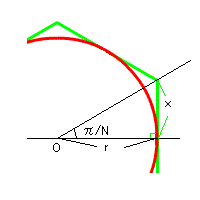
* 外接正N角形の周の長さ *
左の図の直角三角形に注目してください。
x/r = tan(π/N)より、x = r・tan(π/N)
が成り立ちます。従って、
外接正N角形の周の長さ=2Nx=2Nr・tan(π/N)
 戻る
戻る