Weekend Mathematics/コロキウム室/テーマ別
/9.長方形の問題
コロキウム室(長方形の問題)
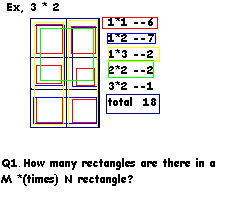
NO.194 11/8 Mami 長方形の問題(1)
Kon nichi wa!!
watashi wa "venezuela"(nannbei no kuni) ni sun deiru 16 no girl desu.
gakkou ( international school) de tugi no youna mondai wo raishuu no
kayoubi made ni yarinasai to iwareta nodesuga, dou yatte yaru no kaga
wakarimasen. nanode tasukete kudasai.
shitumon wa tugi ni kaitearumonodesu.
"How many rectangle are there in a M times N rectangle?"
M kakeru N no chouhokei niwa ikutu no chouhoukei ga arimasuka?
こんにちは。
私はベネズエラ(南米の国)に住んでいる16才の女の子です。
学校で次のような問題を来週の火曜日までにやりなさいといわれたのですが、
どうやってやるのかわかりません。なので、助けてください。
質問は次にかいてあるものです。
「M×Nの長方形にはいくつの長方形がありますか?」

NO.195 11/9 Junko 長方形の問題(2)

まず2×3の長方形で考えてみます。
例示されているように、正方形も含んで考えます。
(正方形は長方形の特殊な場合と考えます。)
含まれる長方形をサイズ別に考えるのではなく、
縦のサイズと横のサイズの組み合わせとして考えていきます。
まず、縦です。サイズ1とすると3通り。
サイズ2が、2通り。
そして、サイズ3が1通りですから、合わせて6通り。
横です。サイズ1とすると、2通り。
サイズ2とすると1通りですから、合わせて3通り。
長方形は、縦と横の組み合わせでできますから、6×3=18通りとなります。
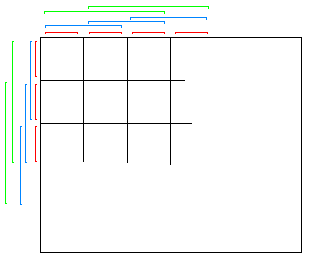
さて、次は一般にM×Nの場合ですが同じようにできます。
まず、縦です。サイズ1とするとM通り。
サイズ2とすると(M−1)通り。
サイズ3とすると(M−2)通り。
・・・と同様にいきまして、最後にサイズMが1通りとなります。
それらをすべて足せばいいわけですから、
M+(M−1)+(M−2)+・・・+2+1=(1/2)M(M+1)通り。
次に横ですが、同じようにできますから、
N+(N−1)+(N−2)+・・・+2+1=(1/2)N(N+1)通り。
従って、長方形の総数は、
(1/2)M(M+1)×(1/2)N(N+1)=(1/4)M(M+1)N(N+1)となります。

NO.196 11/9 水の流れ 長方形の問題(3)
M×Nの長方形を縦線(N+1)本 、
横線(M+1)本で表すことにします。
長方形は縦線2本と横線2本から、1個の長方形が作れます。
だから、
縦線N+1本から、2本とる方法はN+1C2
横線N+1本から、2本とる方法はM+1C2
したがって、
N+1C2×M+1C2
=N(N+1)/2×M(M+1)/2
=MN(M+1)(N+1)/4・・・(答え)
そこで、Venezuela の先生に問題です。
このM×Nの長方形(M≧Nとする)の中に正方形は
一体いくつありますか?
”How many right angle are
there in a M times N rectanngle?”

NO.198 11/10 水の流れ 長方形の問題(4)
「2×1の長方形を隙間なく敷き詰めて、2×nの長方形を作る
方法は何通りあるでしょう?」
ヒント:やはり、n=1,2,3,4,・・・、と、実際に作ってみてください。
規則性が分かってきます。
(問題の訂正11/11、20:00)

NO.200 11/13 Junko 長方形の問題(5)
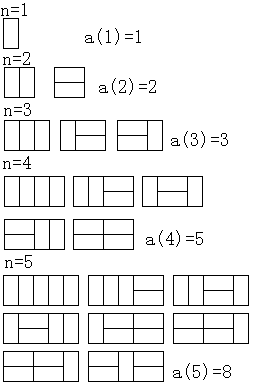
試しにやってみました。
2×nの長方形に2×1の長方形を敷き詰める方法の
数をa(n)と表すことにします。
左の図のように、
a(1)=1、a(2)=2、a(3)=3、a(4)=5、a(5)=8、・・・となります。
あれ−っ! これってフィボナッチ数列?
フィボナッチ数列というのは、F0=1、F1=1、
Fn-2+Fn-1=Fn(n≧2)
で定義される数列です。
これに従って、いくつか求めてみましょう。
F2=2、F3=3、F4=5、F5=8、
F6=13、F7=21、F8=34、F9=55、
F10=89、F11=144、F12=233、・・・
フィボナッチ数列の始まりは「うさぎの問題」だといわれています。
つまり、「生まれたばかりの1つがいのうさぎは
2ヶ月目から毎月1つがいのうさぎを産むとする。
すべてのうさぎがこの規則にしたがい、死ぬことはないとするとき、
1つがいのうさぎは1年後に何つがいのうさぎになるか。」というものです。
また、フィボナッチ数は黄金比と密接な関係がありますし、おもしろい性質がたくさんあります。
そして、フィボナッチ数列の一般項もわかっています。
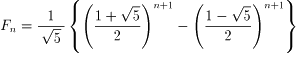
フイボナッチ数について、詳しく知りたい方は、講談社のブル−バックスにある
佐藤修一著「自然にひそむ数学」という本がおすすめです。
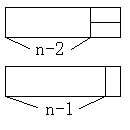 今回の問題の場合もこう考えれば、フィボナッチ数列であることがわかります。
今回の問題の場合もこう考えれば、フィボナッチ数列であることがわかります。
2×nの長方形の敷き詰め方は、左の図のような2種類に分類されます。
1つは、左から(n-2)個敷き詰めた(敷き詰め方はa(n-2)通り)後、
横向きに2つ敷き詰めます。
もう1つは、左から(n-1)個敷き詰めた(敷き詰め方はa(n-1)通り)後、
縦に1つ敷きます。
従って、a(n)=a(n-2)+a(n-1)が成り立ちます。
これはフィボナッチ数列に他なりません。

NO.202 11/15 Junko 長方形の問題(6)
「N段ある階段を1段ないし、2段づつ登るとき、
その登り方の総数Fnはいくつでしょう?」
この問題の答えもフィボナッチ数列です。
N段ある階段の最後の段階を考えます。
(N−2)段目から、最後2段進んで登り切るか、
(N−1)段目から、最後1段進んで終わるかのいずれかになります。
従って、Sn=Sn−2+Sn−1
という漸化式がなりたちます。
S1=1、S2=2ですから、
フィボナッチ数列に他なりません。
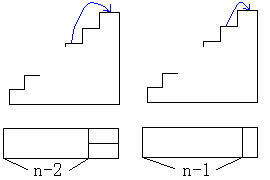
これを、前回の長方形の敷き詰め問題に対応させて考えることもできます。
左の図のように最後の段階で、階段を2段登るというのは、
長方形を横に2つ並べることに対応させます。
また階段を1段登るということは長方形を縦に置くことに対応させればいいわけです。

NO.204 11/18 海津北高校情報処理科2年 長方形の問題(7)
数学の時間に考えた問題の解答を送ります。
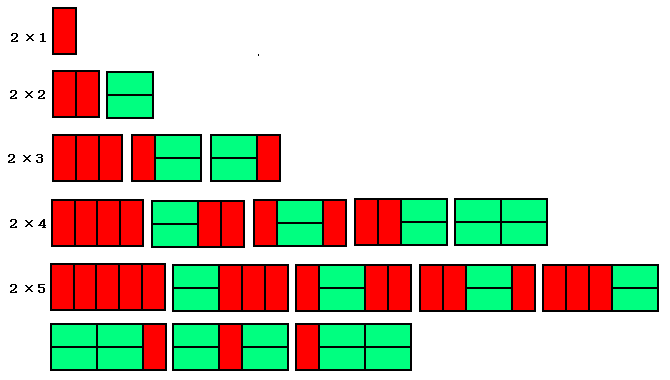
2×1・・・1
2×2・・・2
2×3・・・3
2×4・・・5
2×5・・・8
・・・
となっているので、2×n(n>2)の長方形の場合は
2×(n−1)の場合の答えと2×(n−2)の場合の答えを
合計したものになります。
このような数列をフィボナッチ数列と呼ぶそうです。
身近なものにこのような数列が隠されていて
とても驚きました。

NO.230 12/14 水の流れ 長方形の問題(8)
NO.196で、提起した問題です。
このM×Nの長方形(M≧Nとする)の中に正方形は
一体いくつありますか?
”How many right angle are
there in a M times N rectanngle?”
最初は順に数えてみましょう。
- 1×1の正方形・・・M×N
- 2×2の正方形・・・(M-1)(N-1)=MN-(M+N)+12
- 3×3の正方形・・・(M-2)(N-2)=MN-2(M+N)+22
- 4×4の正方形・・・(M-3)(N-3)=MN-3(M+N)+32
- 5×5の正方形・・・(M-4)(N-4)=MN-4(M+N)+42
- ・・・
- N×Nの正方形・・・(M-N+1)(N-N+1)=MN−(N-1)(M+N)+(N-1)2
以上を、全部足して
注:
1+2+3+・・・+n=n(n+1)/2
12+22+32+・・・+n2=n(n+1)(2n+1)/6
となる公式は知っていますか?
これを利用します。
求める正方形の個数は
N×MN-{1+2+3+・・・+(N-1)}(M+N)+{12+22+32+・・・+(N-1)2}
=N(N+1)(3M-N+1)/6 (答)
また、M=Nのとき、2乗の公式
12+22+32+・・・+n2=
n(n+1)(2n+1)/6
になっています。

 戻る
戻る





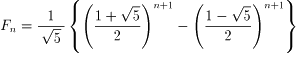
 今回の問題の場合もこう考えれば、フィボナッチ数列であることがわかります。
今回の問題の場合もこう考えれば、フィボナッチ数列であることがわかります。



 戻る
戻る