Weekend Mathematics�^�R���L�E�����^�e�[�}���^29.�O�p�`�̖ʐ�
| NO.618 | '99 10/3 | ���̗��� | �O�p�`�̖ʐρi�P�j |

�����̖�������āA���e���ł��B
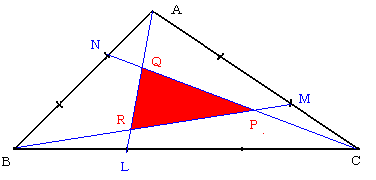
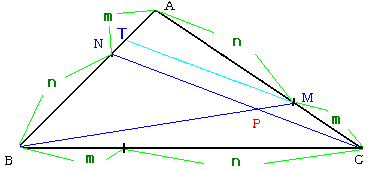
�O�p�`�`�a�b�̊e�ӂa�b�A�b�`�A�`�a���P�F�Q�ɓ��������_�����ꂼ��k�A�l�A
�m�@�Ƃ��܂��B
�a�l�Ƃb�m�A�b�m�Ƃ`�k�C�`�k�Ƃa�l�̌�_�����ꂼ��o�A�p�A�q�Ƃ��܂��B
�O�p�`�`�a�b�̖ʐς͎O�p�`�o�p�q�̖ʐς̉��{�ł��傤���B
�܂��A��ʂɁA�������̂Ƃ��A�e�ӂ����F���ɓ��������_���k�A�l�A�m�Ƃ�
�āA���l�ɁA�l���Ă݂Ă��������B

| NO.619 | '99 10/7 | Junko | �O�p�`�̖ʐρi�Q�j |
�_�q�͐����a�l��̓_�ł�����A�����`�k��̓_�ł�����̂ŁA
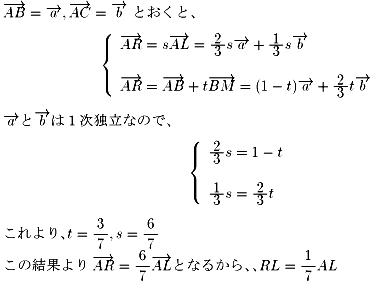
���`�a�b�̖ʐς��r�Ƃ���ƁA
���`�a�k�����a�b�l�����b�`�m��(1/3)�r
�Ώ̐��Ɛ�قǂ̌��ʂ���A
���a�k�q�����b�l�o�����`�m�p��(1/3)�(1/7)�r��(1/21)�r
| ���o�p�q | ���r�|(���`�a�k�{���a�b�l�{���b�`�m)�{(���a�k�q�{���b�l�o�{���`�m�p) |
| ���r�|(1/3)�r��R�{�i1/21)�r��R | |
| ��(1/7)�r |
�����@�@�@�@�V�{

| NO.621 | '99 10/9 | Junko | �O�p�`�̖ʐρi�R�j |
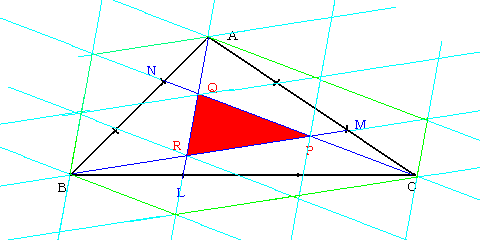
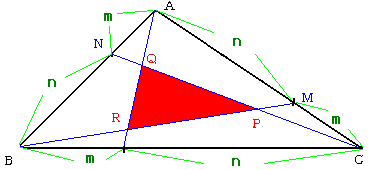
���o�p�q�̎O�ӂɕ��s�Ȓ������Ђ��Ă݂܂����B
���ΐF�ň͂܂ꂽ�Z�p�`�̕����́A���o�p�q�̖ʐς̂��傤�ǂP�R�{�ɂȂ��Ă��܂��B
�i�����Ă݂Ă��������B�j
�܂��ʂȌ�����������`�a�b���灢�o�p�q�������������̂Q�{�{���o�p�q�ƂȂ��Ă��܂��B
���̂��Ƃ���A�V�{�ƌ��_�Â��邱�Ƃ��ł��܂��B

| NO.622 | '99 10/12 | �l�c�@���� | �O�p�`�̖ʐρi�S�j |
Visual Basic�ʼnv���O����������Ă݂܂����D
�v���O�����̓��e�͈ȉ��̒ʂ�ł��D
�������g���R�_�`�C�a�C�b�̍��W�����肵�C�_�k�C�l�C�m�C�o�C�p�C�q�̍��W�����߁C
�w�����̌������g���C���`�a�b�C���o�p�q�̖ʐς��v�Z���C
�䁢�`�a�b�^���o�p�q���v�Z����D
���̎��s���T�O�O��ishikoukaisuu�j�J��Ԃ��C���ꂼ��̏ꍇ�̖ʐϔ���v�Z���C
�ʐϔ�̕��ς����߂�D
���̃v���O�����ɂ��C���͂V�ɂȂ鎖��������܂��D
�v���O�����͂Q����C�P�ڂ͔�ir�j���P�^�R�̏ꍇ�ŁC���ꂼ��̎O�p�`��}�����܂��D
�Q�ڂ͔�ir�j���O�ƂO.�T�̊Ԃ̏ꍇ�ŁC�O���t�ŕ`�ʂ��Ă��܂��D
�܂��f�[�^���t�@�C���ɗ��Ƃ��悤�ɂȂ��Ă��܂�
�O���t�͐Ԃ��`�����̂ł����C�\����ˑR�����Ȃ�܂��D
����͂�(��)��(�P�|���{��2)�^(�P�|�Q��)2�̃O���t���㏑������ׂł��D
����ɂ��C
����(�P�|���{��2)�^(�P�|�Q��)2��(��2�{�����{��2)�^(���|��)2�ł��鎖��������܂��D
�䂪�P�^�R�̏ꍇ
Option Explicit
Const r = 1 / 3
Sub Form_Load()
Picture1.Scale (-1, -1)-(1, 1)
End Sub
Sub Command1_Click()
'�O�p�`�̖��2
Randomize Timer
Dim j1, j2, j3, j4, j, jj, jjj, iro0, iro1, iro2, dame As Integer
iro0 = RGB(0, 0, 255): iro1 = RGB(255, 255, 0)
iro2 = RGB(0, 0, 0)
Dim shikoukaisuu, kaisuu, machijikan As Long
shikoukaisuu = 500: kaisuu = 0: machijikan = 400000
Dim x(1, 8), d(1, 2), a(2), b(2), c(2), bumbo, hen(2), s As Double
Dim menseki(1), wa, hi, d_genkai, hi_genkai As Double
wa = 0: d_genkai = 0.01: hi_genkai = 10 ^ (-12)
Dim ten(8) As String
ten(0) = "A": ten(1) = "B": ten(2) = "C"
ten(3) = "L": ten(4) = "M": ten(5) = "N"
ten(6) = "R": ten(7) = "P": ten(8) = "Q"
Picture3.Cls: Picture4.Cls
For j1 = 0 To shikoukaisuu
For j2 = 0 To 2
For j3 = 0 To 1
If j1 = 0 Then
x(j3, j2) = Rnd * 2 - 1: d(j3, j2) = (Rnd * 2 - 1) * d_genkai
Else
d(j3, j2) = d(j3, j2) + (Rnd * 2 - 1) * d_genkai
If Abs(d(j3, j2)) > d_genkai Then
d(j3, j2) = -Sgn(d(j3, j2)) * d_genkai
End If
x(j3, j2) = x(j3, j2) + d(j3, j2)
If Abs(x(j3, j2)) > 1 Then x(j3, j2) = Sgn(x(j3, j2))
End If
Next
Next
For j2 = 0 To 2
j = (j2 + 1) Mod 3: jj = (j + 1) Mod 3: jjj = j2 + 3
For j3 = 0 To 1
x(j3, jjj) = (1 - r) * x(j3, j) + r * x(j3, jj)
Next
a(j2) = x(1, jjj) - x(1, j2): b(j2) = x(0, j2) - x(0, jjj)
c(j2) = x(0, j2) * x(1, jjj) - x(0, jjj) * x(1, j2)
Next
dame = 0
For j2 = 0 To 2
If dame = 0 Then
j = (j2 + 1) Mod 3: jj = j2 + 6
bumbo = a(j2) * b(j) - b(j2) * a(j)
If bumbo = 0 Then
dame = 1
Else
x(0, jj) = (b(j) * c(j2) - b(j2) * c(j)) / bumbo
x(1, jj) = (a(j2) * c(j) - a(j) * c(j2)) / bumbo
End If
End If
Next
If dame = 0 Then
For j2 = 0 To 1: s = 0
For j3 = 0 To 2
j = j3 + j2 * 6: jj = ((j3 + 1) Mod 3) + j2 * 6: hen(j3) = 0
For j4 = 0 To 1
hen(j3) = hen(j3) + (x(j4, j) - x(j4, jj)) * (x(j4, j) - x(j4, jj))
Next
hen(j3) = Sqr(hen(j3)): s = s + hen(j3)
Next
s = s * 0.5: menseki(j2) = s
For j3 = 0 To 2
menseki(j2) = menseki(j2) * (s - hen(j3))
Next
Next
End If
Picture1.Cls
Picture1.PSet (x(0, 0), x(1, 0)), iro0
For j2 = 2 To 0 Step -1
Picture1.Line -(x(0, j2), x(1, j2)), iro0
Next
For j2 = 0 To 2: j = j2 + 3
Picture1.Line (x(0, j2), x(1, j2))-(x(0, j), x(1, j)), iro1
Next
If dame = 0 Then
Picture1.PSet (x(0, 6), x(1, 6)), iro2
For j2 = 8 To 6 Step -1
Picture1.Line -(x(0, j2), x(1, j2)), iro2
Next
End If
For j2 = 0 To 8 - dame * 3
Picture1.CurrentX = x(0, j2): Picture1.CurrentY = x(1, j2)
Picture1.Print ten(j2)
Next
Picture2.Cls: Picture2.Print j1; "�s"
If menseki(1) >= hi_genkai Then
For j2 = 0 To 1: menseki(j2) = Sqr(menseki(j2)): Next
hi = menseki(0) / menseki(1): wa = wa + hi: kaisuu = kaisuu + 1
Picture3.Cls: Picture3.Print "��ABC/��PQR="; hi
Picture4.Cls: Picture4.Print "���� ="; wa / kaisuu
End If
For j2 = 0 To machijikan: Next
Next
Beep
End Sub
Private Sub Command2_Click()
End
End Sub
�䂪���^(���{��)�̏ꍇ
Option Explicit
Sub Form_Load()
Picture1.Scale (-1, -40)-(1, 40)
End Sub
Sub Command1_Click()
'�O�p�`�̖��3
Randomize Timer
Dim j1, j2, j3, j4, j, jj, jjj, iro0, iro1, iro2, dame As Integer
iro0 = RGB(0, 0, 0): iro1 = RGB(255, 0, 0): iro2 = RGB(255, 255, 255)
Dim shikoukaisuu, kaisuu As Long
shikoukaisuu = 500
Dim x(1, 8), y, a(2), b(2), c(2), bumbo, hen(2), s As Double
Dim r, menseki(1), wa, hi, hi_genkai, kizami As Double
hi_genkai = 10 ^ (-12): kizami = 0.01
Picture1.Cls: Picture2.Cls: Picture3.Cls
For j1 = -36 To 36 Step 4
Picture1.Line (-1, j1)-(1, j1), iro2
Next
For j1 = -9 To 9
Picture1.Line (0.1 * j1, -40)-(0.1 * j1, 40), iro2
Next
Picture1.Line (-1, 0)-(1, 0), iro0
Picture1.Line (0, -40)-(0, 40), iro0
Picture4.Cls: Picture4.Print "����0.1�����݁C�c��4������"
Open "sankaku3.dat" For Output As #1
For r = 0 To 0.5 - kizami Step kizami
wa = 0: kaisuu = 0
For j1 = 1 To shikoukaisuu
For j2 = 0 To 2: For j3 = 0 To 1: x(j3, j2) = Rnd: Next: Next
For j2 = 0 To 2
j = (j2 + 1) Mod 3: jj = (j + 1) Mod 3: jjj = j2 + 3
For j3 = 0 To 1
x(j3, jjj) = (1 - r) * x(j3, j) + r * x(j3, jj)
Next
a(j2) = x(1, jjj) - x(1, j2): b(j2) = x(0, j2) - x(0, jjj)
c(j2) = x(0, j2) * x(1, jjj) - x(0, jjj) * x(1, j2)
Next
dame = 0
For j2 = 0 To 2
If dame = 0 Then
j = (j2 + 1) Mod 3: jj = j2 + 6
bumbo = a(j2) * b(j) - b(j2) * a(j)
If bumbo = 0 Then
dame = 1
Else
x(0, jj) = (b(j) * c(j2) - b(j2) * c(j)) / bumbo
x(1, jj) = (a(j2) * c(j) - a(j) * c(j2)) / bumbo
End If
End If
Next
If dame = 0 Then
For j2 = 0 To 1: s = 0
For j3 = 0 To 2
j = j3 + j2 * 6: jj = ((j3 + 1) Mod 3) + j2 * 6: hen(j3) = 0
For j4 = 0 To 1
hen(j3) = hen(j3) + (x(j4, j) - x(j4, jj)) * (x(j4, j) - x(j4, jj))
Next
hen(j3) = Sqr(hen(j3)): s = s + hen(j3)
Next
s = s * 0.5: menseki(j2) = s
For j3 = 0 To 2
menseki(j2) = menseki(j2) * (s - hen(j3))
Next
Next
If menseki(0) >= hi_genkai And menseki(1) >= hi_genkai Then
For j2 = 0 To 1: menseki(j2) = Sqr(menseki(j2)): Next
wa = wa + menseki(0) / menseki(1): kaisuu = kaisuu + 1
End If
End If
Next
If kaisuu > 0 Then
y = wa / kaisuu
Picture2.Cls: Picture2.Print "m/(m+n)(0�`.49)="; r
Picture3.Cls: Picture3.Print "�ʐϔ� ="; y
If r = 0 Then
Picture1.PSet (0, -y), iro1
Else
Picture1.Line -(r, -y), iro1
End If
Write #1, r, y
End If
Next
Close #1
Picture1.Circle (1 / 3, -7), 0.0075, iro1
Picture2.Cls: Picture2.Print "�I�����܂����D"
Picture3.Cls: Picture3.Print "f(r)=(1-r+r^2)/(1-2r)^2�v���b�g"
For r = 0 To 0.5 - kizami Step kizami
If r = 0 Then
Picture1.PSet (0, -f(0)), iro0
Else
Picture1.Line -(r, -f(r)), iro0
End If
Next
Beep
End Sub
Private Sub Command2_Click()
End
End Sub
Private Function f(ByVal r As Double) As Double
f = (1 - r + r * r) / (1 - 2 * r) / (1 - 2 * r)
End Function
�f�[�^�im/(m+n)�C�ʐϔ�̏��ɕ���ł��܂��j
| 0 | .999970308041995 |
| .01 | 1.03091685088192 |
| .02 | 1.06385487187592 |
| .03 | 1.09878457255916 |
| .04 | 1.13607764696844 |
| .05 | 1.17592162576469 |
| .06 | 1.21849266823427 |
| .07 | 1.26406152168348 |
| .08 | 1.31292805408391 |
| .09 | 1.36540363718997 |
| .1 | 1.42189594130447 |
| .11 | 1.48274870707101 |
| .12 | 1.54851986034893 |
| .13 | 1.61960203408582 |
| .14 | 1.69677976519562 |
| .15 | 1.78061264811073 |
| .16 | 1.87188861228095 |
| .17 | 1.97178347863177 |
| .18 | 2.0810237524478 |
| .19 | 2.20338122742966 |
| .2 | 2.33105591333246 |
| .21 | 2.47950329959968 |
| .22 | 2.6415783921597 |
| .23 | 2.82205700046731 |
| .24 | 3.02366842506976 |
| .25 | 3.24842457985923 |
| .26 | 3.50521575781715 |
| .27 | 3.79442636580152 |
| .28 | 4.12387781168895 |
| .29 | 4.50203963716306 |
| .3 | 4.93767521461343 |
| .31 | 5.44392299757662 |
| .32 | 6.03659244737924 |
| .33 | 6.73787971424711 |
| .34 | 7.57442344991707 |
| .35 | 8.58765709035429 |
| .36 | 9.8163993417154 |
| .37 | 11.3445600805142 |
| .38 | 13.2866250591007 |
| .39 | ,15.7459066751137 |
| .4 | 19.000401013052 |
| .41 | 23.3980877733627 |
| .42 | 29.5477885954535 |
| .43 | ,38.5153295949182 |
| .44 | 52.3335906940583 |
| .45 | 75.2484176839521 |
| .46 | 117.436295851565 |
| .47 | 208.583294285575 |
| .48 | 469.000465047941 |

| NO.624 | '99 10/12 | Junko | �O�p�`�̖ʐρi�T�j |
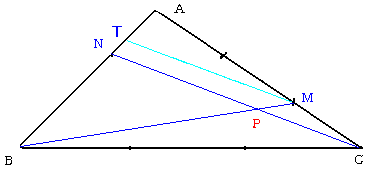
NO.619�ł́A�_�q�̈ʒu�x�N�g�������߂�̂Ƀx�N�g���̂P���Ɨ������g���܂����B
�u���l���E�X�̒藝�v�Ƃ����̂������āA������g���ċ��߂邱�Ƃ��ł��܂��B
����͓_�o�ł��܂��B
���}�̂悤�ɁA�_�l��ʂ�b�m�ɕ��s�Ȓ����l�s���Ђ��܂��B
�a�o�F�o�l���a�m�F�m�s���a�m�F�m�`�~(�l�b�^�`�b)
���F�P�|�����Q�F�P�~(1/3)
������A�����U�^�V�Ƌ��܂�܂��B
�]���āA�o�l��(1/7)�a�l�ƂȂ�A
�ȉ���NO.619�Ɠ��l�ł��B
��ʂɎO�p�`�`�a�b�̊e�ӂa�b�A�b�`�A�`�a�����F���ɓ��������ꍇ���l���܂��B
����Ɠ��l�ɁA�_�l��ʂ�b�m�ɕ��s�Ȓ����l�s���Ђ��܂��B
�a�o�F�o�l���a�m�F�m�s���a�m�F�m�`�~(�l�b�^�`�b)
���F�P�|�������F���~{��/(���{��)}
������A����(�����{���Q)�^(���Q�{�����{���Q)�Ƌ��܂�܂��B
�]���āA�o�l��{���Q�^(���Q�{�����{���Q)}�a�l�ƂȂ�܂��B
���`�a�b�̖ʐς��r�Ƃ���ƁA
���`�a�k�����a�b�l�����b�`�m��{���^(���{��)}�r
�Ώ̐��Ɛ�قǂ̌��ʂ���A
���a�k�q�����b�l�o�����`�m�p��{���^(���{��)}�{���Q�^(���Q�{�����{���Q)}�r
�]����
| ���o�p�q | ���r�|(���`�a�k�{���a�b�l�{���b�`�m)�{(���a�k�q�{���b�l�o�{���`�m�p) |
| ���r�|{���^(���{��)}�r��R�{{���^(���{��)}�{���Q�^(���Q�{�����{���Q)}�r��R | |
| ��{(���|��)�Q�^(���Q�{�����{���Q)}�r |

| NO.628 | '99 10/20 | ���̗��� | �O�p�`�̖ʐρi�U�j |
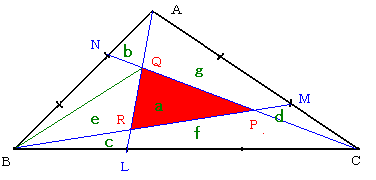
�O�p�`�̖ʐς̖��̓����i�ʐϔ�̗��p�j
���`�a�b�̖ʐς�X��P�Ƃ����B
�R�{�̐����ŋ��ꂽ�V�̕����̖ʐς��A
�O�p�`�o�p�q�����C�O�p�`�`�m�p�����C�O�p�`�a�k�q�����C�O�p�`�b�l�o�����C
�l�p�`�a�q�p�m�����C �l�p�`�b�o�q�k�����C�l�p�`�`�p�o�l�����@�Ƃ����B
�����`�k�C�a�l�C�b�m�͂��ꂼ��Εӂ��P�F�Q�ɓ������Ă���̂ŁA
���{���{�����P�^�R�C���{���{�����P�^�R�C���{���{�����P�^�R�@�@�ƂȂ�B
���̂R���𑫂��āA�@�Q�i���{���{���j�{���{���{�����P�@�@�ƂȂ�B
�V�̕�����S���������ʐς͎O�p�`�`�a�b������A
���{���{���{���{���{���{�����P�@�ł���B
���̂��Ƃ��A��Ɏ����������
�������{���{���@�c�@�ƂȂ�B
�܂��A�}�̑Ώ̐����A�����������@�ƌ�����B
�����ŁA���̖ʐς����߂܂��B
�����a�p�����ƁA�`�m�F�`�a���P�F�R�@���A
���`�a�p���R���`�m�p���R���@�ƂȂ�B
���ɁA���`�a�p�Ɓ��`�b�p���ׂ�ƁA
��ӂ`�p�͋��ʂŁA�����̔�͐����a�k�Ɛ����b�k�̔�ɓ������B
����āA�a�k�F�b�k���P�F�Q�@������A�ʐϔ��
���`�a�p�F���`�b�p���P�F�Q����A���`�b�p���Q���`�a�p���U���@�ł���B
�Ƃ��낪�A���`�m�p�{���`�b�p�����`�b�m���P�^�R
�����A���{�U�����P�^�R�@���@�@�̂Ɂ@�A�����P�^�Q�P�@
�S���A���l�ɂ��āA�������������P�^�Q�P�@��B
���������āA�������{���{�����P�^�V
�ȏォ��A���o�p�q���i�P�^�V�j���`�a�b�@�@�@�c�i�����j

 �߂�
�߂�