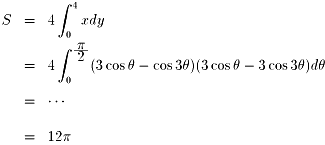
偲偄偆昗弨揑側抲姺愊暘偺寁嶼偱偡丏
偙偺栤戣傪師偺傛偆偵夝偄偨惗搆偑偄傞偺偱偡丏 偙偺夝摎偺偳偙偑堘偭偰偄傞偺偐丆偲偄偆偺偑幙栤側偺偱偡丏
Weekend Mathematics乛僐儘僉僂儉幒乛僥乕儅暿乛22.抲姺愊暘
| NO.482 | '99 5/20 | 昹揷丂柧枻 | 抲姺愊暘乮侾乯 |
俋俈擭偺戝嶃晎棫戝妛擖帋栤戣偱丆
乽嵗昗暯柺忋偵丆尨揰俷傪拞怱偲偡傞敿宎俀偺屌掕偝傟偨墌俠偲丆
偦傟偵奜懁偐傜愙偟側偑傜夞揮偡傞敿宎侾偺墌俠'偑偁傞丏
墌俠'偺拞怱偑(俁,侽)偵偁傞偲偒偺俠'懁偺愙揰偵報俹傪偮偗丆
墌俠'傪墌俠偵愙偟側偑傜妸傜偢偵夞揮偝偣傞丏
揰俹偺昤偔嬋慄偱埻傑傟偨椞堟偺柺愊傪媮傔傛丏乿
偲偄偆偺偑偁傝傑偟偨丏
夝摎偼丆
俹(倶丄倷)偲偟丆俷俙偺倶幉偲偺側偡妏傪兤偲偡傞偲丆
倶亖俁cos兤亅cos俁兤丆倷亖俁sin兤亅sin俁兤乮侽亝兤亙俀兾乯
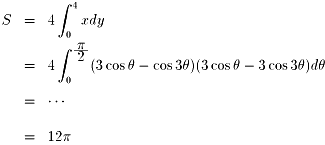
偲偄偆昗弨揑側抲姺愊暘偺寁嶼偱偡丏
偙偺栤戣傪師偺傛偆偵夝偄偨惗搆偑偄傞偺偱偡丏
偙偺夝摎偺偳偙偑堘偭偰偄傞偺偐丆偲偄偆偺偑幙栤側偺偱偡丏
| 儮俽 | 亖儮兤(倶2亄倷2)乛俀 |
| 亖儮兤{(俁cos兤亅cos俁兤)2亄(俁sin兤亅sin俁兤)2}乛俀 | |
| 亖儮兤(俆亅俁cos俀兤) |
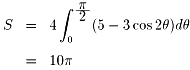

| NO.483 | '99 5/21 | Junko | 抲姺愊暘乮俀乯 |
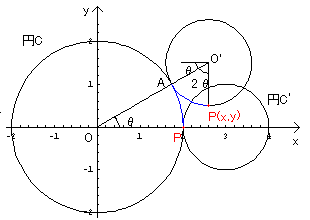
塃偺恾偺傛偆偵丄墌俠偲墌俠乫偲偺愙揰傪俙偲偡傞丅
俙俹偺挿偝偑摍偟偄偙偲偲丄墌俠偺敿宎偑丄墌俠乫偺敿宎偺俀攞偱偁傞偙偲傪
峫椂偡傞偲丄
x幉偲俷俙偲偺側偡妏兤偵懳偟偰丄佢俙俷乫俹偼俀兤偲側傞丅
廬偭偰丄P(x,y)偲偡傞偲丄
倶亖俁cos兤亄cos(兾亄俁兤)亖俁cos兤亅cos俁兤丆
倷亖俁sin兤亄sin(兾亄俁兤)亖俁sin兤亅sin俁兤
乮侽亝兤亙俀兾乯偲側傝傑偡丅
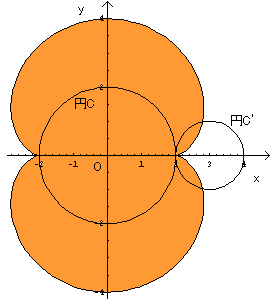
揰俹偺婳愓偼塃偺恾偺傛偆偵側傝傑偡丅
墌俠偲墌俠乫傕堦弿偵偐偄偰偁傝傑偡丅
栤戣偼僆儗儞僕偺晹暘偺柺愊傪媮傔傞偙偲偵側傝傑偡丅

| NO.486 | '99 5/21 | 悈偺棳傟 | 抲姺愊暘乮俁乯 |
NO.482偺屻偺夝摎偼丄
嬌曽掕幃丂倰亖倖乮兤乯偺柺愊傪媮傔傞岞幃偵
擖傟偰寁嶼偟偰偁傝傑偡偑丄
揰俹偲倶幉偲偺側偡妏偼兤偱偼偁傝傑偣傫丅
偩偐傜丄偙偙偱娫堘偭偰偄傑偡丅
偪側傒偵墌俠乫偼壗夞揮偟傑偡偐偼丄傕偆偍暘偐傝偱偟傚偆丅
俁夞揮偟傑偡丅
偙偺婳愓傪僄僺丒僒僀僋儘僀僪乮奜僒僀僋儘僀僪乯偲偄偄傑偡丅
墌俠乫傪撪懁偱丄墌俠偵愙偟側偑傜妸傞偙偲側偔夞揮偝偣傞偲丄
偙偪傜偼侾夞揮偟偐偟傑偣傫丅偦偟偰丄偙偺応崌偼墌俠偺撪晹偱
倷幉忋傪摦偔偙偲偵側傞偱偟傚偆丅
傑偨丄婳愓偺柤徧偼朰傟傑偟偨偑丄乮撪僒僀僋儘僀僪偲尵偄傑偡乯

| NO.488 | '99 5/22 | Junko | 抲姺愊暘乮係乯 |
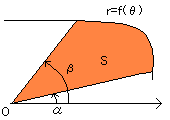
嬌嵗昗宯偵偍偗傞柺愊偺媮傔曽偱偡丅
尨揰偐傜偺嫍棧倰偑丄曃妏兤偺娭悢偲偟偰丄倰亖倖(兤)偲偟偰昞偝傟偰偄傞偲偒丄
嵍恾偺柺愊俽偼埲壓偺掕愊暘偵傛偭偰傕偲傔傞偙偑偱偒傑偡丅
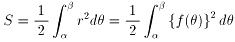
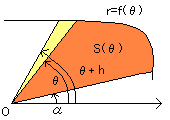
偳偆偟偰忋偺幃偱柺愊傪媮傔傞偙偲偑偱偒傞偺偐丄 姶妎揑偵偱偼偁傝傑偡偑偙偠偮偗偰傒傑偡丅


| NO.490 | '99 5/24 | Junko | 抲姺愊暘乮俆乯 |
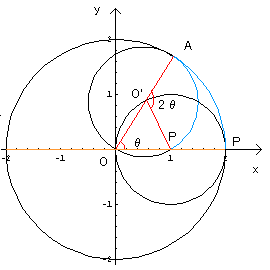
墌俠乫傪撪懁偱丄墌俠偵愙偟側偑傜妸傞偙偲側偔夞揮偝偣偨偲偒偺
婳愓偼丄乽僴僀億僒僀僋儘僀僪乿偲偄偆偦偆偱偡丅
揰俹偼倷幉忋傪(2,0)偐傜(-2,0)傑偱峴偒丄傑偨栠偭偰偒傑偡丅
(僆儗儞僕偺晹暘)
敿宎偺斾傪侾丗俀偲偡傞偲丄慄暘偵側偭偰偟傑偭偰偍傕偟傠偔側偄偺偱丄
崱搙偼敿宎偺斾傪侾丗俁偵偟偰傒傑偡丅
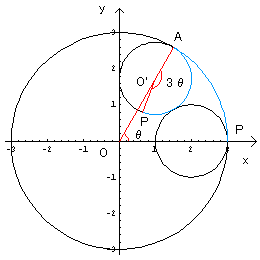
墌俠偲墌俠乫偲偺愙揰傪俙偲偟傑偡丅
俙俹偺挿偝偑摍偟偄偙偲偲丄墌俠偺敿宎偑丄墌俠乫偺敿宎偺俁攞偱偁傞偙偲傪
峫椂偡傞偲丄x幉偲俷俙偲偺側偡妏兤偵懳偟偰丄佢俙俷乫俹偼俁兤偲側傞丅
廬偭偰丄P(x,y)偲偡傞偲丄
倶亖俀cos兤亄cos(亅俀兤)亖俀cos兤亄cos俀兤丆
倷亖俀sin兤亄sin(亅俀兤)亖俀sin兤亅sin俀兤
乮侽亝兤亙俀兾乯偲側傝傑偡丅
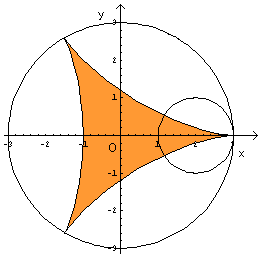
偙傟傪恾帵偡傞偲偙偆側傝傑偡丅
偙偺嬋慄偱埻傑傟偨晹暘偺柺愊傕媮傔偰傒偰偔偩偝偄丅

| NO.491 | '99 5/24 | 昹揷丂柧枻 | 抲姺愊暘乮俇乯 |
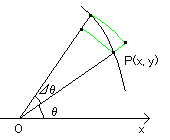

偙傟傪偄偮傕偺傛偆偵俛俙俽俬俠偺僾儘僌儔儉偱専徹偟傑偟偨丏愄偺榖側偺偱丆俶俉俉擔杮岅俛俙俽俬俠偱嶌偭偰偁傝傑偡丏
100 'SAVE"97OOSAK3.BAS",A 110 *INIT:SCREEN 3,0,1:CLS 3:SCREEN ,,0,1:CLS 3:CONSOLE 0,25,0,1:WIDTH 80,25 120 ON STOP GOSUB *STP:STOP ON:ON ERROR GOTO *ER 130 DIM X(180),Y(180):LOCATE 44,12:PRINT"俋俈擭戝嶃晎棫戝" 140 R=2:RR=1 '戝墌丆彫墌偺敿宎 150 X0=0:Y0=0:X1=X0+R+RR:Y1=Y0:S1=0:S2=0:S3=0:S4=0:S5=0 160 T=0:X(0)=X1-RR:Y(0)=Y1:KK=49:XC=320+2*KK:YC=200:ACT=0:PI=3.14159:W=PI/180 170 ' 180 *ST:GOSUB *SAKUZU 190 LOCATE 0,0:PRINT"壗偐僉乕傪墴偟偰壓偝偄丏巒傔傑偡丏" 200 WHILE INKEY$="":WEND:WHILE INKEY$<>"":WEND:LOCATE 0,0:PRINT SPC(34) 210 FOR T=0 TO 180:TT=2*T 220 X1=X0+(R+RR)*COS(TT*W):Y1=Y0+(R+RR)*SIN(TT*W) 230 X(T)=X1-RR*COS((RR+R)*TT*W):Y(T)=Y1-RR*SIN((RR+R)*TT*W) 240 ON -(T=0) GOTO 320 250 S1=S1+.5*ABS((Y(T)-Y(T-1))*(X(T)+X(T-1))) 260 S2=S2+.5*ABS(X(T-1)*Y(T)-X(T)*Y(T-1)) 270 A=SQR(X(T)*X(T)+Y(T)*Y(T)):B=SQR(X(T-1)*X(T-1)+Y(T-1)*Y(T-1)) 280 C=SQR((X(T)-X(T-1))*(X(T)-X(T-1))+(Y(T)-Y(T-1))*(Y(T)-Y(T-1))) 290 S=.5*(A+B+C):S3=S3+SQR(S*(S-A)*(S-B)*(S-C)) 300 S4=S4+.5*A*B*SIN(2*W) 310 S5=S5+.25*(A*A+B*B)*2*W 320 ACT=1-ACT:DISP=ACT*16+1:SCREEN ,,ACT:CLS 2 330 GOSUB *SAKUZU:LOCATE 0,4:PRINT"t=";TT;"亱":PRINT 340 COLOR 2:PRINT"柺愊亖4佺(0,4)xdy":PRINT USING" 亖##.####*兾";S1/PI:PRINT 350 PRINT"柺愊亖嚁.5*abs(x1*y2-x2*y1)":PRINT USING" 亖##.####*兾";S2/PI:PRINT 360 PRINT"柺愊亖嚁(僿儘儞偺岞幃)":PRINT USING" 亖##.####*兾";S3/PI:PRINT 370 PRINT"柺愊亖嚁.5*OP1*OP2*sin(嚈t)":PRINT USING" 亖##.####*兾";S4/PI:PRINT 380 PRINT"柺愊亖嚁.5*OP^2*嚈t":PRINT USING" 亖##.####*兾";S5/PI:COLOR 7 390 SCREEN ,,,DISP 400 ON -(INKEY$="S") GOSUB *SS 410 NEXT:WHILE INKEY$<>"":WEND 420 LOCATE 0,0:PRINT"孞傝曉偟傑偡偐丠乮倄乛俶乯":A$="" 430 WHILE A$<>"Y" AND A$<>"y" AND A$<>"N" AND A$<>"n" 440 A$=INKEY$:WHILE INKEY$<>"":WEND 450 WEND 460 IF A$="Y" OR A$="y" THEN RUN 470 LOCATE 0,0:PRINT"廔傢傝傑偟偨丏 " 480 ' 490 *STP:END 500 ' 510 *ER:RESUME NEXT 520 ' 530 *SAKUZU:CIRCLE(XC+KK*X0,YC-KK*Y0),KK*R,7 540 CIRCLE(XC+KK*X1,YC-KK*Y1),KK*RR,6 550 FOR J=0 TO T:CIRCLE(XC+KK*X(J),YC-KK*Y(J)),2-(J=T),2-3*(J=T),,,,F:NEXT 560 RETURN 570 ' 580 *SS:WHILE INKEY$="":WEND:WHILE INKEY$<>"":WEND:RETURN偙偺僾儘僌儔儉偵傛傞偲丆
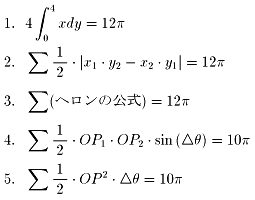
偲側傝傑偡丏
1.偼捠忢偺愊暘寁嶼丆2乣4偼尨揰傪侾偮偺捀揰偲偟丆
偦偺捀揰偺妏傪俀搙乮亖兾乛俋侽乯偲偡傞旝彫偺嶰妏宍偵暘妱偟偰
柺愊偺榓傪媮傔偨寁嶼丆5偼尨揰傪拞怱丆
拞怱妏俀搙偺旝彫偺愵宍偵暘妱偟偰柺愊偺榓傪媮傔偨寁嶼偱偡丏
偙傟偱偳偆傗傜嚈兤乮亖俀搙乯偑偐傜傫偩寁嶼偩偲侾侽兾偵側傝丆
偦偆偱側偄偲侾俀兾偵側傞偙偲偑暘偐傝傑偟偨丏
偟偐偟偳傟傕摨偠晹暘偺柺愊傪媮傔傞幃偺偼偢偱偡丏
偙偙傜曈偱摢偑偙傫偑傜偑偭偰偟傑偭偨偺偱偡丏
偳偆偐奆偝傫丆彆偗偰壓偝偄丏
懠偵儌儞僥僇儖儘朄偱傕僾儘僌儔儉傪嶌偭偰傒偨偺偱偡偑丆
柺愊偼侾俀兾偵側傝傑偟偨丏
惓夝偼愨懳偵侾俀兾偲偄偆帠偼暘偐偭偰偄傞偺偱偡偑丒丒丒丏

| NO.494 | '99 5/25 | 悈偺棳傟 | 抲姺愊暘乮俈乯 |
NO.490偵偁傞僴僀億僒僀僋儘僀僪偱埻傑傟偨恾宍偺 柺愊傪媮傔偰傒傑偟偨丅


| NO.495 | '99 5/25 | Junko | 抲姺愊暘乮俉乯 |
NO.491偵偁傞丄儌儞僥僇儖儘朄偵偮偄偰
僐儊儞僩偟傑偡丅
偁傞恾宍俙偺柺愊傪媮傔傞偺偵丄偦傟傪娷傓惓曽宍俛傪峫偊傑偡丅
偙偺惓曽宍偺拞偐傜擟堄偺揰俹(x,y)傪拪弌偟偰丄偦偺揰俹(x,y)偑
恾宍俙偺拞偵偁傞偐偳偆偐傪敾抐偟傑偡丅
偙傟傪1,000夞孞傝曉偟偰俙偺拞偵偁偭偨夞悢偑偨偲偊偽521夞偲偡傞偲丄
(俙偺柺愊)/(俛偺柺愊)佮521/1,000偲峫偊傜傟傞傢偗偱偡丅
偙偆偟偰俙偺柺愊偺嬤帡抣傪媮傔傜傟傞傢偗偱偡偑丄
帋峴夞悢傪10,000丄100,000偲傆傗偡(僐儞僺儏亅僞亅偑偁傟偽偙偦丒丒丒)偙偲偱丄
偁傞掱搙偺惛搙傪摼傞偙偲偑偱偒傞傢偗偱偡丅
昹揷丂柧枻偺NO.448側偳偼
偦偺椺偩偲巚偄傑偡丅
偙偺儌儞僥僇儖儘朄偲偄偆偺偼乽戝悢偺朄懃乿偺婎偯偄偰偄傑偡丅
乽戝悢偺朄懃乿偲偄偆偺偼丄帋峴夞悢俶傪廫暘戝偒偔偡傞偲丄帠徾俙偺婲偙傞憡懳搙悢
倰乛俶偼傎傏俹(俙)偵摍偟偄丄偲偄偆傕偺偱偡丅
偦傟偵偟偰傕側偤丄乽儌儞僥僇儖儘乿側偺偱偟傚偆丠

| NO.499 | '99 5/26 | 悈偺棳傟 | 抲姺愊暘乮俋乯 |
儌儞僥丒僇儖儘朄偵偮偄偰丄戝嶃彂愋敪峴偺乽怴悢妛帿揟乿偐傜堷梡偟傑偡丅
廫暘妸傜偐側嫬奅儭偱埻傑傟偨椞堟兌偵偍偄偰丄
儭忋偵嫬奅抣傪梌偊偰儮倳亖侽傪夝偔僨▋妰N儗栤戣偺夝倳偺掕揰倶伕兌
偵偍偗傞抣倳乮倶乯偼丄倶偐傜弌敪偟偰儔儞僟儉偵摦偔揰
乮埲壓偙傟傪乽傛偭傁傜偄乿偲屇傇乯
偑嫬奅倷偵偍偄偰偮偐傑傞妋棪枾搙傪倫倶乮倷乯偲偡傞偲丄
愊暘佺冋乮倷乯倓倫倶乮倷乯丂偱梌偊傜傟傞丅
偙傟偼杮幙揑偵侾俋俀侽擭戙偵僂▉[僫乕
乮晝偐傜揤嵥嫵堢傪庴偗丄侾俉嵨偱僴乕僶乕僪戝妛懖嬈丄僽儔僂儞塣摦偱桳柤乯
偵傛偭偰尋媶偝傟偨寢壥偱偁傝丄晄惓懃揰傗僂▉[僫乕偺忦審側偳丄
偙偺棫応偐傜柧夣偵愢柧偝傟傞丅
侾俋俆侽擭戙埲崀妋棪榑揑億僥儞僔儍儖榑偺傕偭偲傕娙扨側堦椺偲偟偰
抦傜傟傞傛偆偵側偭偨丅
偄傢偽傛偭傁傜偄偑倷偱偮偐傑傞偲冋乮倷乯偺敱嬥傪偲傜傟傞偲偒丄
倶偐傜弌敪偟偨傛偭傁傜偄偑偲傜傟傞敱嬥偺婜懸抣偑倳乮倶乯偲偄偆偙偲偱偁傞丅
偙傟傪儔儞僟儉偵摦偔揰傪僔儏儈儏儗乕僩偟傚偆偲偄偆偺偑
儌儞僥丒僇儖儘朄偵傛傞嫬奅抣栤戣偺夝朄偱偁傞丅
採埬偝傟偨摉帪乮侾俋係侽擭枛乯偵偼婏敳側夝朄偲昡敾偱偁偭偨偑丄
徻偟偄抣傪媮傔傞偵偼偒傢傔偰懡悢夞偺斀暅傪梫偟偨丅
偦偙偱丄巹偺尒夝偱偡偑丄摉帪丄僀僞儕儎偺儌僫僐偺嬤偔偵偁偭偨
儌儞僥僇儖儘偲偄偆挰傪弰偭偰峴傢傟傞帺摦幵偺儔儕乕偑偙偺傛偆側丄
儔儞僟儉塣摦傪偟偨偙偲偐傜丄偙偺偄傢傟傪庢傞傛偆偵側偭偨偲峫偊傜傟傞丅
慡偔偺悇應偱偡偑丠

| NO.502 | '99 5/27 | 悢妝幰 | 抲姺愊暘乮侾侽乯 |
儌儞僥僇儖儘朄偼丄棎悢傪梡偄偨庤朄堦斒偵晅偗傜傟偨柤慜偱偡丅
棎悢傪梡偄傞偲偼丄偁傞堄枴偱僒僀僐儘傪怳傞偙偲偵懳墳偟傑偡丅
偦偙偱丄搎攷偱桳柤側応強乽儌儞僥僇儖儘乿乮俥侾偱傕桳柤偱偡乯傪偲偭偰丄
儌儞僥僇儖儘朄偲柤偯偗傑偟偨丅乮幵偺儗乕僗偱偼側偄偱偡丅乯
僐儘僉僂儉偱傕徯夘偝傟偰偄傑偡偑

| NO.503 | '99 5/28 | 昹揷丂柧枻 | 抲姺愊暘乮侾侾乯 |
儌儞僥僇儖儘朄偵偮偄偰偱偡偑丆
兾傪媮傔傞僾儘僌儔儉偼偄傠偄傠側尵岅偺夝愢彂偵嵹偭偰偄傑偡丏
崱夞偺戝嶃晎棫戝妛偺栤戣偺摎傪媮傔傞僾儘僌儔儉偼師偺捠傝偱偡丏
偙傟偼俻俛俙俽俬俠偱嶌偭偰偁傝傑偡丏
俻俛俙俽俬俠偼倂俬俶俢俷倂俽俋俉傗俋俆偺僔僗僥儉俠俢俼俷俵偺拞偺
俷俴俢俵俽俢俷俽偲偄偆僼僅儖僟偺拞偵偁傝傑偡丏
偙偺僼僅儖僟偺拞偺僼傽僀儖傪偡傋偰僴乕僪僨傿僗僋偵僐僺乕偟丆
俢俷俽僾儘儞僾僩傪棫偪忋偘丆倀俽儌乕僪偵偟偰丆
俻俛俙俽俬俠傪棫偪忋偘傟偽俷俲偱偡丏
嬶懱揑偵巹偺応崌偩偲偙偆偟偰偄傑偡丏
俢俷俽僾儘儞僾僩傪棫偪忋偘丆
丂丂>cd \qbasic (+enter)丂乮俻俛俙俽俬俠偲偄偆僼僅儖僟偺拞偵廂擺偟偰偁傝傑偡乯 丂丂>us (+enter)丂丂丂丂丂乮倀俽儌乕僪偵偟傑偡乯 丂丂>qbasic (+enter)丂丂丂乮俻俛俙俽俬俠傪棫偪忋偘傑偡乯偲偄偆晽偵偟傑偡丏廔傢偭偨傜丆
丂丂>jp (+enter)丂丂丂丂丂乮擔杮岅儌乕僪偵栠偟傑偡乯 丂丂>exit (+enter)丂丂丂丂乮俢俷俽僾儘儞僾僩偐傜栠傝傑偡乯偱偡丏偙傫側栶棫偮僾儘僌儔儉尵岅偑俋俉傗俋俆偵昗弨憰旛偝傟偰偄傞 乮偮傑傝偨偩偱乯偲偼丆偡偽傜偟偄尷傝偱偡丏 偙傟偼堦愄慜偺俻倀俬俠俲丂俛俙俽俬俠偲摨偠偲峫偊偰偄偄偱偟傚偆丏
'97oosaka.qb SCREEN 12: CLS : RANDOMIZE TIMER kk = 49: xc = 320 + 2 * kk: yc = 200: pi = 3.14159: w = pi / 180 iro0 = 7: iro1 = 2: max = 1000000 DEF fnx (x) = xc + kk * x: DEF fny (y) = yc - kk * y n = 0: k = 0: t1$ = "Press any key to start": t2$ = "Press any key to quit" LINE (fnx(2 * SQR(2)), fny(4))-(fnx(-2 * SQR(2)), fny(-4)), iro0, B PSET (fnx(2), fny(0)), iro1 FOR t = 1 TO 360 LINE -(fnx(3 * COS(t * w) - COS(3 * t * w)), fny(3 * SIN(t * w) - SIN(3 * t * w))), iro1 NEXT: PAINT (fnx(0), fny(0)), iro1 LOCATE 1, 1: PRINT t1$ WHILE INKEY$ = "": WEND: WHILE INKEY$ <> "": WEND LOCATE 1, 1: PRINT SPC(LEN(t1$)); LOCATE 28, 1: PRINT t2$ WHILE n <= max AND INKEY$ = "": n = n + 1 k = k - (POINT(fnx(2 * SQR(2) * (2 * RND - 1)), fny(4 * (2 * RND - 1))) = iro1) s = k / n * 2 * SQR(2) * 2 * 4 * 2 LOCATE 1, 1: PRINT n; "kai shikou" PRINT USING "S=###.###### * pi"; s / pi WEND LOCATE 28, 1: PRINT SPC(LEN(t2$)); : END丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂

| NO.527 | '99 6/9 | 悈偺棳傟 | 抲姺愊暘乮侾俀乯 |
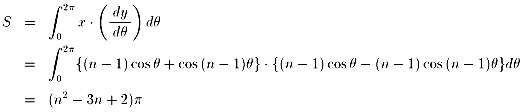
偝傜偵丄値亖俁偺偲偒丄摿偵僨儖僩僀僪丄
値亖係偺偲偒丄摿偵傾僗僥儘僀僪丂偲尵偄傑偡丅
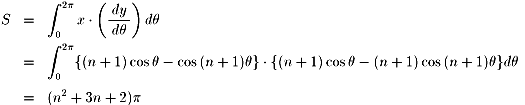
偝傜偵丄値亖侾偺偲偒丄僇乕僕僆僀僪乮怱憻宍乯丄
値亖俀偺偲偒丄僱僼儘僀僪乮恡憻宍乯偲尵偄傑偡

 栠傞
栠傞