
Weekend Mathematics/コロキウム室/テーマ別
/21.xn+yn=zn
NO.443 '99 4/19 プ−太 xn+yn=zn(1)
問題3「らせん階段の問題」のコメント欄に
フェルマ−の最終定理と書かれてあります。
nが3以上の自然数の場合、
「xn+yn=zn」を満たす整数x、y、zは存在しない。
(n=2のときには、ピタゴラス数といって整数解x、y、zは無限に存在し、 その整数解の公式が知られている)
僕が研究した成果は、以下のみです。
nが-3のとき、
x-3+y-3=z-3
両辺に(xyz)3をかけて、
(yz)3+(zx)3=(xy)3
ところが、整数解x、y、zが存在したとすると、フエルマーの大定理に矛盾。
よって、整数解は存在しない。
同様に、nが-4以下の整数のときも、整数解は存在しません。


NO.445 '99 4/20 Junko xn+yn=zn(2)


NO.456 '99 5/2 プ−太 xn+yn=zn(3)


| NO.470 | '99 5/12 | 月の光 | xn+yn=zn(4) |
問題
フェルマーの定理を n=3,4,5… のときなど、
できる範囲で証明してください。
ただし、x,y,z は自然数とします。
n=4 のときに挑戦してみました。
x4+y4=z4 を満たす自然数 x,y,z は存在しない。
証明) x,y,z は自然数なので x<z,y<z …(1)
x4=z4-y4=(z2+y2)(z+y)(z-y)
(1)より x2<z2<z2+y2
だから x3=z2+y2 …(2)
または x4=z2+y2 …(3)
(2)のとき、(1)より x<z<z+y なので x=z-y , z+y=1
これは zとyが自然数なので有り得ない。
(3)のとき、z2-y2=1 , z2=y2+1
しかし、y2<y2+1<y2+2y+1 から
y<
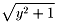 <y+1
<y+1
yは自然数なので z2=y2+1 を満たす自然数 z は存在しない。
よって x4+y4=z4 を満たす自然数
x,y,z は存在しない。

| NO.472 | '99 5/14 | プ−太 | xn+yn=zn(5) |
NO.470の
x4+y4=z4 を満たす自然数 x,y,z は存在しない
という証明の以下の部分について、大変恐縮ながら
間違った証明をされているものと思われます。
x,y,z は自然数なので x<z,y<z …(1)式の因数分解は、そのまま数の素因数分解になってはいません。 z2+y2は、例えば(x3.5)とか (x4)/3かもしれません。 ただし、もちろん (x3.5)とか(x4)/3が整数であった場合ですが。
x4=z4-y4=(z2+y2)(z+y)(z-y)
(1)より x2<z2<z2+y2 だから x3=z2+y2 …(2)
または x4=z2+y2 …(3)
フェルマーの大定理のn=3,4のときの証明が、
初等整数論講義(高木貞治)にのってあります。
大学2,3年生のレベルだと思われます。
もし、証明をこのコロキウムに
載せるためには、準備と証明自身で、
(本に換算して)10ページ前後必要だと思われます。
ちなみに、初等整数論講義(高木貞治)では二次体をつかって
証明してあります。

 戻る
戻る