Weekend Mathematics/コロキウム室/テーマ別
/20.最速降下問題2
コロキウム室(最速降下問題・その2)
| NO.1162
| 2002.3.1. | DDT | 最速降下問題(12)
|
ラグラジアンとハミルトニアンン形式に基づく力学の定式化について、一通り頑張ってみます。
- ラグラジアン形式の力学
1自由度運動に限定します。
この中には、NO.1158の二次元空間の中の1次元曲線に束縛されるような運動も含みます。
要するに運動を表すために、一個の位置座標しか必要ないということです。
それが1自由度の意味です。運動を決定する母関数のようなものを考えます。
それをLとし、ラグラジアンと呼びます。運動を決定するLとはどんなものなのか?
参考文献[1]の受け売りによれば、
運動の各瞬間の位置と速度を全て与えれば、運動は定まる. (1)
ので、
L=L(v、x、t) (2)
で必要十分です。ここでtは時間、xはその時の位置座標,vはその時のその位置での速度。
多くの場合エネルギー保存則が成り立ちます。mを粒子の質量,U(x)を力のポテンシャルとして、
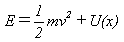 (3)
(3)
式(3)は、速度と位置の関係が時間と無関係に定まることを示します。
ラグラジアンLは運動を決めるものなので、(2)が時間tを陽に含むならば、
vとxの関係も時間に依存し(3)は成り立ちません。従ってエネルギー保存則が成立する場合は、
L=L(v、x) (4)
です。これを保存系と呼びます。保存系のラグラジアンは、
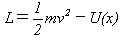 (5)
(5)
であり、運動方程式がラグランジュ方程式、
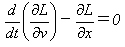 (6)
(6)
であることはすぐにわかります。ここで∂L/∂vの意味は
、L(v,x)のvとxを別々の変数とみなしたvでの偏微分の意味で、
その外側のd/dtは、vとxを時間の関数v(t),x(t)とみての微分です。やります。
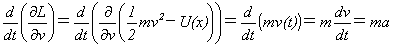 (7)
(7)
式(7)の最後のaは、加速度を表します。∂L/∂xも∂L/∂vと同じ意味で、
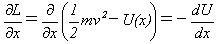 (8)
(8)
となり、式(6)は保存系の通常の運動方程式、
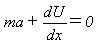 (9)
(9)
に一致します。通常の座標を使う限り、ラグラジアンを用いる方法はたんに面倒なだけですが、
任意に変換された座標でもラグランジュ方程式(6)がそのままの形で成り立つところに意味があります。
No.1158の最速降下問題を例にとります。通常の(x,y)座標での系の全方程式は以下となります。
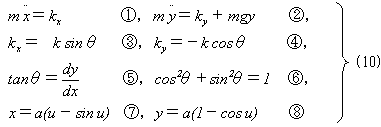
ここで・は時間に関する微分,kは運動を束縛する最速降下線から、
その内法線方向に粒子が受ける抗力です。未知数の数と条件数を勘定してみると
過不足はありませんが、とても扱い切れそうにありません。
こうなった理由は、座標(x,y)が独立でないからです。式(10)-①,②は(x,y)
に関する運動方程式でこれが解ければ良いのですが、(x,y)が独立でないために(x,y)
を関係付ける抗力kが入ってきます。抗力kを束縛曲線の形から定めるために、
その後6本もの式が必要になります(式(10)-③~⑧)。
運動が1自由度なのは明らかなので、束縛曲線の形を定める式(10)-⑦,⑧のパラメーターuを、
最初から運動の座標にとってやるべきです。式(10)-⑦,⑧を出発点にとれば、
{(x,y)}空間で運動軌道が最速降下線になることは自明なので、抗力kは不要です。
x(t),y(t)が欲しければ、uに関する運動方程式からu=u(t)を得たあとで、
u(t)を式(10)-⑦,⑧へ単に代入するだけでx(t),y(t)を得られます。実際にやってみます。
運動エネルギーをT,位置エネルギー(力のポテンシャル)をUとして、式(10)-⑦,⑧より、
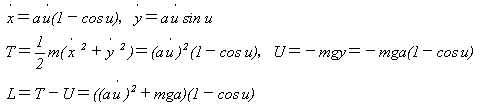
となりますが、式(6)はどんな座標でも成り立ちます。
1-cos u=2sin2(u/2)であることに注意して、
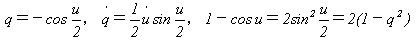
と変換すると、
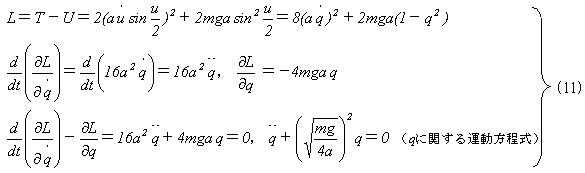
となり、qに関する単振動の式が現れます。
ここから最速降下線振り子の等時性や振動周期は一気に片づきますが、
この変換はNO.1160のyokodonさんを見て気づきました(超有名題なのでたぶん常識)。
問題が解けてしまえば作用変数もクソもありません。
最適な変数変換や置換に関して、人間の目に優るものはありません・・・。
そして最適な変数が選ばれた時、ラグラジアン形式はすごい威力を発揮します、
と苦しい言い訳をするしかありません・・・苦しいよ~~。
もちろんqに関する運動方程式は、式(10)からよけいな未知数を順次消去して同じ変換を行っても
得られるはずですが、明らかに非常に難儀です。少しでも問題が複雑になると、
運動方程式を立てるのすら困難になる場合は多々あります。
それに対してラグラジアンを用いた式(11)の方法では、微分計算と、
変数を書きかえる代入計算だけでことは済みます。この2つはやれば必ずできるものです。
また1自由度以上の多自由度運動や連続体力学まで考えれば、
ラグラジアン形式は手放せなくなります。
ラグランジュ方程式(6)が任意の座標変換で形を変えないことは、通常の座標xが、
x=x(q、t) (2)
と一般化座標qに変換されたとして、速度dx/dtを一般化速度dq/dtによって表わした、
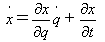 (13)
(13)
などを式(6)に直接代入して示すこともできますが、
もっと重要なことは、式(6)が変分原理を導くことです。
式(6)は、NO.1150-[4]のオイラーラグランジュ方程式と全く同じものです。
それは同式で、y → x,y' → v,微分パラメーターとしてx → tと読みかえれば明らかです。
よってNO.1150-[3]よりラグランジュ方程式(6)は、定積分、
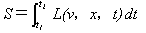 (14)
(14)
を最小化するものです。定積分Sは作用積分と言われ、
作用積分を最小化してラグランジュ方程式から運動方程式を導くことを、
最小作用の原理と言います。オイラーラグランジュ方程式は、
Lの具体的関数形に依存していません。従ってそれがどのような座標で書かれていようと
常に同じ形になり、そのとき定積分(14)は最小になります。
よってラグランジュ方程式(6)は、任意の座標で不変です。
また式(14)のLが時間tを陽に含んでも良いことから、
最小作用の原理は保存系以外の運動にも成り立ちます。
- ハミルトン形式の力学
ラグラジアン形式は、運動方程式を座標の2階微分方程式として与えます(式(11)の最下段のように)。
2階微分方程式は、1階の連立微分方程式に分解できます。2階微分方程式としての運動方程式を、
運動の解析に特に適した形で、系統的に連立1階微分方程式へ分解する方法が、ハミルトン形式です。
参考文献[2]の受け売りをすれば「そのようなことをしても物理的に新しい内容がつけ加わるわけ
ではない」のですが「理論的見通しが良く」なります。
プロではないので「理論的見通し」の効果について、即座に適当な例は出てきません。
そこで我田引水な感覚でいうと、少なくとも式(10)と(11)くらいの違いはあります。
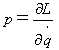 (15)
(15)
で一般化運動量pを定義します。ここでラグラジアンLは、L=L(dq/dt,q,t)です。
pが運動量と呼ばれるのは式(5),(6)より、通常の座標では∂L/∂v=mvで運動量p=mvだからです。
式(15)で式(6)を書きかえると運動方程式は、
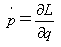 (16)
(16)
となります。いまのところ運動を決定するのはラグラジアンなので、
Lから出発してハミルトン形式を導きます。L=L(dq/dt,q,t)の全微分をとります。
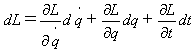 (17)
(17)
式(17)に(15),(16)を代入し、
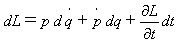 (18)
(18)
を得ます。式(18)の右辺第1項を、積の微分公式、
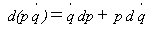 (19)
(19)
を利用して消去します。
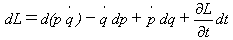 (20)
(20)
式(20)の右辺第1項を左辺へ移項し、全体の符号を変えれば、
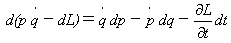 (21)
(21)
が得られます。以上の変形の目的はこうです。
運動方程式を連立1階微分方程式に分解する最も単純な方法は、
式(15),(16)で(p,q)を通常の運動量,座標とすれば明らかですが、
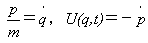 (22)
(22)
とすることです。しかしこの形は任意の座標で不変ではありません。
そこでラグラジアン形式を利用して、任意の座標で不変な分解法を得ることが目的です。
ただし式(22)の未知数は、速度dq/dtと座標qではなく、運動量pと座標qとみなすべきです。
dq/dtはたんに座標qの時間微分として微分方程式の中に現れただけです。
いいかえれば式(22)の目的は、2つの未知関数p(t)とq(t)を求めることです。
それが分解の意味です。従ってラグラジアンLを(p,q,t)の関数に変形する必要があります。
しかもそれは運動方程式(15),(16)の組を満たす必要があります。
Lの全微分を持ち出したのは、式(15),(16)にLの偏微分が出てくるからです。
またLの全微分から不要な未知数の微分であるd(dq/dt)を消去して、
dq/dtを含まないLの変形を与えることが、式(19)の最大の目的です。
式(21)の右辺は何らかの関数の(p,q,t)に関する全微分になっています。
よって(21)の左辺は、dH(p,q,t)とおけます。H(p,q,t)の全微分を正直に書いてやれば、
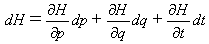 (23)
(23)
が得られます。式(23)と(21)の右辺の係数を比較することにより、
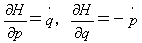 (24)
(24)
となります。式(24)をハミルトン方程式または正準方程式といい、Hをハミルトニアンと呼びます。
ハミルトン方程式の導出は、座標変換に対して不変な関係式(15),(16)と
恒等式(17),(19),(23)のみ用いたので、任意の座標で不変です。
式(15),(16)を使っているので、式(24)は運動方程式の成立する必要条件です。
十分条件でもあることは、通常の座標と運動量でエネルギーEをE=p2/2m+U(q,t)と書き直し、
H=E(p,q,t)とおいて(24)に代入すれば式(22)が得られ、
(24)が任意の座標で不変な関係であることから明らかです。
従ってハミルトニアンHはエネルギーEに等しくなります
(一般には保存しませんし、式(15)をdq/dtについて解いたのち、
(p,q,t)で表したdq/dtを用いてE(dq/dt,q,t)をE(p,q,t)に書き直す必要もあります)が、
このことはふつう、式(21)の左辺を式(15)を用いて一般化座標qで書き下し、
直接代入計算して示されます。
ここでのハミルトン方程式の誘導は主に参考文献[1]に従いました(一番とっつき易い思われます)。
定式化としては他に、式(21)の左辺のd()内を直接ハミルトニアンの定義とする方法もあります。
これをルジャンドル変換といい、参考文献[2]ではこれを採用しています。
参考文献[5]では、ルジャンドル変換の数学的意味と目的,ラグラジアンに対するハミルトニアン
の正体を、最も明快に与えてくれたと思われますが、私には難かし過ぎました
(ベクトル束の余接バンドルへの変換?)。
参考文献[4]は、同じことをもっと初等的に説明してくれましたが、
逆に意味の明瞭さが失われたと思います。以上、個人的感想でした。
式(24)は任意の座標変換よりも広い変換、
q=q(P,Q,t),p=p(P,Q,t) (25)
に対して不変性を持っています。ここで(P,Q)は新しい一般化運動量と一般化座標です。
ただし完全に任意ではなく制約条件が付きます。
(24)の形を不変に保つ一般化運動量と一般化座標の定め方が、正準変換論です。
正準方程式の名はそこから来てますが、正準変換を求めるときにも変分原理が必要になります。
それは式(14)の適当な変形から得られます。
またこのとき一般化運動量と一般化座標は正準共役量と呼ばれます。
NO.1158の作用-角変数は正準共役量の一つで、定義自体は正準変換の一応用にすぎませんが、
本来は正準変換を利用した摂動論用に開発されたものです(ということを知ってるだけです。
本の目次を見ればわかりますから・・・)。これ以上頑張ると大嘘を書きそうなので、
最後に参考文献をあげて終わります。
参考文献
[1]力学,ランダウ=リフシッツ,東京書店.
[2]古典力学,ゴールドスタイン,吉岡書店.
[1][2]は少々古いかもしれませんが、世界中で最も愛された(?)標準的テキストと思います。
[3]解析力学,大貫義郎,岩波書店.
[1][2]の解析力学関連のエッセンスが解説されてます。
[4]古典力学の数学的方法,アーノルド,岩波書店.
すでに現代風古典力学の現代的古典だと思います。個人的には多様体のチャートとアトラスで挫折しました。
[5]数学-その形式と機能,マックレーン,森北出版.
力学関係以外にも、読んで損はない本と思いますが、分厚いのと高額なのが食指を遠ざけます。

| NO.1344
| 2003.1.9. | Hkeisuke | 最速降下問題(13)
|
投稿を見ていて最速降下問題に関するものがありましたが、これは、mg(一定)という力場での最速降下線を見つける問題でした。
そこで他の力場でも同じような問題が考えられるのではないかと思い、万有引力
の場合ではどうなるかを考えていたのですが、どうもうまくいかないので、考え
てみてほしいです。問題を文にすると、
万有引力下で、ある点Aから点Bに移動するのに最短の時間で移動するような曲線
を求めよ。
ということです。

| NO.1354
| 2003.2.4. | DDT | 最速降下問題(14)
|
とりあえず、最後は逃げました。
[NO.1344 最速降下問題(13)の続き]
逆二乗力作用下(万有引力,重力)での最速降下線問題にトライします。
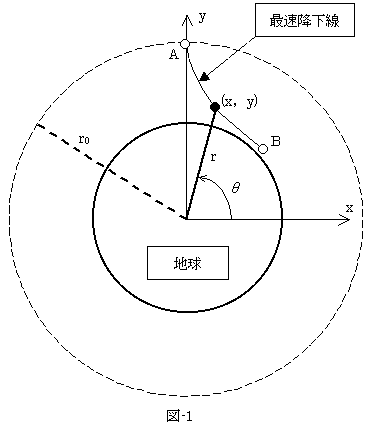
1.問題のスケッチ
図-1のように地球の中心に原点を持つ(x,y)座標系をとり、その原点を中心とする極座標系を(r,θ)とします。
まず地球の重力ポテンシャルは、極座標の動径rを用いて、
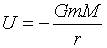 (1)
(1)
と書けます。ここでGはニュートンの重力定数,mは最速降下線を降下する点の質量,Mは地球の質量です。式(1)のポテンシャルの零点は、無限遠にとっています。
ポテンシャルの零点はどこにとっても良いので、図-1の最速降下線の開始点Aのある半径r0をポテンシャルの零点とします。零点をこのように選ぶと(1)は、
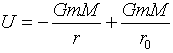 (2)
(2)
です。ここでr0-r=ξとおくと、
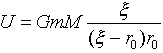 (3)
(3)
となります。ξは質点の落下距離です。
質点mの運動開始からの経過時間は、その運動軌道の線素をdsとして、
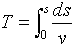 (4)
(4)
で計算できます。ここでsは、運動開始点からmの現在位置までの運動軌道の弧長,vは現在位置での質点mの速度で、v=v(s)という関数関係は必ず成立します。式(4)のdsとvを、最初に導入した(x,y)座標か、極座標(r,θ)で表せば、経過時間Tを最小にする右辺の積分の条件として、ラグランジュ方程式に持ち込めます。
2.線素dsの(r,θ)表現
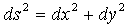 (5)
(5)
ですが、
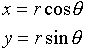 (6)
(6)
に注意すると、
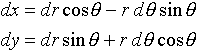 (7)
(7)
なので、
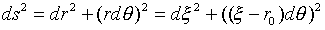 (8)
(8)
が得られます。dr・dθの項が出ないのは、直交曲線座標の一般的性質で、(ξ,θ)が(r,θ)と等価であることは明らかです。
3.速度vの(r,θ)表現
式(3)が、降下することによって質点mが失った、位置エネルギーの減少を表します。エネルギー保存則を仮定し、運動開始点では速度0を仮定すると明らかに、
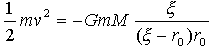
なので、これより、
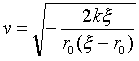 (9)
(9)
です。ただしGM=kとしました。式(9)でξがr0に比べてじゅうぶん小さい場合、分母のξを無視すると、v=(2GMξ/r02)1/2であり、さらにr0が地球の半径と大体等しければ(地表面付近であれば)、GM/r02=gなので、ふつうの最速降下線問題になります。つまり式(9)分母のξは、逆二乗力という条件下では落とせないわけです。式(8),(9)を用いれば、式(4)は、
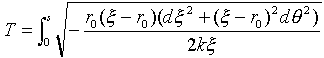 (10)
(10)
と書き換えられます。
4.運動軌道の導入
式(8)と(9)はいうなれば、(x,y)系と(r,θ)系(もしくは(ξ,θ)系)の間に成立する2次元座標系間の一般的関係を導いたにすぎません。しかし質点mは、運動軌道を持つわけですから、ξとθには関数関係ξ=ξ(θ)(r=r(θ))が成り立ちます。どんな関数形かは、これから計算するわけですが。よって式(10)をその意味に捉えるために、ルート内をdθ2で割り、dξ/dθをつくります。もちろん以下の式(11)において、ξはもちろんθの関数と考えます。
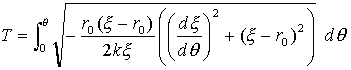 (11)
(11)
次に積分区間は式(10)で[0,s]となっていましたが、式(11)では、積分パラメータがθにおきかわっているので、sとθの関係も考慮します。図-1より、質点mがすべって来た弧長sは、落下距離ξの関数とできそうです。ξはθの関数でした。s=s(ξ)=s(ξ(θ))となり、sもθの関数と仮定します。そうすると積分記号∫の融通性から、[0,s]を[0,θ]に書き換えるだけで済みます。さすがはライプニッツやヨハン・ベルヌーイです。融通が効いて偉い!(ニュートンだとこうはいかない気がする)。あとは式(11)をラグランジュ方程式に載せるだけですが、しんどそうです。
5.ラグランジュ方程式の計算
式(12)がラグランジュ方程式です。
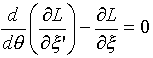 (12)
(12)
上式のLは、用語を流用してラグラジアンと呼びます。またLは、式(11)の積分記号の中身です。
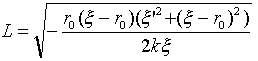 (13)
(13)
ただし、
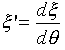
とおいてます。式(13)に式(12)を代入すると、逆二乗力下の最速降下線の微分方程式が、
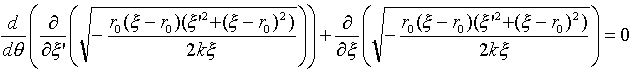 (14)
(14)
と得られますが、ベタな計算をすると、どえらい式になります。
6.近似方程式
式(14)でξ/r0~0を仮定すれば、2.で述べたように、通常の最速降下線になりそうですが、通常のタイプは(x,y)系での微分方程式です。式(14)は、極座標(r,θ)に等価な(ξ,θ)に関するものなので、その影響を調べます。そのために式(14)をr02で割れば、そのラグラジアンは、
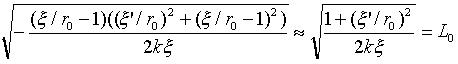 (15)
(15)
となります。L0は、Lの近似ラグラジアンです。一方、通常の最速降下線のラグラジアンは、
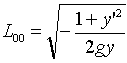 (16)
(16)
と書けます。y'はもちろん、y'=dy/dxのことです。式(16)のルート内に-が現れるのは、例えばNo.1150などとyの方向が逆だからです。式(15)と(16)を比較すると、
y → -ξ,y' → -ξ'/r0,g → k (17)
という対応が成り立ち、重力加速度がgからkに変更された通常の最速降下線になりそうですが、この対応は、実は不完全です。というのは式(16)のy'とはy'=dy/dxのことであり、式(15)のξ'とはξ'=dξ/dθのことなので、(17)の対応が完全に成り立つためには、dx~-r0・dθが必要です。そこで式(7)でr=r0とおき(ξ/r0~0の仮定)、dx=-r0・dθを要求するとθ=π/2が得られ、このときdx=-r0・dθ,dy=dr=-dξとなって(17)が成立します。よって、図-1の運動開始点Aのじゅうぶん近傍(鉛直方向にも,水平方向にも)では、通常の最速降下線で近似できます。逆二乗力は回転対称な力場なので、この結果はA点が地球上空のどこにあっても同じです。
6.局所解
6.ではξ/r0~0の仮定のもとに、通常の最速降下線が得られるためには、dx=-r0・dθが必要でした。それならいっそのこと、χ=-r0θなる座標系に移ってしまったらどうでしょう?。NO.1150とy方向を合わせることにすれば、L00のルート内の-が消え、ξ'=dξ/dχ=-r0-1・dξ/dθのことなので、今度は式(15)と(16)の対応が完全に成り立ちます。
ラグランジュ方程式(12)は、どのような座標系に移っても成り立つ式なので、ξ/r0~0だけの場合(すなわち落下距離がじゅうぶん小さいという仮定のみの場合)にも、(ξ,χ)系では、通常の最速降下線の形が得られることになります。この結果はちょっとびっくりしましたが、(ξ,χ)系とは図-2のような座標系です。
(ξ,χ)に身をおいて考えればわかるように、落下距離がじゅうぶん小さく重力定数を一定とみなせれば、地球中心を向いている逆二乗力は、(ξ,χ)系にとっては、(x,y)系におけるふつうの一様重力場と同じです。よってこれは、逆二乗力が回転対称な場であるという一般的事実から、系に最初から約束されていた解だったのです。ここで極座標を使用したことは、計算技術的には本質的ですが、物理的には本質的ではありません。極座標は、逆二乗力が回転対称な場なので、それに合わせて導入した表現手段にすぎません。それが直交曲線座標だったために、(x,y)系における通常の問題と完全な対応を、たまたま陽に示せたというのは、いってしまえば幸運だったというわけです。
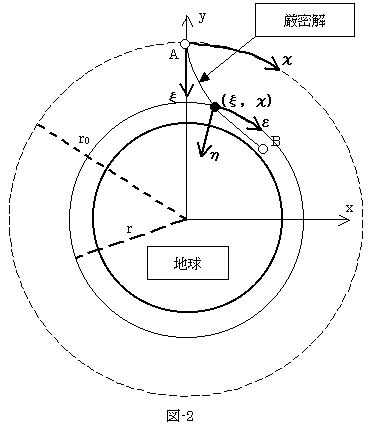
以上の議論は、別に運動開始のA点でなくてもできるはずで、逆二乗力下最速降下線の厳密解の任意の一点で、その局所解は、通常の最速降下線の形で得られます。
局所解が得られれば、それをつなげていくことによって厳密解を、少なくとも数値計算的には得られます。解析的な厳密解はそれの理想化です。局所解の接続を解析的に行う方向で、厳密解の可能性をさぐってみます。
まず局所解を求めます。そのために厳密解の一点(ξ,χ)の近傍に、(ξ,χ)系に平行な(η,ε)系を導入します。(η,ε)系は(ξ,χ)の近傍に限定されるので、(η,ε)では普通の最速降下線問題です。ただ一つ違うのは、質点が点(ξ,χ)で初速度を持つことです。点(ξ,χ)で質点が持つ速度は、式(9)です。(ξ,χ)からさらにη降下した状態を式(9)で想像し、NO.1150を参照しつつ、(η,ε)系での局所解の微分方程式を書くと、
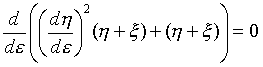 (18)
(18)
となります。εで積分して積分定数をA2、η+ξ=A2sin2(α/2)とおくと、
 (19)
(19)
が得られます。AとBは積分定数で、点(ξ,χ)におけるαの初期値α=uで、(η,ε)=(0,0)という条件から特徴付けられます。これは局所解(19)が、厳密解の一点(ξ,χ)を通るという条件です。
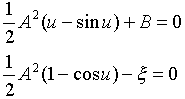 (20)
(20)
より、
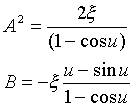 (21)
(21)
これより、
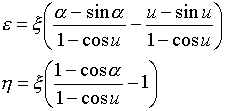 (22)
(22)
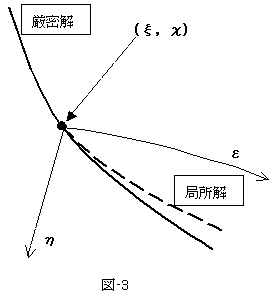
が得られます。積分定数はA,Bと二つあったので、もう一つ条件が必要です(uの決定と同じ)。α → uの極限では、局所解(22)は厳密解と接っしなければなりません。どうしてかというと、厳密解と局所解とが図-3のような関係になっていなければ、局所解をつなげて厳密解を得ることができないからです。式(22)より、
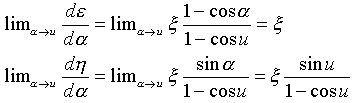
であり、図-3の状態を要求すれば、α → u の極限では、
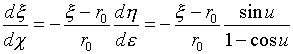 (23)
(23)
が必要です。式(23)では、
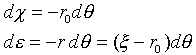
の関係を使っています。BR>
ξ=ξ(χ)=ξ(χ(-r0θ))は、厳密なラグランジュ方程式(14)を満たすものでなければなりません。もしξ=ξ(χ)の関数関係がわかっていれば、式(23)からuを決定できますが、しかしξ=ξ(χ)を求めたいのです。式(23)は厳密解(大域解)とuとの関係を示します。つまりuは、u=u(ξ,χ)であり(η,ε)系の原点(ξ,χ)ごとに違うものだということです。ということは数値積分を行うことだけを考えてみても、大域解と関連付けられたuの決定方程式が必要です。このことは冷静に考えてみれば、実は当然のことです。
厳密なラグランジュ方程式(14)は、2階の微分方程式です。積分定数は二つあり、それは厳密な最速降下線が通過する始点と終点から決まります。これを局所解の始点と終点を決めるAとBまたは、Aとuにおきかえてみれば、局所解の始点と終点は厳密解の二点を通過しなければならないので、ひいては厳密解の始点と終点との関係によって決定され、厳密解(大域解)との関係は避けて通れないことになります。厳密解の微分方程式が必要です。
厳密なラグランジュ方程式(14)は、どえらい式になりそうなので裏返します。何を裏返すのかというと、式(14)では、ξはθの関数と考えていました(これが最も安全です)。しかしθをξの関数と考えてはいけないでしょうか?。
まずうるさく言わなければ、これは常にできます(あなたが、そう思えばいいのです)。次に物理的状況として「最速降下線」なので、ξとθ(またはχ)は、1対1に対応しそうです。とどめとしては、そう仮定して計算して、結果がそれに合えばいいだけの話です。そういうわけで、θをξの関数とみなします。式(10)に戻りましょう。式(10)を再記した式(24)において、θをξの関数とみなします。
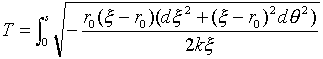 (24)
(24)
θをξの関数の関数とみなしたのだから、ルート内はdξ2で割るべきです。θ'=dθ/dξとして、
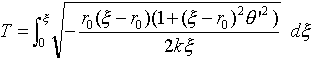 (25)
(25)
となります。ラグラジアンは次式(26)となり、あまり(13)と変わったようにはみえません。
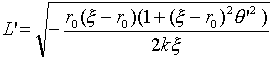 (26)
(26)
しかしラグランジュ方程式をつくると、効果がすぐわかります。ラグランジュ方程式は、どのような変数変換を行おうと成り立つ式でした。式(14)の(ξ,θ)から(θ,ξ)に移ろうとも同じです。
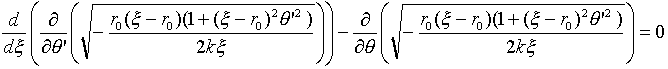 (27)
(27)
式(27)の2項目に注目すると、ラグラジアンはθを陽に含みません。従って、
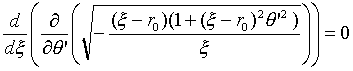
とおけ、Cを積分定数として、
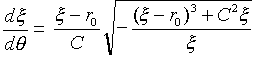 (28)
(28)
となります。ただしC≧0で、図-1より、dξ/dθ≧0としました。
式(28)を微分方程式として積分できれば、ξとθの陽な関係を与えられるはずですが、僕はあきらめました。でもそうなると、数値解を求めるしかありません。そのために、数値積分に便利な大域的な微分方程式を導きます。
8.大域的な数値解
まずχとθの関係は、dχ=-r0dθなので、
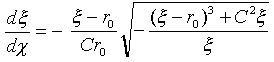 (29)
(29)
です。式(29)を式(23)に使えば、
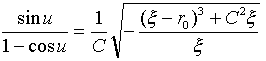 (30)
(30)
が得られます。一方(η,ε)系は一点(ξ,χ)の近傍系なので、式(22)が成立するのは、dα=α-uが小さい範囲に限られます。さらにdε=-r・dθ,dη=dξに注意して、式(22)をαで微分すれば、
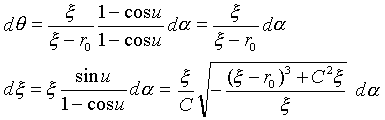 (31)
(31)
が得られます。式(31)の左辺は、厳密解の大域変数の微分(dξ,dθ)であり、右辺のdαの係数も大域変数ξのみで表わされているので、もはやパラメータαは局所解のパラメータとしてではなく、大域的なパラメータと考えて大丈夫です。
よって運動開始点の座標(ξ0,θ0)に、dαが微小として式(31)から決定される(dξ,dθ)を、ひたすら加え続けていけば、厳密解の近似解が得られます。ただし数値解を求めるためには、積分定数を具体的に決める必要があります。積分定数を決めます。式(31)には、積分定数が3個あります。それぞれ、
① 運動開始点の座標に対応するもの.
② 運動終了点の座標に対応するもの.
③ 媒介変数αの初期値に関するもの.
となります。①,③は式(31)の意味から暗黙に要請され、②だけがCとして陽に含まれます。まず③は、αが大域パラメータとなったので任意です。運動開始点でα=0とします。①については図-1を参照し、運動開始点を(ξ0,θ0)=(r0,π/2)とします。②のCについてですが、式(31)のdξ=の右辺のルート内は、常に0以上でなければなりません。かつ位置ξのみの関数です。これは、保存系における広い意味での振動運動を表わす微分方程式に一般的な状況で、式(31)のルート内を0とするξ=ξ1が、運動の回帰点を表わします。どうしてかというと、ξ>ξ1ではルート内が負となるので、ξ=ξ1から運動を続けるためには、ξは減少するほかないからです。実際、ξ=ξ1では式(31)のルート内は0でdξ=0であり、これはξが極値に達したことを示します。よって運動の回帰点ξ1を越えた運動は、系が保存的であることから、ξ≦ξ1で成立した運動を逆向きにたどることになります。すなわち式(28)のルートの符号を決めるときに捨てた、プラス符号の片割れに、解は接続されることになります。以上の状況は、例えば、単振動の微分方程式の第一積分と同じです。そしてθ=θ(ξ)と裏返せると仮定したことは、少なくとも回帰点までは正しかったことが保証されます。回帰点までは正しいので、あとは回帰点で区分して区分的に解をつばげていけば良いこともわかります。
式(31)より、ルート内が0以上となるためには、
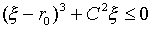 (32)
(32)
が必要です。特定のξ=ξ1で、式(32)の等号を成立させるCを選んだとき、ξ=ξ1が最速降下できる限界降下距離になります。
9.通常の問題との対応
式(31)を詳しく調べれば、きっと通常の最速降下線問題との対応がつくはずです。特に重力定数の変化によって、サイクロイドの転がり半径がどのように変化するのかとかを調べられると思います。でももう、じゅうぶん長いので、またの機会に・・・ということで・・・逃げました。

| NO.1355
| 2003.2.7. | Hkeisuke | 最速降下問題(15)
|
興味深く読ませていただきました。僕なんか勉強不足で局所解を求めることなんて思い浮かびませんでした。最後のほうの式を使って数値解を求めてみようと思います。一応自分のやってみた方法と最終的な目標を書いときます。
僕も、用語を借りると、はじめにラグランジアンを求めて、それからハミルトニアンまで作って作用変数、角変数を使って解こうとしました。(でも途中で断念です・・)
それで目標なんですが、本当はもうひとつ天体があって、3体問題になったときの最速降下線を数値計算でもなんでもいいから見てみたいのです。どこかでスゥイングバイのことが書いてあって、それによると、スゥイングバイをつかって人工衛星を他の惑星まで飛ばすと、普通に行こうとするよりかなり早く行けるというのです。それで、もし最速降下線があったら、それはこのスウィングバイによる軌道を通るのかそれとも単なる通常の最速降下線をつなげたような軌道になるのか。いろいろ関係してきてどうなるのかわかりませんが、もし数値計算して前者のような軌道が現れたら、きっとものすごく感動するだろうなあ・・・ ということで、もしこのことに興味をもった方がいたら何か教えてくださると嬉しいです。(それは解けないよ、とかでも)

 戻る
戻る
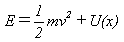 (3)
(3)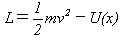 (5)
(5)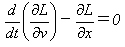 (6)
(6)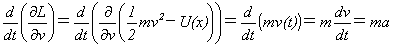 (7)
(7)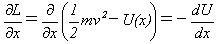 (8)
(8)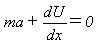 (9)
(9)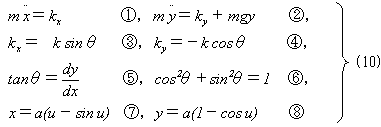
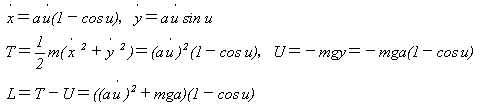
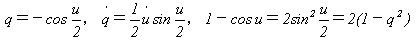
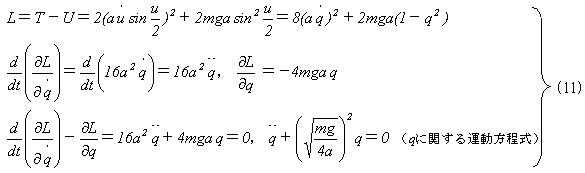
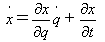 (13)
(13)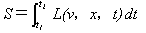 (14)
(14)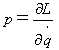 (15)
(15)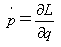 (16)
(16)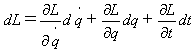 (17)
(17)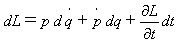 (18)
(18)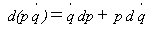 (19)
(19)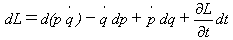 (20)
(20)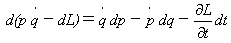 (21)
(21)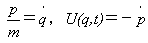 (22)
(22)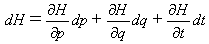 (23)
(23)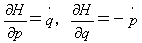 (24)
(24)


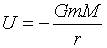 (1)
(1)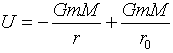 (2)
(2)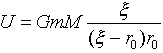 (3)
(3)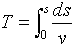 (4)
(4)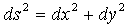 (5)
(5)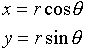 (6)
(6)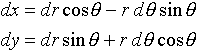 (7)
(7)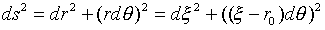 (8)
(8)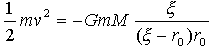
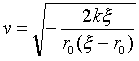 (9)
(9)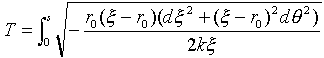 (10)
(10)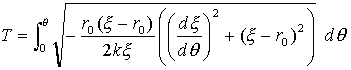 (11)
(11)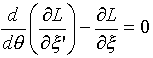 (12)
(12)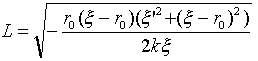 (13)
(13)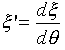
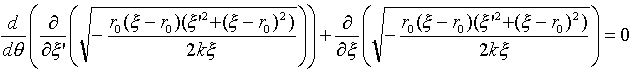 (14)
(14)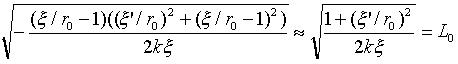 (15)
(15)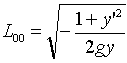 (16)
(16)
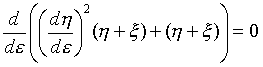 (18)
(18) (19)
(19)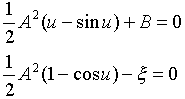 (20)
(20)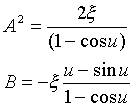 (21)
(21)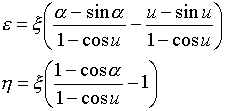 (22)
(22)
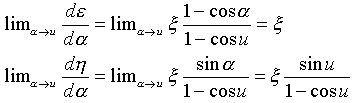
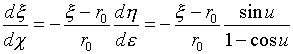 (23)
(23)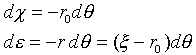
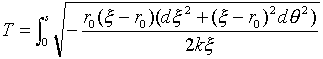 (24)
(24)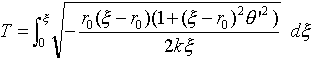 (25)
(25)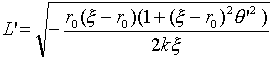 (26)
(26)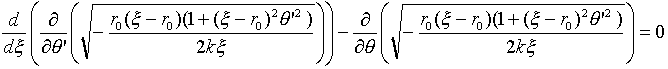 (27)
(27)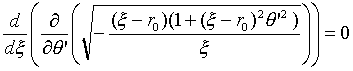
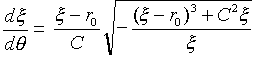 (28)
(28)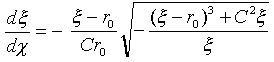 (29)
(29)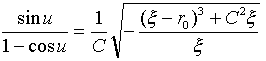 (30)
(30)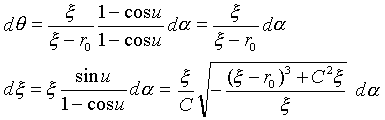 (31)
(31)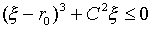 (32)
(32) 戻る
戻る