
Weekend Mathematics/コロキウム室/テーマ別
/19.オイラーの「無限解析入門(1)」3
| NO.553 | '99 6/29 | Junko | オイラーの「無限解析入門(1)」(21) |
NO.544を受けて、
| F(x) | =(1+x)(1+x2)(1+x3)(1+x4)・・・ |
| =1+x+x2+2x3+2x4+3x5+・・・ |

| NO.554 | '99 7/1 | 水の流れ | オイラーの「無限解析入門(1)」(22) |
オイラーの「無限解析入門(1)」第11夜の始まり、始まり。
今度は、ある自然数nを同じものを許す方法で、
自然数の和で表わす方法をC(n)とします。
これは、<水の流れ>にある第19回の応募問題のGの中にでてくる
S(m)と同じ問題です。
そこで、この中にあるT(m、k)の表をm=10まで、
完成しておいてください。素敵な三角形の表になります。
前に、パスカルの三角形、モンモールの三角形と言いましたから、
オイラーの三角形としましょう。 次のようになります。
| m | S(m) | T(m、k) | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1 | 1 | 1 | |||||||||
| 2 | 2 | 1 | 1 | ||||||||
| 3 | 3 | 1 | 1 | 1 | |||||||
| 4 | 5 | 1 | 2 | 1 | 1 | ||||||
| 5 | 7 | 1 | 2 | 2 | 1 | 1 | |||||
| 6 | 11 | 1 | 3 | 3 | 2 | 1 | 1 | ||||
| 7 | 15 | 1 | 3 | 4 | 3 | 2 | 1 | 1 | |||
| 8 | 22 | 1 | 4 | 5 | 5 | 3 | 2 | 1 | 1 | ||
| 9 | 30 | 1 | 4 | 7 | 6 | 5 | 3 | 2 | 1 | 1 | |
| 10 | 42 | 1 | 5 | 8 | 9 | 7 | 5 | 3 | 2 | 1 | 1 |
| f(x)= | (1+x+x2+x3+x4+x5+x6+x7+x8+x9+x10+・・・) |
| (1+x2+x4+x6+x8+x10+・・・) (1+x3+x6+x9+・・・) | |
| (1+x4+x8+・・・) (1+x5+x10+・・・) (1+x6+・・・) | |
| (1+x7+・・・) (1+x8+・・・) (1+x9+・・・) (1+x10+・・・) |

| NO.561 | '99 7/7 | 水の流れ | オイラーの「無限解析入門(1)」(23) |
「オイラーの無限解析入門(1)」第12夜の始まり、始まり。
昨夜、オイラーの三角形を作ってみました。
意味のある数字が並んでいますね。
夜空に輝いている星のように、美しき並んでいます。
このS(m)の数列を並べてみましょう。
1,2,3,5,7,11,15,22,30,42,・・・
何とかして、漸化式みたいのがあれば、計算しやすいのにと、
流れ星の願を賭けていたとき、偶然にも、天使様から、
「理系の数学:5月号」(現代数学社:石谷茂)を読んでみなさいと
お告げがありました。
これを参考しして、書きます。
前夜の母関数を展開した係数がS(m)ですが、
これでは大変な労力です。
そこで、無限等比等比数列の和の公式を用いて、f(x)を簡単にしましょう。
f(x)=1÷(1−x)(1−x2)(1−x3)
(1−x4)(1−x5)(1−x6)
(1−x7)(1−x8)(1−x9)
(1−x10)・・・
この分母を
F(x)=(1−x)(1−x2)(1−x3)
(1−x4)(1−x5)(1−x6)
(1−x7)(1−x8)(1−x9)
(1−x10)・・・
とおいて、 計算してみる方が易しくみえます。
そこで、今夜の宿題です。この計算をしてください。
美しく輝く天の川のように、オイラーの恒等式が見えてきますよ。
お休みなさい。

| NO.581 | '99 7/17 | Junko | オイラーの「無限解析入門(1)」(24) |
f(x)=1÷(1−x)(1−x2)(1−x3)
(1−x4)(1−x5)(1−x6)
(1−x7)(1−x8)(1−x9)
(1−x10)・・・とする。
この分母を
F(x)=(1−x)(1−x2)(1−x3)
(1−x4)(1−x5)(1−x6)
(1−x7)(1−x8)(1−x9)
(1−x10)・・・
とおいて、計算せよというのがNO.561の宿題でした。
これはちょっと大変・・・ということで、「mathematica」の登場です。
F(x)=(1−x)(1−x2)(1−x3)
(1−x4)・・・(1−x30)
=1−x−x2+x5+x7−x12−x15+x22
+x26+x31・・・+x465
x30までの係数は正確なものですから、
F(x)=1−x−x2+x5+x7−x12−x15+x22
+x26+・・・
規則性が見え隠れします。

| NO.582 | '99 7/18 | 水の流れ | オイラーの「無限解析入門(1)」(25) |
オイラーの無限解析入門(1)の第13夜の始まり、始まり。
オイラーの三角形のS(m)の数列を並べてみましょう。
1,2,3,5,7,11,15,22,30,42,・・・
この数列の規則性を見つけるのが目的です。
そのために、母関数を持ち出してきています。
| F(x) | =(1−x)(1−x2)(1−x3) (1−x4)・・・(1−x30) |
| =1−x−x2+x5+x7−x12−x15+x22 +x26−・・・ | |
| =1−x(1+x)+x5(1+x2)−x12(1+x3)+x22 (1+x4)−・・・ |

| NO.584 | '99 7/19 | spooky | オイラーの「無限解析入門(1)」(24) |
さきほど、NO.546を読んだのですが、
2×3×5×7×11×・・・=1/4π2
の証明については、少し疑問が あります。
たしかにオイラーの時代ならよかった(?)のかもしれませんが・・・・。
それは、解析接続に関してです。
たとえば、ζ(s)は確かに複素平面全域に解析接続できます。

詳しいことは私も証明がいまいち理解できていないのでいえませんが、
すこし参考書 を参考に書いてみます。

だから、1+2+3+4+・・・・の和というのは、
実際には収束しないのですが、 これがζ(-1)であると考えると、
上の式より値が出てきてしまうのです。
しかし、ζ(−1)というのはすべての自然数の和とは違うわけです。
昔はこのような区別が付いていなかったため、
オイラーはこのように書いたのでしょう。
つまり、すべての自然数の積というのも、
Γ(s)のs→∞の極限とかそういうもの なのかもしれません。
ただ、それがすべての自然数の積であるとは思わない方がいいと思います。
あくまでも、関数の解析接続したものを考えているわけですから。
Γ関数がいくら階乗の拡張だといっても、Γ(1/2)=(−1/2)!
とは考えないでしょう??
いわゆるオイラーの公式も実関数の立場(オイラーの立場)では
テイラー展開に複素数を代入するという、無茶な代入をしなければなりません。
本来ならば、複素関数として3つを定義して考えなければならないわけです。
ということは、もともと、1×2×3×4・・・・という式は何らかの関数の
解析接続であるはずで、
その式を元にしてあのような証明をたてるのはかなり疑問だと思うのですが・・・。
どうでしょうか??
まあ、題名に「オイラーの」とついていたので、
オイラー時代の考えでともできるの ですが、 どうなんでしょうね??

| NO.586 | '99 7/20 | Junko | オイラーの「無限解析入門(1)」(27) |
α(1)=1,α(2)=5,α(3)=12,α(4)=22,・・・の一般項を求めてみます。
この数列の階差数列(隣同士の差をとって作った数列)をβ(n)とします。
β(1)=4,β(2)=7,β(3)=10,・・・となり、
これは初項4、公差3の等差数列になっています。
従ってβ(n)=4+3(n−1)=3n+1
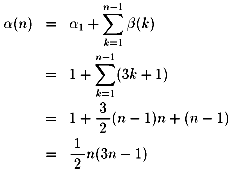

| NO.588 | '99 7/20 | オイラーの「無限解析入門(1)」(28) |
オイラーの無限解析入門(1)の第14夜の始まり、始まり。
皆さんは、次の数列の名前をご存じでしょう。
三角数 1,3,6,10,15,21,28、36、・・・
四角数 1,4,9,16,25,36,・・・
五角数 1,5,12,22,35,51,・・・
13夜の数列がこの五角数なのです。
さて、歴史的なことを書きます。
1740年にフランス系のベルリンの数学者ノデがオイラーに手紙を書いて、
与えられた整数nが幾通りの方法でk個の異なる整数の和として表されるかを問うて来た。
(ここで、扱っている記号ではA(n)のことです。)
オイラーは直ちにといっていいくらいに返事をした。
次いで、2,3ヶ月もせぬうちに、ペテルスブルク・アカデミーに論文を提出した。
彼は後に数度にわたりこの問題に立ち戻ることになった。
1748年の「無限解析入門(1)」にいくらか詳しく、この問題を扱っており、
また最後に扱ったのは1768年のことであった。
ノデの問題に対するキーは次の無限積が無限級数へ展開されることが彼の心を打ったのは
言うもでもない。
零でない係数がどれも±1であるということばかりでなく、
指数が容易に分かるように「五角数」n(3n−1)/2である。
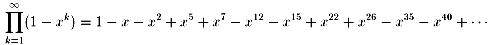
(これが、オイラーの五角数定理、または、オイラーの恒等式という。)
1750年、オイラーはほぼ10年を要して、この証明をゴールドバッハに送ることができた。
ヤコービが見いだしたように、正確な証明はテータ関数や保型形式の理論を待たねばならない。
<以上までの参考文献:数論(アンドレ・ヴェイユ;足立恒雄訳)「日本評論社」>
また、この公式のことを数学セミナー3月号の載っている静岡大学の浅井哲也先生は
「数論に現れるいくつかの不思議な等式に魅力を引かれるようになりました。
僕にとっての数学の女神さまは、多少象徴的な言い方になりますが、例えば、この五角数定理でした。」
とね。
これで、本題にもどります。
| f(x) | =(1+x+x2+x3+x4+x5+x6+x7+x8+x9+x10+・・・) |
| (1+x2+x4+x6+x8+x10+・・・) (1+x3+x6+x9+・・・) | |
| (1+x4+x8+・・・) (1+x5+x10+・・・) (1+x6+・・・) | |
| (1+x7+・・・) (1+x8+・・・) (1+x9+・・・) (1+x10+・・・) | |
| =s(0)+s(1)x+s(2)x2+・・・+s(m)xm+・・・・ |
ここで、今夜の宿題です。
左辺のxmの係数は0に等しいですから、
ここから、s(m)を求める関係式を発見してください。
今夜は長くなりましたが、徐々にオイラーの域に近づくことができました。
みなさん、お休みなさい。

| NO.611 | '99 9/13 | 月の光 | オイラーの「無限解析入門(1)」(29) |
NO.540 オイラーの「無限解析入門(1)」(16)にある
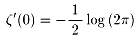 を示せ、について
を示せ、について
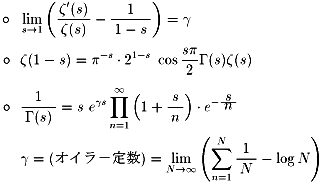
を用いて証明してください。

| NO.615 | '99 9/27 | 水の流れ | オイラーの「無限解析入門(1)」(30) |
オイラーの無限解析入門(1)の第15夜の始まり、始まり。
皆さん!お久しぶりです。9月24日の中秋の名月を鑑賞されましたか。
いつ見ても、夜空に輝く美しい満月はいいですね。宇宙への夢を奏でてくれます。
さて、NO.542の第9夜の話をご存じですか。
もう一度、書きます。
オイラーは1740年の秋に、フランスの数学者フィリップ・ノードから、
「自然数を異なる自然数の和として表わす方法がいくるあるか?」という手紙を受け取りました。
これが、オイラーの興味を引きました。少し説明します。
例えば、n=6のとき、異なる自然数の和として、次の4通りがあります。
6,5+1、4+2,3+2+1 です。
6を構成している数字は1回だけしか使えません。
だから、異なっている数字なら、数字はいくつ使ってもよいです。
ここで、ある自然数nを異なる自然数の和で表わす方法をA(n)とします。
つまり、A(6)=4 です。
次に、6を構成している数字が奇数だけになっている方法を考えて見ます。
5+1,3+3,3+1+1+1,1+1+1+1+1+1
の4通りです。
奇数という制限はありますが、同じ数字を繰り返して使ってもよいです。
ある自然数を奇数の和で表す方法をB(n)とすれば、
B(6)=4となります。
皆さん、A(6)=4 、B(6)=4 が偶然でしょうか。
そして、NO.544の第10夜を見て下さい。
当然ある関数の係数として表れてきます。これが、母関数です。
そこで、皆さん、次の関数を展開してくださいね。
当然係数に注目ください。
そして、この係数がどうして、数列{A(n)}なのかも考えてください。
| F(x) | =(1+x)(1+x2)(1+x3)(1+x4)・・・・・・ |
| =1+x+x2+2x3+2x4+3x5 +4x6+5x7+6x8+8x9+10x10 +12x11+15x12+・・・・・・ |
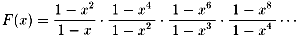
1−xn はnが偶数のものは約分されて消えて、nが奇数のものだけが分母に残ります。
よって、
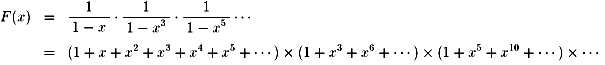
この式の持っている意味を説明します。
ここから、、「数学の宇宙」<現代数学社>のオイラーの91ページから引用します。
例えば、x5の係数は x5、x3・x2、x5から得られます。
だから、xnの項の数と、指数がすべて奇数ですから奇数の和として
x と書き方法は同じです。
言い換えればこのことは、異なる自然数の和で表わす方法をA(n)と
奇数の和で表す方法をB(n)は正確に等しいことを示しています。
これが、オイラーが見つけた証明です。
自然数を分解することについて、微妙で曖昧だった真実を明確にしたこの論証は、
まさに傑作といわねばなりません。
そしてこれは、次のようなオイラー数学の典型的な正確を表しています。
1.オイラーは抽象的な記号を用いた式の扱いが素晴らしく巧みでした。 その能力はこの証明にもはっきり現れています。 よって彼は”どんな場合にも、最も偉大な記号の使い手”という評判を得ています。
2.オイラーの最も実り豊かな数学的戦略の1つは、同じ式を二種類の方法で書き表すことで、
その二つの式を等式化することによって力強い結論を引き出していくものです。
これがまさにその通りです。
また、読者の皆さんは、既に、「ゼーター関数ζ(2)物語」のときにも、
どこまでも異なる二つの見地から1つの目標を見出していく美しい論証で、
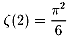 を発見したことも良い例です。
を発見したことも良い例です。
3.彼の代数学に高度な操作や技術的に優れた技量を取ってみたとき、
そこに残るのは創意工夫の力です。これはもうただただ驚くほかありません。
この章の最後に、こんなことばが書いてありました。
『誰よりも洞察力にあふれ、 誰よりも影響力をもち、 誰よりも創造性豊かな数学者! それはスイスのレオナルド・オイラー!』

 戻る
戻る