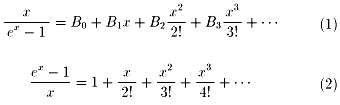
この2式を掛けると、明らかに右辺は1になります。
そして、当然 B0=1 であり、xnの係数は 0 です。
これを左辺で見ますと、
Weekend Mathematics/コロキウム室/テーマ別
/19.オイラーの「無限解析入門(1)」2
| NO.489 | '99 5/23 | 水の流れ | オイラーの「無限解析入門(1)」(11) |
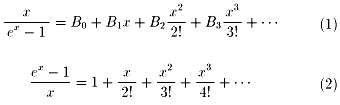
この2式を掛けると、明らかに右辺は1になります。
そして、当然 B0=1 であり、xnの係数は 0 です。
これを左辺で見ますと、
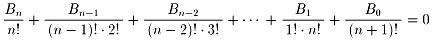
両辺に(n+1)! を掛けて 、2項係数で表すと
n+1C1Bn+
n+1C2Bn−1+
n+1C3Bn−2+
・・・+
n+1CnB1+
n+1Cn+1B0=0
これは n+1 のところを n で書き直し、さらに組合せの性質もつかって、
nCn−1Bn−1+
nCn−2Bn−2+
・・・+
nC2B2+
nC1B1+
nC0B0=0
これは(B+1)n−Bn=0 と書けば分かり易いです。
ただし、展開後の B の指数を下の添え字にしてください。
ここで、n=2 を代入して 2B1+1=0 ∴B1=−1/2
n=3 を代入して 3B2+3B1+1=0 ∴B2=1/6
n=4 を代入して 4B3+6B2+4B1+1=0 ∴B3=0
n=5 を代入して 5B4+10B3+10B2+5B1+1=0 ∴B4=−1/30
後は、読者に任せます。分かったことは
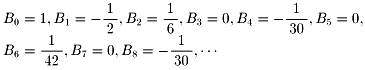
(B1以外の奇数番号のBnは0になっています)
ここで、ゼーターの値 ζ(0)=−1/2,ζ(−1)=−1/12,ζ(−2)=0, ζ(−3)=1/120,・・・を比較してください。 すると、
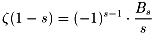
と簡単に書けることをオイラーは1749年に発見しました。
さて、ζ(2),ζ(3),ζ(4),・・・とB2、B3,B4,
・・・の関係については、オイラーは
すでに1735年に見つけていました。
ここの関係を発見するにはガンマ関数Γ(s)の登場になります。
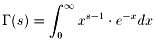
と書きます。
ここで、やっと、今夜の宿題です。
このガンマ関数Γ(s)の下記の性質を示してください。
(1) Γ(s+1)=sΓ(s) 、Γ(1)=1
(2) Γ(s+1)=s!
この先の展開に不安を持ちつつ、第6夜はゆっくりねましょう

| NO.496 | '99 5/26 | Junko | オイラーの「無限解析入門(1)」(12) |
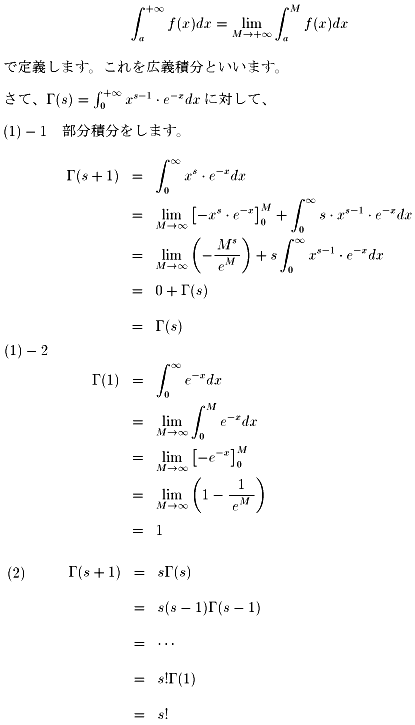

| NO.506 | '99 6/1 | 水の流れ | オイラーの「無限解析入門(1)」(13) |
オイラーの「無限解析入門(1)」の第7夜の始まり、始まり。
前夜、ガンマ関数Γ(s)の話をしましたね。
もう一度、書いておきます。
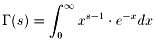
を言います。
さて、いきなりですが、今夜の宿題です。
次の関数が、ゼーター関数ζ(s)の積分における表現になっていること
を示してください。
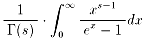
皆さん、この積分をしてみてください。今夜は短いお話でした。

| NO.509 | '99 6/3 | 月の光 | オイラーの「無限解析入門(1)」(14) |


| NO.538 | '99 6/19 | 水の流れ | オイラーの「無限解析入門(1)」(15) |
リ−マンのゼ−タ関数は、積分によっても次のように表現できます。
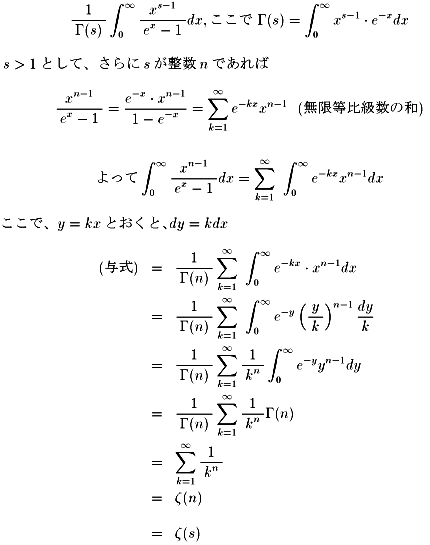
「素数の不思議:好田順治著(現代数学社)」に載っていましたので、紹介します。

| NO.540 | '99 6/21 | 水の流れ | オイラーの「無限解析入門(1)」(16) |
オイラーの「無限解析入門(1)」第8夜の始まり、始まり。
自然数全体の和はオイラーが1749年にゼーター関数を用いて、
奇妙な計算結果を導きました。
1+2+3+4+・・・=−1/12
そして、自然数の積はリーマンが1859年にゼーター関数を用いて、
次のような奇妙な計算結果を導きました。
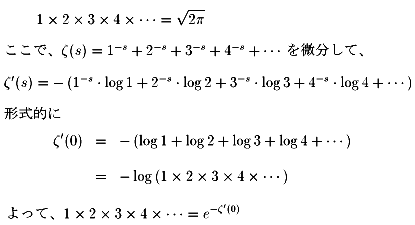
そこで、今夜の宿題です。
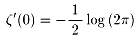 を示してください。
を示してください。

| NO.542 | '99 6/23 | 水の流れ | オイラーの「無限解析入門(1)」(17) |
オイラーの「無限解析入門(1)」第9夜の始まり、始まり。
今夜は「数学の宇宙(現代数学者:中村由子訳)」を読んで、
多くの引用をさせてもらいながら、お話をします。
オイラーは1740年の秋に、フランスの数学者フィリップ・ノードから、
「自然数を異なる自然数の和として表わす方法がいくるあるか?」
という手紙を受け取りました。これが、オイラーの興味を引きました。
数日後、彼は「ここ数週間苦しめられた視力の低下のせいで返事の遅れた」
ことを詫びる手紙を添えて解答を送りました。
解答の紹介は後にしまして、少し説明します。
例えば、n=6のとき、異なる自然数の和として、次の4通りがあります。
6,5+1、4+2,3+2+1 です。
6を構成している数字は1回だけしか使えません。
だから、異なっている数字なら、数字はいくつ使ってもよいです。
ここで、ある自然数nを異なる自然数の和で表わす方法をA(n)とします。
つまり、A(6)=4 です。
次に、6を構成している数字が奇数だけになっている方法を考えて見ます。
5+1,3+3,3+1+1+1,1+1+1+1+1
の4通りです。奇数という制限はありますが、
同じ数字を繰り返して使ってもよいです。
ある自然数を奇数の和で表す方法をB(n)とすれば、
B(6)=4となります。
皆さん、A(6)=4 、B(6)=4 が偶然に一致したかどうか、
これから、2,3調べてください。
これが今夜の宿題です。
n=7,8,・・・を調べてください。

| NO.543 | '99 6/26 | Junko | オイラーの「無限解析入門(1)」(18) |

| NO.544 | '99 6/27 | 水の流れ | オイラーの「無限解析入門(1)」(19) |
オイラーの「無限解析入門(1)」第10夜の始まり、始まり。
昨晩、ある自然数nを異なる自然数の和で表わす方法をA(n)として、
2,3調べてくださいと、言って床につきましたが、
この数列はいちいち計算しなければならないのでしょうか?
いえいえ、当然ある関数の係数として表れてきます。これが、母関数です。
そこで、皆さん、今夜の宿題です。
次の関数を展開してくださいね。
当然係数に注目ください。
そして、この係数がどうして、数列{A(n)}なのかも考えてください。
F(x)=(1+x)(1+x2)(1+x3)(1+x4)・・・・・・

| NO.546 | '99 6/27 | 月の光 | オイラーの「無限解析入門(1)」(20) |
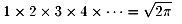
この式は初めて見たので驚きました。
早速証明に取り掛かりましたがまだ出来ていません。
そのかわりこの式を仮定して別の奇妙な式が得られました。
2×3×5×7×11×・・・=1/4π2
左辺は素数の無限積です。
証明)
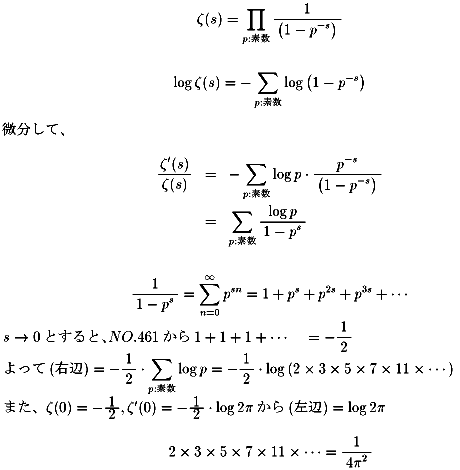
証明終)

 戻る
戻る