
Weekend Mathematics/コロキウム室/テーマ別
/15.ゼーター関数物語2
NO.374 '99 3/1 水の流れ ゼーター関数物語(21)
ゼーター関数物語ζ(2)物語第7夜の始まり、はじまり。
昨夜の無限級数と無限席が等しいことが分かったでしょうか。
コロキウム室を愛好している皆さんにはちょっと、
首をひねっただけで解けただろうと思います。
さて、レオナルド・オイラーは広範囲に業績を残した
18世紀を代表する数学者であります。
彼は、生涯に45冊の本と700編以上の論文を書いています。
研究範囲は、フェルマーの定理のn=3,4の場合の証明などの整数論から、
幾何学、代数学、微分積分学、確率論、
さらには、現代のトポロジーやグラフ理論の誕生につながる問題、
力学や音楽理論や造船学にまで及んでいる。
さらに、彼は、新しい記号メーカーでもあった。
一例を挙げると、関数記号f(x)、指数関数の底e
(これなど、自分のEulerの頭文字をとっている)、
円周率π(先駆者はいたが・・・)、
虚数単位のi、和の記号Σなど特殊な記号を導入している。
また、三角関数の定義を比例であるかのように、
一般的なものとして普及させることに成功している。
これらの一部は、1748年に発表された『無限小解析入門』
の中に書いてあります。
後に、かの数学者ガウスは、初めてオイラーの業績に出会ったときのことを回想し、
『それまで味わったことのない熱い思いがわきあがってきた。』と言い、
さらに、『広い科学分野の限界にまで挑戦してやろうと固く決心した。』と書いています。
<以上のまでの原稿を書くにあたっての参考文献を挙げておきます。>
オイラーがセントペテルスブルグ大学での初年度、
1734年に発表したのがゼーター関数
ζ(2)=1+1/4+1/9+1/16+・・・の値でした。
このとき、彼はこう語っています。
・・・私は予想もしなかったエレガントな式を発見した。
・・・それもπを用いてのものである。
このエレガントな式から結論を導き出すために、
オイラーには2つの道具が必要でした。
1つは初歩の三角法のいわゆる“正弦関数sinx”です。
ここで、f(x)=sinx のグラフを書いてください。
ここがオイラーの洞察の核心があるのです。
グラフがちょうどx軸と交わるときのxの値に対して関数の値は
0であることを思い出してください。
x=0,±π,±2π,±3π,±4π,・・・,これらの値のとき、
sinx=0になります。
さて、今夜の問題です。
解析学でテイラー級数の展開を学んだ人なら即座に分かります。
次の関数をx=0でテイラー展開または、
マクローリン(1698〜1746)展開してください。

NO.376 '99 3/1 Junko ゼーター関数物語(22)


NO.377 '99 3/2 月の光 ゼーター関数物語(23)
NO.374のテ−ラ−展開です。
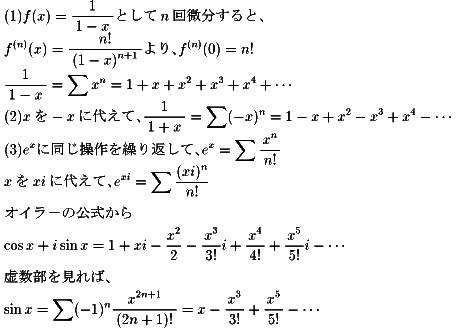

NO.378 '99 3/2 Junko ゼーター関数物語(24)
NO.374の(3)のテ−ラ−展開です。


NO.379 '99 3/3 水の流れ ゼーター関数物語(25)
ゼーター関数ζ(2)物語第8夜の始まり、始まり。
オイラーは当然ζ(2)=1+1/4+1/9+1/16+・・・の問題ことは
師であるヨハンを通じて聞き及んでいたことでしょう。
最初は彼も、いずれ正確な値が出てくるだろうと期待して
この級数の項を単に延々と足して
いってみたと述べています。
結局、小数点以下20位までの和を出してみて
(コンピューターなどがなかった時代ですから、並々ならぬ計算作業です)、
それが、1.6449・・・という数値になっていきそうだと分かりましたが、
残念ながらこの数字ではどうにも落ち着きが得られなかったのです。
あきらめることなく彼は問題に取り組み続け、ついに謎の
扉を開く鍵を発見したのです。
その1つの鍵が第7夜で述べた、正弦関数
のテイラー級数の展開でした。
sin x=x−x3/3!+x5/5!−x7/7!+x9/9!−・・・
ここで、重要なのはオイラーが“無限に続く多項式”として
sin x を代表させていることです。
これがオイラーが謎を解くのに必要な有効な手段の1つになりました。
もう1つの鍵は三角法でも微分でもない単純な代数でした。
sin x のテイラー展開が終わりのない多項式を示唆したわけですから、
オイラーは有限な多項式によくある性質を調べてみることにして、
そこから無限のケースへと大胆に拡大していくことにしました。
さて、ここで今夜の問題です。
『次の条件を満たすn次の多項式P(x)を見つけなさい。
P(0)=1、P(a1)=0,P(a2)=0,
P(a3)=0,・・・,P(an)=0』
今日は雛祭り。
また、夕方西の空には下から順に、水星、木星、金星、土星と
ほとんど一直線上に並びます。
オイラーは晩年孫と遊んだり、天王星に関する
最新の理論について話し合ったりして過ごしたりしたと言われます。
きっと、これらの惑星は今も昔も変わらず、
地球とともに太陽の周りを公転していることでしょう。お休みなさい。」

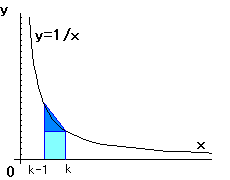
NO.380 '99 3/3 月の光 ゼーター関数物語(26)
NO.357の(2)についてです。
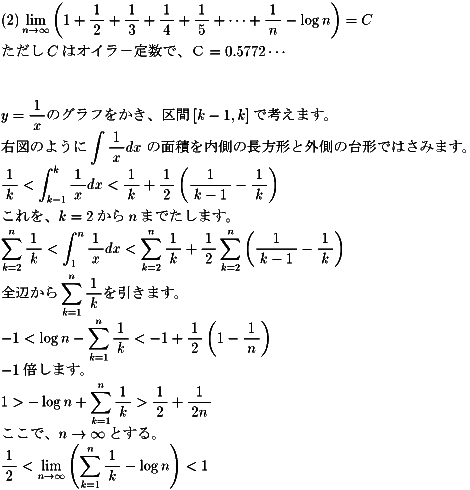
|  |

NO.384 '99 3/5 月の光 ゼーター関数物語(27)
NO.379の
『次の条件を満たすn次の多項式P(x)を見つけなさい。
P(0)=1、P(a1)=0,P(a2)=0,
P(a3)=0,・・・,P(an)=0』に対する答えです。
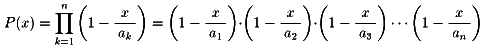

NO.385 '99 3/6 月の光 ゼーター関数物語(28)
NO.357の(2)についてです。


NO.387 '99 3/7 ゼーター関数物語(29)
ゼーター関数ζ(2)物語第9夜の始まり、始まり。
ゼーター関数ζ(2)物語第6夜の始まりに、こんなことをかきましたね。
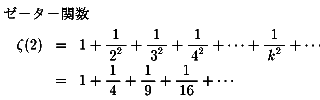
の値を追い求めていたベルヌーイ兄弟にはその和の正確
な値を出すことはできませんでした。
ヤコブは”今もって私たちの必死の探求の目をかいくぐっている、
その答えを教えてくれる人があるならば、私たちは多いに感謝する・・・”
と言い訳をしています。
ベルヌーイ兄弟は何もアイデアももっていませんでした。
ところが、『解決!フェルマーの最終定理<現代数論の軌跡>』
を読んでみると、1728年に
ベルヌーイは、この和が8/5に近いと述べたり、
1729年にゴールドバッハはこの和が1.6437と
1.6453の間にあることを言ったり、
オイラーは1731年に1.644934・・・であることをつきとめ、
結局、小数点以下20位までの和を出してみて
(コンピューターなどがなかった時代ですから、並々ならぬ計算作業です)、
それが、1.64493406684822643647・・・という数値になっていきそうだと分かりました。
そして、オイラーは「私は何度試みても、それらの和に対する近似値しか得られませんでした・・
・しかるの、まったく思いもかけず、
ζ(2)の優雅な公式を発見できました。
円周率πに関係しているのです」とその喜びを書いています。
(注:ここまで、『解決!フェルマーの最終定理<現代数論の軌跡>』を引用しました)
さて、ゼーター関数ζ(2)物語第8夜の下の問題を思い出してください。
『次の条件を満たすn次の多項式P(x)を見つけなさい。
P(0)=1、P(a1)=0,P(a2)=0,
P(a3)=0,・・・,P(an)=0』
この答えを「月の光」さんによって、解決しました。
NO.384参照ください。

無限の積と無限の和が等しくなったのですからこれ以上はない意外な結果です。 オイラーのような洞察力を持った数学者にとって、 これはおおいに示唆に富むものでした。 もう、無限の積を展開して、x2の係数を比べればよいのです。
最後の結果は読者に任せるとして、
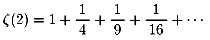
の値こそ何十年もの間数学者たちの追求を逃れ続けた値です。
それをレオナルド・オイラーは独特な方法で
ついにゼーターζ(2)の値を発見しました。
後に、ドイツの数学者リーマン(1826〜1866)によって、
次のように拡張されました。
皆さんは、リーマン積分等でご存じでしょう。
リーマン・ゼーター関数ζ(s)とは
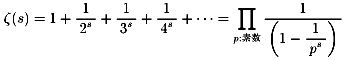
さて、今夜の問題です。
皆さんもオイラーと同じようにこの驚くべき和ζ(2)を
求めてください。この後に、次の値も工夫して求めてください。
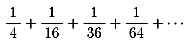

NO.390 '99 3/9 月の光 ゼーター関数物語(30)


NO.391 '99 3/10 月の光 ゼーター関数物語(31)
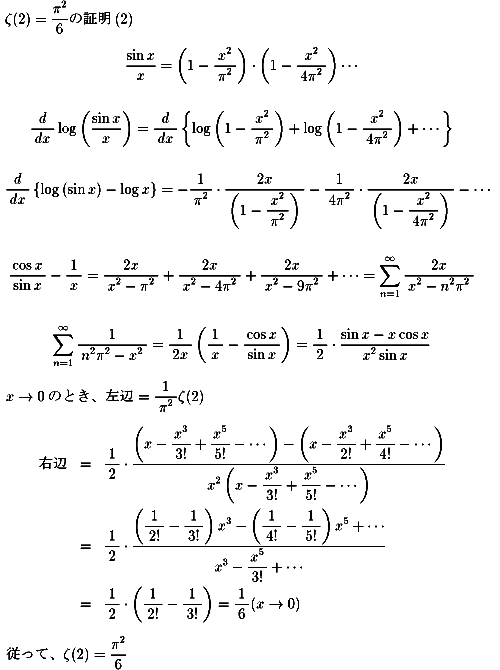

NO.392 '99 3/10 月の光 ゼーター関数物語(32)
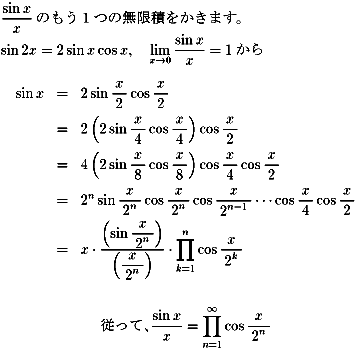

NO.394 '99 3/11 月の光 ゼーター関数物語(33)

| 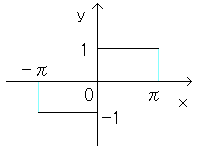
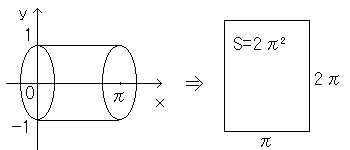 |
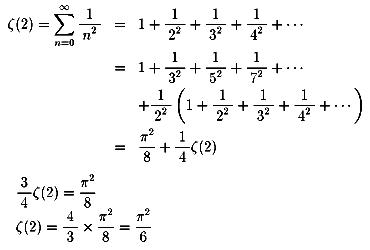


NO.396 '99 3/12 Junko ゼーター関数物語(34)
NO.394においては、
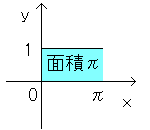
0<x<πにおける関数f(x)の回転体の表面積から導いています。
x=0,x=π,x軸,y=f(x)で囲まれた部分の面積からも導き出せます。
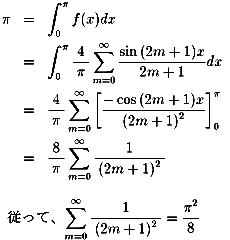

NO.398 '99 3/12 月の光 ゼーター関数物語(35)
NO.387
ゼーター関数物語第9夜の問題に対する答えです。
NO.394の中で示したように、
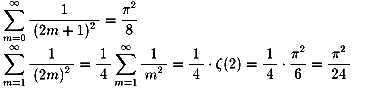

NO.401 '99 3/13 月の光 ゼーター関数物語(36)
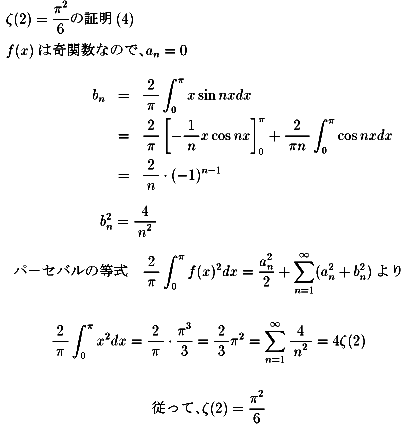

NO.403 '99 3/14 水の流れ ゼーター関数物語(37)
ゼーター関数ζ(2)物語第10夜の始まりです。
さて、昨夜次のような問題を出したところ、
「月の光」さんや「Junko」によって、
それぞれ、エレガントでかつユニークな解法で値を求められました。
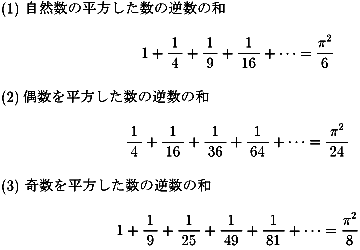
皆さんも、これらの値を覚えておかれるといいでしょう。
レオンハルト・オイラーはこれでもう十分に満足してこの素晴らしい栄光の上に
どっかりとあぐらをかいていませんでした。
価値あることなら何事も徹底的に掘り下げていくという才能が彼の数学の特徴です。
かの素晴らしい“和”の場合も、彼にしてみればまだ表面を引っ掻いただけに過ぎませんでした。
オイラーは自らがキ−となる式をもう一度思い出してください。

オイラーは偶然にも、イギリス人のジョン・ウォリス(1616〜1703)に
よって発見されたπの近似式と同じ結果を
彼独自のユニークな方法で得ています。
それでは、今夜の問題です。
ジョン・ウォリスの公式をオイラー風に求めてください。
次の夜に、ζ(4)、ζ(6)、ζ(8)を求めますが、予習をお願いします。
一般に、対称式は基本対称式の整式として表されます。
問題

NO.407 '99 3/16 Junko ゼーター関数物語(38)
NO.403の宿題の答えです。
a2+b2=(a+b)2−2ab=s12−2s2
展開公式 (a+b+c)2=a2+b2+c2+2ab+2bc+2ca (a+b+c)(a2+b2+c2−ab−bc−ca)=a3+b3+c3−3abcを使って、 a3+b3+c3=s13−3s1s2+3s3
a4+b4+c4+d4=s14−4s12s2+2s22+4s1s3−4s4

NO.409 '99 3/17 水の流れ ゼーター関数物語(39)
a4+b4+c4+d4は
4次の同次式ですから、基本対称式の整式に表されることより、与式は次のようになります。
s1は1次式、s2は2次式、
s3は3次式、s4は4次式に注目していくと、
与式=s14+As12s2+Bs22+Cs1s3+Ds4
と表されます。
ここで、両辺のa,b,c,dに4組の意味のある数値を代入して、
A,B,C,Dの4元方程式を作って、解きます。
ちなみに、(a,b,c,d)=(1,1,0,0)、(1,1,1,0)、(1,
1,1,1)、
(1,−1,1,−1)を代入して、
2=16+4A+B
3=81+27A+9B+3C
4=256+96A+36B+16C+D
4=4B+D
これを解いて、正解に至ります。

NO.410 '99 3/17 水の流れ ゼーター関数物語(40)
(一部記述にあやまりがありました。ごめんなさい。訂正junko3/18)
ゼーター関数ζ(2)物語第11夜の始まり、始まり。
昨夜の予習問題は、次のように基本対称式で表されます。
NO.407をご覧ください。
a4+b4+c4+d4=s14−4s12s2+2s22+4s1s3−4s4
そこで、オイラーの自らが発見したキ−となる式をもう一度思い出してください。

したがって、今夜の宿題です。
これを利用して、ζ(2)、ζ(4)、ζ(6)、ζ(8)まで、求めてください。
この続きは明日の夜お話しましょう。
オイラーはパソコンのない時代にζ(26)までよく手ですごい計算をしたものだと驚きます。

 戻る
戻る