Weekend Mathematics／コロキウム室／テーマ別 ／13.互いに素



コロキウム室(互いに素)


NO.260 　　　 '99 1/5 　　月の光 　　　 互いに素（１）

任意に自然数を２つ選ぶ時、それらが互いに素である確率を求めよ。



NO.263 　　　 '99 1/6 　　水の流れ 　　　 互いに素（２）

自然数Ｎ＝ａαｂβｃγ・・・ （素因数分解した形）とおくと、
Ｎと互いに素（１以外に公約数をもたない）なものの個数をψ（Ｎ）と表す （オイラー関数）。






NO.269 　　　 '99 1/10 　　　豊作 　　　 互いに素（３）



＊このTeXファイルもご本人の提供です。




NO.270 　　　 '99 1/10 　　　水の流れ 　　　 互いに素（４）

自然数Ｎ＝ａαｂβｃγ・・・（素因数分解した形）とおくと、
Ｎと互いに素（１以外に公約数をもたない）なものの個数をψ（Ｎ）と表す
（オイラー関数）。
ψ（Ｎ）＝Ｎ(１−1/a)(１−1/b)(１−1/c)・・・・・・　となる。

ここで、このオイラー関数の簡単な性質を書きます。

定理１．ＮとＭが互いに素なら、ψ（ＮＭ）＝ψ（Ｎ）・ψ（Ｍ）

定理２．Ｎ＝ａαのとき、（ａは素数）
ψ（ａα）＝ａα−ａα−１＝ａα（１−1/a）
だから、これと定理１から
ψ（Ｎ）＝Ｎ(１−1/a)(１−1/b)(１−1/c)・・・・・・　

定理３．各素因数ａに対して、

　ψ（１）＋ψ（ａ）＋ψ（ａ２）＋・・・＋ψ（ａα）
＝１＋（ａ−１）＋（ａ２−ａ）＋・・・＋ａα（１−１／ａ）＝ａα

例　Ｎ＝１６＝２４のとき、

　ψ（１）＋ψ（２）＋ψ（４）＋ψ（８））＋ψ（１６）　
＝１＋１＋２＋４＋８
＝１６

定理４．Ｎのすべての約数を１，ｐ，ｑ，ｒ，・・・，Ｎとすると、
ψ（１）＋ψ（ｐ）＋ψ（ｑ）＋ψ（ｒ）＋・・・＋ψ（Ｎ）＝Ｎ

例　Ｎ＝１５のとき、１５とすべての約数は１，３，５，１５だから

　ψ（１）＋ψ（３）＋ψ（５）＋ψ（１５）
＝１＋２＋４＋８
＝１５

そこで、問題です。
ψ（Ｎ）＝６　となる自然数Ｎを求めよ。＜参考：オイラー関数表参照＞

オイラー関数表
Ｎψ(Ｎ)Ｎψ(Ｎ)Ｎψ(Ｎ)Ｎψ(Ｎ)Ｎψ(Ｎ)
　　１　　１　２１　１２　４１　４０　６１　６０　８１　５４
　　２　　１　２２　１０　４２　１２　６２　３０　８２　４０
　　３　　２　２３　２２　４３　４２　６３　３６　８３　８２
　　４　　２　２４　　８　４４　２０　６４　３２　８４　２４
　　５　　４　２５　２０　４５　２４　６５　４８　８５　６４
　　６　　２　２６　１２　４６　２２　６６　２０　８６　４２
　　７　　６　２７　１８　４７　４６　６７　６６　８７　５６
　　８　　４　２８　１２　４８　１６　６８　３２　８８　４０
　　９　　６　２９　２８　４９　４２　６９　４４　８９　８８
　１０　　４　３０　　８　５０　２０　７０　２４　９０　２４
　１１　１０　３１　３０　５１　３２　７１　７０　９１　７２
　１２　　４　３２　１６　５２　２４　７２　２４　９２　４４
　１３　１２　３３　２０　５３　５２　７３　７２　９３　６０
　１４　　６　３４　１６　５４　１８　７４　３６　９４　４６
　１５　　８　３５　２４　５５　４０　７５　４０　９５　７２
　１６　　８　３６　１２　５６　２４　７６　３６　９６　３２
　１７　１６　３７　３６　５７　３６　７７　６０　９７　９６
　１８　　６　３８　１８　５８　２８　７８　２４　９８　４２
　１９　１８　３９　２４　５９　５８　７９　７８　９９　６０
　２０　　８　４０　１６　６０　１６　８０　３２１００　４０




NO.273 　　　 '99 1/12 　　　Junko 　　　 互いに素（５）

NO.270のオイラー関数表を検証していて、 オイラ−関数の値を求める際には、次の２通りでせめていけばよいということに気づきました。

  1. Ｎ＝ａα　(但し、ａは素数)の時、
    ψ(Ｎ)＝ａα−ａα−１
    (NO.270の定理２)
    特にＮ自身が素数の時は、ψ(Ｎ)＝Ｎ−１
    例えば、ψ(１６)＝ψ(２４)　　　　　　　　
　　　　　　　　＝２４−２３
　　　　　　　　＝１６−８
　　　　　　　　＝８
　　　　ψ(１７)＝１７−１
　　　　　　　　＝１６
  2. それ以外の時は、Ｎ＝ａαｂβｃγ・・・（素因数分解した形）として、 ａα、ｂβ、ｃγ、・・・は互いに素だから、NO.270の定理１より
    ψ(Ｎ)＝ψ(ａα)・ψ(ｂβ)・ψ(ｃγ)・・・
    例えば、ψ(１５)＝ψ(５×３)
　　　　　　　　＝ψ(５)×ψ(３)
　　　　　　　　＝４×２
　　　　　　　　＝８

「ψ（Ｎ）＝６　となる自然数Ｎを求めよ。」を考えてみます。
上記の２つの型別に考えてみます。

  1. ａを素数として、Ｎ＝ａαの時、
    ψ(Ｎ)＝ａα−ａα−１＝ａα−１(ａ−１)＝６
    • ａ−１＝１とすると、ａ＝２。このとき、２α−１＝６よりダメ
    • ａ−１＝２とすると、ａ＝３。このとき、３α−１＝３よりα＝２
      従ってＮ＝３２＝９
    • ａ−１＝３とすると、ａ＝４。このとき、４α−１＝２よりダメ
    • ａ−１＝６とすると、ａ＝７。このとき、７α−１＝１よりα＝１
      従ってＮ＝７１＝７
  2. Ｎ＝ａαｂβｃγ・・・（素因数分解した形）の時、
    ψ(Ｎ)＝ψ(ａα)・ψ(ｂβ)・ψ(ｃγ)・・・＝６
    ψ(ａ)・ψ(ｂ)＝２×３＝６またはψ(ａ)・ψ(ｂ)＝１×６＝６なる組み合わせを探す。
    • ψ(Ｎ)＝３を満たすＮは存在しません。
      ψ(Ｎ)＝ａα−ａα−１＝ａα−１(ａ−１)＝３
      • ａ−１＝１とすると、ａ＝２。
        このとき、２α−１＝３よりダメ
      • ａ−１＝３とすると、ａ＝４。４は素数でないからダメ
    • ψ(Ｎ)＝１を満たすＮを探す。
      ψ(Ｎ)＝ａα−ａα−１＝ａα−１(ａ−１)＝２
      ａ−１＝１とすると、ａ＝２。
      このとき、２α−１＝１よりα＝１
      従ってＮ＝２１＝２
      例外的に、ψ(１)＝１。しかし１では話が進展しない。
      ψ(Ｎ)＝６を満たすのは、前段の話しよりＮ＝７とＮ＝９だから、
      ψ(１４)＝ψ(２)×ψ(７)＝１×６＝６
      ψ(１８)＝ψ(２)×ψ(９)＝１×６＝６

蛇足ながら、ψ(２８)＝ψ(２)×ψ(１４)＝１×６＝６とはなりません。

以上により、ψ（Ｎ）＝６を満たす自然数Ｎは、
Ｎ＝７，９，１４，１８の４つに限る。


さて、オイラ−関数表を見ていて思ったのですが、
「Ｎ≧３に対して、ψ(Ｎ)は必ず偶数となる」ようですね。



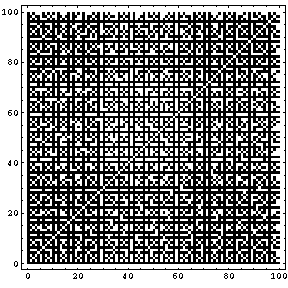
NO.289 　　　 '99 1/18 　　ヴァー 　　　 互いに素（６）

No.260の月の光さんの互いに素の問題を図にしてみました。

横方向のxとして1から100までの自然数を、 縦方向のyとして1から100までの自然数をならべて、 その交点(x,y)について、xとyが互いに素のときには黒、 そうでないときには白という風に色を付けました。

この場合は、黒の割合が6087/10000になりました。(1/20 訂正、白黒逆でした。)



NO.294 　　　 '99 1/19 　　 水の流れ 　　　 互いに素（７）

NO.289で、「ヴァ−」 さんが１００までについて図示してくださいました。
これを、オイラ−関数表で計算すると、確かに
２{ψ(２)＋ψ(３)＋･･･ψ(１００)}＋１＝２×３０４３＋１＝６０８７となっています。
「豊作」さんのレポ−トによれば、
１００００×(６／π２)＝６０７９．２７･･･ですのでまあまあいい感じですね。



NO.301 　　　 '99 1/21 　　ヴァ− 　　　 互いに素（８）

水の流れさんの答え(NO.263)によると
ψ(2)+.....+ψ(100) = 3043なので，

(ψ(2)+.....+ψ(100))/(100(100-1)/2) = 3043*2/100/99 = 3043/4950

となって，私の6087/10000とは違っています．
これは，水の流れさんでは，僕の図(NO.289)でいうと， 左下から右上に向かう対角線より下半分の部分の白黒を 考えていることになっているからです．
つまり，6087=3043*2+1，なんですが， これは3043が下半分の黒の個数なのでそれを2倍して上半分の黒まで考慮し， 最後に(x,y)=(1,1)の部分の黒を付け加えているわけです



NO.302 　　　 '99 1/21 　　Junko 　　　 互いに素（９）

「任意に自然数を２つ選ぶ時、」とありますが、その選び方によって違ってくるわけですね。

同じものを２つ選ぶことを許し、さらにその順序も考慮する(重複順列)と、
全部で１００２＝１００００通りです。
そのうちの６０８７通りですから、６０８７／１００００

１度に２つの自然数をとる(組み合わせ、同じものどうしはありえない)と、
１００Ｃ２＝１００・９９／２＝４９５０
そのうちの３０４３ですから、３０４３／４９５０
戻る