
Weekend Mathematics/コロキウム室/テーマ別
/10.最短シュタイナ−問題
NO.180 10/27 水の流れ 最短シュタイナー問題(1)

NO.183 10/30 Junko 最短シュタイナー問題(2) 三角形、ないし四角形の重心と各頂点を結ぶ線分の和になるのでしょうか?
物理的に考えれば、角頂点において同じ力で引っ張ったときに、
釣り合う点かな? だとしたら、重心ですよね?
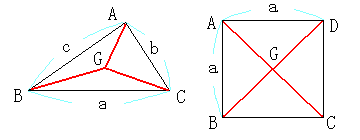

NO.187 11/4 水の流れ 最短シュタイナー問題(3) さて、最短シュタイナー問題は2枚のアクリル板を釘で少し空間を
作って、打ち付けます。洗剤液を水で溶かして、その中に入れて、
持ち上げます。すると、答えがでます。
普通の4角形、正5角形、正6角形までは実験を秋山仁先生は
テレビで放映していました、(5年前)
重心は無関係です。どこの点で結ばれるか?それが分かれば
最短の距離は出ます。その応用が4角形、5角形、6角形と
つながります。

NO.210 11/22 情報処理科2年 最短シュタイナー問題(4) 正方形の頂点A,B,C,Dの位置に4校があり、
この4校を連結するネットワーク
(どの2校もネットワークを通して、行き来できるようにする)
を結ぶ計画があります。
もっとも短い結び方で、何kmが必要でしょうか?
また、その、作図も書いてください。
ただし、1辺の距離をakmとする。
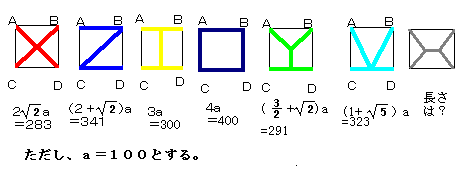
授業の中で出題されたこの問題について、
皆で考えました。
これら設計図の中で、一番短いのは対角線の×印のネットです。
一番右は図だけで、長さは出ていません。
定規で測ってみたら、一番左のものが、対角線の1辺を10cmとして、
だいたい、2√2×10=28.3センチになりました。
次ぎに、一番右はというと、どうも28.3センチより短いみたいです。
でも、途中の交点はどこに取ると良いか?
また、なぜ?と問われると答えられません。

 戻る
戻る