
Weekend Mathematics/コロキウム室/2000.4〜6/NO.95
| NO.815 | 2000.6.1. | Junko | 有限小数と無限小数(2) |
とりあえず1〜15までを表にしてみました。
| N | 1/N | Nの素因数分解 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 0.5 | 2 |
| 3 | 0.33333・・・ | 3 |
| 4 | 0.25 | 22 |
| 5 | 0.2 | 5 |
| 6 | 0.16666・・・ | 2・3 |
| 7 | 0.1425・・・ | 7 |
| 8 | 0.125 | 23 |
| 9 | 0.11111・・・ | 32 |
| 10 | 0.1 | 2・5 |
| 11 | 0.90909・・・ | 11 |
| 12 | 0.08333・・・ | 22・3 |
| 13 | 0.07692・・・ | 13 |
| 14 | 0.07142・・・ | 2・7 |
| 15 | 0.0666・・・ | 3・5 |
1は例外とします。
1/Nが有限小数になっているのは、
Nを素因数分解したときに2と5のみで分解されるものに限るということがわかると思います。
もちろんそれは、10=2・5によるものです。

| NO.816 | 2000.6.1. | Junko | 円錐 (2) |
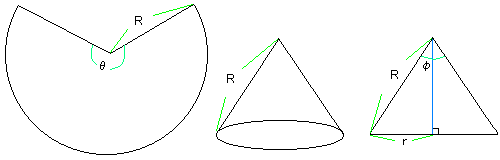
左の図のように扇形の半径をR、内側の角度をθ とします。
弧の長さl=Rθ
できあがった円錐の底面(円)の半径をrとすると円周がl=Rθですから、
2πr=Rθが成り立ちます。
つまり、r=Rθ/2π
一番右の図より、sin(φ/2)=r/R=θ/2π

| NO.817 | 2000.6.2. | 水の流れ | 有限小数と無限小数(3) |
先日、逆数1/Nが有限小数か無限小数かの発見方法を宿題にしました。
一般に、既約分数m/n(m<nの整数)が小数点以下P桁の有限小数
m/n=0.******(P桁)
になったとします。
両辺を10P=100・・・0(P桁)倍することによって、
10P×m/n=******(P桁) は整数になります。
したがって、nは10P×mの約数で、分数が規約ということより、
(m、n)=1 (mとnの最大公約数が1)
つまり n は10Pの約数である。
ところが、10PPの因数分解は2PP・5Pだから、
nは n=2α・5β (ただし、α、β≦Pの整数)
の形をしていなければならない。
また、この過程を逆にたどっていっても n=2α・5βとすると、
m/n は小数点以下P桁の有限小数に展開されます。
以上が、宿題の報告です。

| NO.818 | 2000.6.3. | Junko | 有限小数と無限小数(4) |
NO.812の後半、
Nを自然数とするとき、分数3/Nが、ちょうど小数第3位までの有限小数となるようなNを求めよ、
と言う問題についてです。
小数第3位までですから、
0.001≦3/N
1/1000≦3/N
N/3≦1000
N≦3000
このうち3/Nが有限になるためには、
N=3a・2b・5c(a=0,1、b=0,1,・・・、c=0,1,・・・)という形をしていなければならない。
これらの条件から絞りこんでいくと、以下の14個になると思います。
| N | 3/N | 小数表示 |
|---|---|---|
| 8 | 3/8 | 0.375 |
| 24 | 3/24 | 0.125 |
| 40 | 3/40 | 0.075 |
| 120 | 3/120 | 0.025 |
| 125 | 3/125 | 0.024 |
| 200 | 3/200 | 0.015 |
| 250 | 3/250 | 0.012 |
| 375 | 3/375 | 0.008 |
| 500 | 3/500 | 0.006 |
| 600 | 3/600 | 0.005 |
| 750 | 3/750 | 0.004 |
| 1000 | 3/1000 | 0.003 |
| 1500 | 3/1500 | 0.002 |
| 3000 | 3/3000 | 0.001 |

| NO.819 | 2000.6.6. | 水の流れ | 分銅の問題(1) |
太郎さんは、上皿天秤で目方を計るとき、どんな分銅を何種類か用意し、
一方に計りたい品物、他方に分銅を載せて、両者のバランスを取る。
このとき、分銅の種類はなるべく少なくし、
その組み合わせだけでいろいろとの目方を計るのが好ましい。
分銅の問題というのは、標準の分銅にどんな目方のものを用意すれば、
もっとも能率的かというものです。
一般に、n個の分銅の目方を1g、2g、4g、8g、・・・、2n―1g
に選ぶとすると、分銅の組み合わせを変えば、目方がかならず変わる。
しかも、計れる目方は、0g、1g、2g、3g、・・・、(2n−1) g まで、
1gおきのすべてが可能です。
今、ここには、一方に計りたい品物、他方に分銅を載せる上皿天秤を考えます。
しかも、分銅は1g、3g、9g、27g、81g、243g、729g の7種類でいずれも
1個用意してあります。
このとき、1回だけ使って、計れれる目方は小さい順に、
1g、3g、4g、9g、10g、12g、13g、27g、・・・
となり、1gおきにすべてを計ることができません。ここで、問題です。
問題1:
100gの重さまで、計れる目方は1gから考えて何通りの目方が計れますか。
問題2:
小さい順に1gから目方を計っていく場合、53番目の可能な計り方の目方は何gですか。
また、このときの1個づつの分銅の種類を言ってください。
問題3:
1000gの重さは計ることができますが、1001gの重さを測ることはできません。
これはどうしてでしょうか。数学的に考えてください。
さて、一方に計りたい品物、他方に分銅を載せる上皿天秤でなく、
両方に分銅を載せてもよい上皿天秤を使います。
さらに、n個の分銅の目方を1g、3g、9g、27g、・・・、3n―1g に選ぶとすると、
分銅の組み合わせを変えば、
計れる目方は、0g、1g、2g、3g、・・・、(3n−1)/2 g まで、
1gおきのすべてが可能です。
問題4:
1g、2g、3g、・・・、(3n−1)/2 g まで、
1gおきのすべてが計れることを証明ください。

| NO.820 | 2000.6.7. | 水の流れ | 高度合整数 |
太郎さんは、今、『放浪の天才エルデシュ』という本を読んでいます。
ここの中に、独学で数学を学んだインド人ラマヌジャンの話がありました。
紹介します。
イギルスのケンブリッジ大学での学んだ最初の年、ラマヌジャンは
素数でなく合整数を研究した。合整数とは素数を掛け合わせて「合成した」数のことです。
したがって、6=2×3だから、合整数です。
そして、「高度合整数」という概念を考案しました。
素数にはふたつしか約数がない(1と数自身)が、合整数には約数が少なくとも3つ以上ある。
高度合整数とは、その数未満の合整数より約数の個数が多いものである。
例えば、12は高度合整数である。12は6個の約数を持ち(1,2,3,4,6,12)、
12未満の数には、6個以上を上回る約数をもつものはない。
次ぎに24もそうです。約数が8個あります。
そこで、小さい順に、高度合整数を並べてみます。
2,4,6,12,24,36,・・・、
ラマヌジャンは5万までに25個の高度合整数が含まれており、
6兆7463億2838万8800までの高度合整数を算出してリストを作成した。
ここで、、皆さんにもラマヌジャンと同じように、
この高度合整数を因数分解して、その素因数の指数に着目して、
36の次の高度合整数をみつけてください。
さらに何かの性質みたいなものを発見して下さい。

| NO.821 | 2000.6.13. | Junko | 分銅の問題(2) |
問題1:
0と1の2文字しか使えない3進法だと思えばいいわけです。
10000(三)=81ですから、ここまでで24=16個
10001(三)=82、10010(三)=84・・・ときて、10111(三)=94が最大。
つまり23個
問題2:
5桁以下表記のものが、「00000」をのぞき25−1=31個
従って、6桁表記の最初の数「100000」は32番目
これも含めて、「10□□□□」表記のものが、24=16個
従って、「110000」が48番目
このあたりからは数えてもいいかな?
53番目は、「110101」となります。
分銅は35=243g、34=81g、
32=9g、30=1gの4個で、合計334g
問題3:
3進法表示すると、
1000=1101001(三)だからOK。
しかしながら、
1001=1101002(三)だからだめ。
問題4:
「2=10−1」を利用します。
??と思った人もいるかもしれません。3進法の話です。
きちんとかくと、「2(三)=10(三)−1(三)」ですね。10進法でかくなら「2=3−1」です。
3進法表記した際に、「2」となる桁があったとしたら、それは「10−1」で扱います。
つまり1つ上のおもりをのせると共に、相手方の天秤にもおもりをのせることを意味します。(これが引き算)
そうすれば、最大1+3+・・・3n−1=(3n−1)/2まで、1gきざみで測ることができます。

| NO.822 | 2000.6.17. | Junko | マッチ棒の直角三角形(2) |
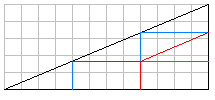
上図のように3辺の長さが5、12、13の直角三角形を考えます。
更に長さ12、5の辺に平行に、1/3のところで分割線(青)を入れます。
元の三角形の面積1/9の三角形3個分づつにわけます。
分け方はいくつかあると思いますが、その1つを(赤)線で示します。
この(赤)線の長さは計算するとちょうど10です。
でもマッチ棒は折るな、といわれるとつらい!

| NO.823 | 2000.6.17. | 月の光 | マッチ棒の直角三角形(3) |
あのようなやり方もあるのかと感心しました。
すみません。書き忘れていましたが「マッチは折ってはいけません」。
火を付けるのも無しです。そのまま使って下さい。
ヒント:それぞれの頂点から他の二つの頂点を結ぶ辺の中点に線を引いて考えて下さい。

| NO.824 | 2000.6.18. | 水の流れ | 整数のわり算 |
nを自然数とするとき、(n+1)から2nまでの連続するn個の整数の積を
1から始まるn個の奇数の積で割った値を求めてください。

 E-mail
E-mail
 戻る
戻る