Weekend Mathematics/コロキウム室/2000.1〜3/NO.91
コロキウム室
| NO.787
| 2000.3.18. | 水の流れ | 無限級数の和(14)
|
皆さん!確率密度関数という用語をご存知ですか。
今日は、この話をします。
確率と密度というのは、それほど似かよったものなのでしょうか。
また、確率が密度だとするならば、平均とか分散というのは、
一体にどんな物理量に対応しているのでしょうか。
位置がxでの密度がp(x)であるような質量1の棒を考えてください。
すると、
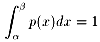
これは(全確率)=1に相当します。
数学の確率分布とは物理では密度分布といいます。
p(x)は数学ではxに対応するy座標、物理では位置xに対応する密度です。
このとき、定積分
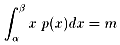
とすると、mは数学では平均、物理では、棒の重心の位置を表しています。
すなわち、数学では平均、物理では重心のことです。
また、
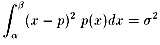
とすると、
σ2は重心を軸に棒を回転したときの「回転質量=慣性モーメント」を表します。
数学では分散、物理では慣性モーメント=2次のモーメントです。
詳しく言うと、軸を中心に回転させると、同じ質量の点でも遠くのものの方が、
「重く」感じられる。
正確には軸からの距離の2乗だけ「重く」なるので、各点ごとのこの「重さ」を寄せ集めたものが、
全体の「慣性モーメント」なのです。
例えば、位置xの密度がp(x)であるコマを考えてください。
分散が小さく、平均からのバラツキが小さいコマは慣性モーメントが小さいので、
フラフラ動きやすく、コマは不安定です。
それに対して、分散が大きく、平均からのバラツキが大きいコマは慣性モーメントが大きいので、
ドッシリト動きにくく、コマは安定しています。
したがって、
NO.776 無限級数の和(12)
の解決に参考になればと思いまして。

| NO.788
| 2000.3.19. | 水の流れ | 数学選手権
|
第48回数学的な応募問題
太郎さんは、新科目「数学基礎」の指導要領の目標を読んでいると、
「数学史的な話題や、数学と人間とのかかわりや、
社会生活において数学が果たしている役割について理解させ、
数学に対する興味・関心を高めるとともに、
数学的な見方や考え方のよさを認識し数学を活用する態度を育てる。」とあります。
したがって、いろいろと数学史の本を読んでいたところ、
ドイツのフリードリッヒ2世が1225年にピザを訪れたとき、
フイボナッチを呼び寄せ、数学御前試合を行っていました。
フイボナッチは出題された次のような問題をたちどころに解いて、
王から賞讃を受けたと言われています。
皆さんのフイボナッチに成り代わって、チャレンジください。
フリードリッヒ2世杯争奪「数学選手権大会」の問題です。
問題1:
x2+5、x2―5がともに平方数となるようにxを求めよ。
問題2:
x+y+z+x2 ,x+y+z+x2+y2 ,
x+y+z+x2+y2+z2がすべて平方数となるように
x,y,zを求めよ。
問題3:
三次方程式 x3+2x2+10x=20 を解け。
(太郎さんの注釈:当時3次方程式の解法は偉大なフイボナッチも発見していませんでしたので、
有理数解がないことを示してください。
また、このときフイボナッチは近似解を見つけています。
皆さんのフイボナッチのように、近似解を見つけてください。
もちろん、今風に、3次方程式の解法で見つけてよいし、ニュートンの近似法でも構いません)
<出典:高校生のための図説数学史:田村三郎・コタニマサオ(現代数学社)>

 E-mail
E-mail
 戻る
戻る
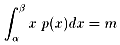
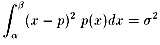

 E-mail
E-mail
 戻る
戻る