
Weekend Mathematics乛僐儘僉僂儉幒乛1999.10乣12乛NO.78
| NO.681 | '99 12/12 | kiyo | 侾俁偺攞悢乮俀乯 |
侾俁偺攞悢偺敾掕朄
X=A亊1000+B 丂1亝A亙99,0亝B亝999 偲偡傞丅
1000==12==-1 (mod 13)
A亊1000==-A (mod 13)
X==B-A (mod 13)

| NO.682 | '99 12/13 | sambaGREEN | 侾俁偺攞悢乮俁乯 |
侾侽侽侾亖俈亊侾侾亊侾俁偱偡偐傜丆
摨條偺庤朄偑丆俈偺攞悢丆侾侾偺攞悢傪尒偮偗傞偺偵巊偊傑偡丅
偨偩偟丆侾侾偺攞悢偺曽偼丆侾偮偍偒偵偲偭偨俀慻偺悢偺崌寁偺嵎偱敾掕
偡傞曽朄偑傛偔抦傜傟偰偄傑偡丅
偙傟偼丆侾侽佭亅侾乮mod 11乯偐傜丆侾侽2k佭侾丆
侾侽(2k+1)佭亅侾偱愢柧偱偒傑偡丅
媡偵丆偙偺敪憐傪巊偆偲丆10002k佭侾丆
1000(2k+1)佭亅侾丂乮偄偢傟傕丂mod丂俈丆侾俁乯丂傛傝丆
壗寘偺悢偱傕丆俁寘偯偮偵嬫愗偭偨悢傪侾偮偍偒偵壛偊偨崌寁偺嵎偱
俈丆侾俁偺攞悢偐偳偆偐敾掕偱偒傑偡丅
椺偊偽丆
| 俙亊1012亄俛亊109亄俠亊106亄俢亊103亄俤 | 佭俙亅俛亄俠亅俢亄俤丂乮mod 7丆13) |
| 佭乮俙亄俠亄俤乯亅乮俛亄俢乯丂乮mod 7,13) |

| NO.683 | '99 12/13 | Junko | 侾俁偺攞悢乮係乯 |
侾俁偱妱傝愗傟傞偐偳偆偐偺敾掕曽朄偼丄
乽壓偐傜俁寘偛偲偵嬫愗傝丄婏悢斣栚偺傕偺偺榓偲丄
嬼悢斣栚偺傕偺偺榓偺嵎偑侾俁偺攞悢側傜妱傟傞丅乿偱偡丅
俈寘偺悢偱偺徹柧
侾俁亊俈俈亖侾侽侽侾傪棙梡偟傑偡丅
倶亖倎亊侾侽俇亄倐亊侾侽俆亄們亊侾侽係亄倓亊侾侽俁亄倕亊侾侽俀亄倖亊侾侽亄倗
丂亖倎亊乮侾侽俁乯俀亄乮倐亊侾侽俀亄們亊侾侽亄倓乯亊侾侽俁亄倕亊侾侽俀亄倖亊侾侽亄倗
丂亖倎亊乮侾侽侽侾亅侾乯俀亄乮倐亊侾侽俀亄們亊侾侽亄倓乯亊乮侾侽侽侾亅侾乯亄倕亊侾侽俀亄倖亊侾侽亄倗
丂亖倎亊乮侾俁亊俈俈亅侾乯俀亄乮倐亊侾侽俀亄們亊侾侽亄倓乯亊乮侾俁亊俈俈亅侾乯亄倕亊侾侽俀亄倖亊侾侽亄倗
丂亖倎亊乮乮侾俁亊俈俈乯俀亅俀亊侾俁亊俈俈亄侾乯亄乮倐亊侾侽俀亄們亊侾侽亄倓乯亊乮侾俁亊俈俈亅侾乯亄倕亊侾侽俀
亄倖亊侾侽亄倗
丂亖侾俁亊乮倎亊侾俁亊俈俈亊俈俈亅俀亊俈俈亄乮倐亊侾侽俀亄們亊侾侽亄倓乯亊俈俈乯亄倎亅乮倐亊侾侽俀亄們亊侾侽亄倓乯
亄倕亊侾侽俀亄倖亊侾侽亄倗
丂佭倎亅乮倐亊侾侽俀亄們亊侾侽亄倓乯亄倕亊侾侽俀亄倖亊侾侽亄倗乮倣倧倓侾俁乯
埲慜偵僇亅僪偺栤戣偱榖戣偵偟傑偟偨丅
侾俁埲奜偺悢傕娷傔偰丄
傑偲傔偲徻偟偄徹柧偑偁傝傑偡丅

| NO.684 | '99 12/14 | 昹揷丂柧枻 | 悢僙儈栤戣 |
悢妛僙儈僫乕侾俀寧崋偺僄儗僈儞僩側夝摎傪傕偲傓栤戣侾偺巹揑夝摎
悢妛僙儈僫乕偺俋俋擭侾俀寧崋偺僄儗僈儞僩側夝摎傪媮傓偺栤戣侾偵偍偄偰丆
巹岲傒偺栤戣傪尒晅偗傑偟偨偺偱丆偄偮傕偺傛偆偵僷僜僐儞偺Visual Basic偱夝偄偰傒傑偟偨丏
杮棃偱偁傟偽丆悢妛僙儈僫乕偵搳峞偡傋偒側偺偱偡偑丆
偙偺傛偆側幾摴側夝摎偑reject偝傟傞偺偼柧傜偐側偺偱丆偙偺僒僀僩偵搳峞偟傑偡丏
怽偟栿桳傝傑偣傫丏偦傟偵掲傔愗傝偺侾俀寧侾侽擔傕夁偓偰偄傑偡丏
栤戣偼埲壓偺捠傝偱偡丏
偡傋偰侾偮偺暯柺偺忋偱峫偊傑偡丏
捈慄倗忋偺揰俹偵挿偝倢偺悅慄俹俼傪棫偰傑偡丏
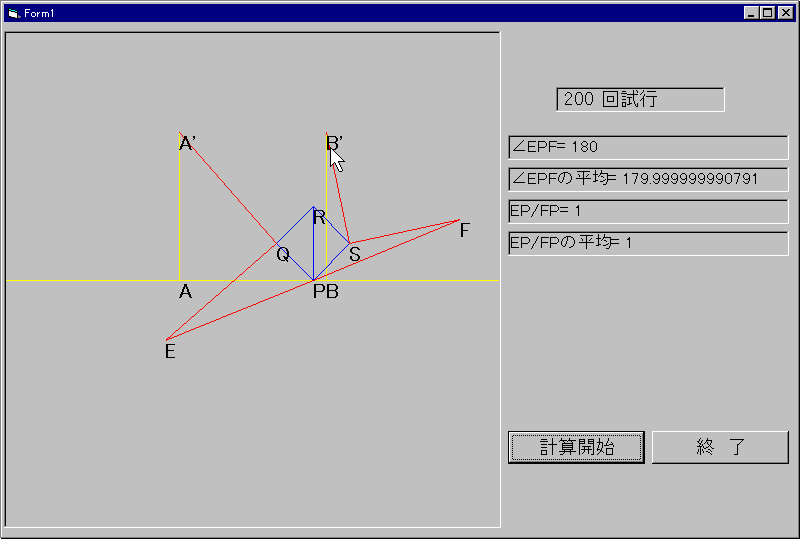
俹俼傪懳妏慄偲偡傞惓曽宍傪恾侾乮徣棯乯偺傛偆偵丆塃傑傢傝偵丆俹俻俼俽偲偟傑偡丏 偮偓偵俹偺嵍塃偵揰俙偲俛傪俙俹亖倢丆俹俛亖倢偲側傞傛偆偵偲傝丆 俙偲俛偐傜丆倗偵娭偟丆揰俼偲摨偠懁偵挿偝俀倢偺悅慄俙俙'偲俛俛'傪棫偰傑偡丏
慄暘俻俙'傪嵍岦偒偵俋侽亱夞揮偟偰俻俤偲偟丆慄暘俽俛'傪塃岦偒偵俋侽亱夞揮偟偰俽俥偲偟傑偡丏 偙偺偲偒丆俤丆俥偼倗忋偵偁偭偰俹偑俤俥偺拞揰偱偁傞偙偲偼柧傜偐偱偡丏
偝偰丆偙傟偐傜偑栤戣偱偡丏
俀偮偺揰俙偲俛偼摦偐偝偢丆俹傪倗忋偺擟堄偺揰偵摦偐偟傑偡乮恾俀乮徣棯乯乯丏 偨偩偟丆俹俼佦倗偲惓曽宍俹俻俼俽偺戝偒偝偼偦偺傑傑偱偡丏 偙偺偲偒丆俤偲俥偼倗偐傜奜傟傑偡偑丆師偺俀偮偺惈幙偼曐偨傟偰偄傑偡丏
偙偺俀偮傪徹柧偟偰偔偩偝偄丏
- 俤丆俹丆俥偼侾捈慄偺忋偵偁傞丏
- 俹偼慄暘俤俥偺拞揰偱偁傞丏
偝傜偵丆俹俼傪倗偵娭偟偰俙俙'傗俛俛'偲斀懳偺岦偒偵偲傞偲偳偺傛偆偵側傞偐峫偊偰偔偩偝偄丏
側偍丆恾俀偱偼俹傪慄暘俙俛忋偵偲傝傑偟偨偑丆 俙俛偺奜偵偲偭偰傕傛偄偟丆俙傑偨偼俛偲堦抳偟偰傕傛偄偙偲傪拲堄偟偰偍偒傑偟傚偆丏
俤丆俹丆俥偑堦捈慄偱偁傞偙偲傪佢俤俹俥亖侾俉侽亱偱帵偟丆
俹偑俤俥偺拞揰偱偁傞偙偲傪俤俹乛俥俹亖侾偱帵偟傑偡丏
俹偺埵抲傪彮偟偢偮曄偊丆偦傟偧傟偺偲偒偺佢俤俹俥丆俤俹乛俥俹傪寁嶼偟丆暯嬒傪媮傔傑偡丏
崌寁俀侽侽夞偺帋峴偱偡偑丆寢榑偑惉傝棫偮偙偲偑暘偐傝傑偡丏
惓曽宍俹俻俼俽偑捈慄倗傛傝壓偺応崌傕傑偭偨偔摨條偵帵偡偙偲偑偱偒傑偡丏
曄悢偺倳倕偺抣傪侾偐傜亅侾偵戙偊傟偽偄偄偩偗偱偡丏
偙偺偲偒丆俤丆俥偺夞揮曽岦偑捈慄倗偺忋偵偁傞応崌偲媡偵側傞偙偲偵拲堄偟傑偡丏
Option Explicit
Sub Form_Load()
Picture1.Scale (-1, 1)-(1, -1)
End Sub
Sub Command1_Click()
'ss9912
Randomize Timer
Dim j, j1, j2, iro0, iro1, iro2, ue As Integer
iro0 = RGB(255, 255, 0): iro1 = RGB(0, 0, 255)
iro2 = RGB(255, 0, 0)
Do
ue = Val(InputBox("惓曽宍PQRS偑捈慄g傛傝忋仺侾丂丂丂捈慄g傛傝壓仺俀丂丂丠", "擖椡"))
Loop Until ue = 1 Or ue = 2
ue = 3 - 2 * ue
Dim shikoukaisuu, kaisuu, machijikan As Long
shikoukaisuu = 200: kaisuu = 0: machijikan = 400000
Dim l, x(9), y(9), d, d_genkai, P_genkai, hen(2) As Double
Dim cos_EPF, kaku_EPF, chuuten, wa1, wa2 As Double
l = 0.3: d_genkai = 0.05: P_genkai = 0.75
Dim ten(9) As String
ten(0) = "A": ten(1) = "B": ten(2) = "A'": ten(3) = "B'"
ten(4) = "P": ten(5) = "Q": ten(6) = "R": ten(7) = "S"
ten(8) = "E": ten(9) = "F"
x(0) = -l: y(0) = 0: x(1) = l: y(1) = 0
x(2) = -l: y(2) = 2 * l: x(3) = l: y(3) = 2 * l
y(4) = 0: y(5) = l * 0.5 * ue: y(6) = l * ue: y(7) = l * 0.5 * ue
Picture2.Cls: Picture3.Cls: Picture4.Cls
Picture5.Cls: Picture6.Cls
For kaisuu = 0 To shikoukaisuu
If kaisuu = 0 Then
x(4) = 0: d = 0: wa1 = 0: wa2 = 0
Else
d = d + (Rnd * 2 - 1) * d_genkai
If Abs(d) > d_genkai Then d = -Sgn(d) * d_genkai
x(4) = x(4) + d
If Abs(x(4)) > P_genkai Then x(4) = Sgn(x(4)) * P_genkai
End If
x(5) = x(4) - l * 0.5: x(6) = x(4): x(7) = x(4) + l * 0.5
For j = 0 To 1
x(j + 8) = ue * (2 * j - 1) * (y(j + 2) - y(2 * j + 5)) + x(2 * j + 5)
y(j + 8) = ue * (1 - 2 * j) * (x(j + 2) - x(2 * j + 5)) + y(2 * j + 5)
Next
For j = 0 To 2
j1 = -4 * (j = 0) - 8 * (j = 1) - 9 * (j = 2)
j2 = -8 * (j = 0) - 9 * (j = 1) - 4 * (j = 2)
hen(j) = (x(j1) - x(j2)) * (x(j1) - x(j2)) + (y(j1) - y(j2)) * (y(j1) - y(j2))
If hen(j) < 0 Then hen(j) = 0 Else hen(j) = Sqr(hen(j))
Next
chuuten = hen(0) / hen(2)
wa2 = wa2 + Sgn(kaisuu) * chuuten
cos_EPF = (hen(2) * hen(2) + hen(0) * hen(0) - hen(1) * hen(1)) * 0.5 / hen(2) / hen(0)
If cos_EPF = 0 Then
kaku_EPF = 90
Else
kaku_EPF = 1 / cos_EPF / cos_EPF - 1
If kaku_EPF < 0 Then kaku_EPF = 0
kaku_EPF = Atn(Sqr(kaku_EPF))
If cos_EPF < 0 Then kaku_EPF = 180 - kaku_EPF
If y(4) > (y(9) - y(8)) / (x(9) - x(8)) * (x(4) - x(8)) + y(8) Then
kaku_EPF = 360 - kaku_EPF
End If
End If
wa1 = wa1 - (kaisuu > 0) * kaku_EPF
Picture1.Cls
Picture1.Line (-1, 0)-(1, 0), iro0
For j = 0 To 1
Picture1.Line (x(j), y(j))-(x(j + 2), y(j + 2)), iro0
Next
Picture1.PSet (x(4), y(4)), iro1
For j = 7 To 4 Step -1
Picture1.Line -(x(j), y(j)), iro1
Next
Picture1.Line -(x(6), y(6)), iro1
For j = 2 To 3
Picture1.Line (x(j), y(j))-(x(j + 3 - (j = 3)), y(j + 3 - (j = 3))), iro2
Picture1.Line -(x(j + 6), y(j + 6)), iro2
Next
For j = 8 To 9
Picture1.Line (x(4), y(4))-(x(j), y(j)), iro2
Next
For j = 0 To 9
Picture1.CurrentX = x(j): Picture1.CurrentY = y(j)
Picture1.Print ten(j)
Next
Picture2.Cls: Picture2.Print kaisuu; "夞帋峴"
Picture3.Cls: Picture3.Print "佢EPF="; kaku_EPF
Picture5.Cls: Picture5.Print "EP/FP="; chuuten
If kaisuu > 0 Then
Picture4.Cls: Picture4.Print "佢EPF偺暯嬒="; wa1 / kaisuu
Picture6.Cls: Picture6.Print "EP/FP偺暯嬒="; wa2 / kaisuu
End If
For j = 0 To machijikan: Next
Next
Beep
End Sub
Private Sub Command2_Click()
End
End Sub

| NO.685 | '99 12/14 | 悈偺棳傟 | 怴暦巻偺愜傝嬋偘乮侾乯 |
偙傟偼丄埶慠僥儗價偱幚嵺偵幚尡傪傗偭偰偄傞偺傪懢榊偝傫偼傒偰偄傑偟偨丅
偝偰丄栤戣偱偡丅岤偝侽丏俀儈儕偺怴暦巻傪侾侽侽夞愜偭偨傜偦偺岤偝偼偳偺偔傜偄偵
側傝傑偡偐丅侾夞愜傞偨傃偵擇攞偺岤偝偵側傝傑偡丅

| NO.686 | '99 12/14 | 悈偺棳傟 | 侾俁偺攞悢乮俆乯 |
NO.682乽sambaGREEN乿偝傫偺拞偵偱偰偔傞侾侽侽侾傪悢妛忋偼乽僔僃僿儔僓乕僥悢乿偲偄偄傑偡丅
傑偨丄乽愮堦栭暔岅乿傊偺楢憐傕偱偒傑偡丅
偙偺暔岅偺偄傢傟偼屻擔偺婡夛偵偟偰丄
侾侽侽侾亖俈亊侾侾亊侾俁偲偄偆楢懕偡傞俁偮偺慺悢偺愊偵側偭偰偄傑偡丅
暯杴側悢偺梡偱偡偑丄側偐側偐嫽枴怺偄悢偱偡丅
巹側偳偼乽俇寘偺惍悢乿乽俇寘偺惍悢乿偲偟偰丄椙偔嫵嵽偵巊偄傑偡丅
侾寘偺値偺悢帤傪巊偭偰丄値亊俁亊俁俈亊侾侽侽侽侾傪寁嶼偟偰偔偩偝偄丅
嬃偒傑偡傛丅
乽僔僃僿儔僓乕僥悢乿偼墹斳偺傛偆偵鉟楉側慺揋側悢側傫偱偡丅
侾亊侾侾亄俀亊俀俀亄俁亊俁俁亄係亊係係亄俆亊俆俆亄俇亊俇俇亖
侾侾亊乮侾俀亄俀俀亄俁俀亄係俀亄俆俀亄俇俀乯偵傕昞傟偰偒傑偡傛丅
懠偵偼丄侾寘偺値偺悢帤傪巊偭偰丄値亊俋亊侾俀俁係俆俇俈俋傕偁傝傑偡丅

| NO.687 | '99 12/15 | 昹揷丂柧枻 | 怴暦巻偺愜傝嬋偘乮俀乯 |
俀100亖(俀10)10亖
侾侽俀係10佮(侾侽3)10亖侾侽30
亪侽.俀噊亊俀100佮侽.俀噊亊侾侽30亖俀亊侾侽23噏
偟偨偑偭偰堦斣嬤偄偺偼俆偺塅拡偺偼偰偱偟傚偆丏
偙偺栤戣偼丆偦偺愄崅俁惗偵暦偐傟丆忋婰偺條偵埫嶼偱寁嶼偟偰丆埿挘偭偨帠偑偁傝傑偡丏
楢拞偼乽壗偐曽朄偑偁傞傫偩両乿偲嫨傫偱偄偨偺偱丆偙偺庬柧偐偟傪偟傑偟偨丏
幚嵺偵偼岤偝侾侽噋偔傜偄傑偱偑尷奅偱偟傚偆丏
偙偺偲偒倶夞愜傝嬋偘偨偲偡傞偲丆
丂丂侽.俀噊亊俀x佮侾侽噋
丂丂亪俀x佮俆侽侽
丂丂亪倶佮俋
丂偮傑傝俋夞偑尷奅偲偄偆帠偱偡丏

| NO.688 | '99 12/16 | 悈偺棳傟 | 僒儞僞偺憽傝暔 |
懢榊偝傫偼丄愭擔僒儞僞偝傫偐傜慺揋側憽傝暔傪捀偒傑偟偨丅
偦偺揱昜偵偼丄侾侽寘偺斣崋偑彂偄偰偁傝傑偡丅
傛偔傒傞偲丄嬼慠偵傕岾塣側悢帤偱偡丅
偦傟偼丄侽偐傜俋傑偱偺悢帤偑侾夞偢偮巊偭偰偁偭偰丄忋偐傜俀寘偺悢偼俀偺攞悢偱丄
俁寘偺悢偼俁偺攞悢偱丄丒丒丒丒丒丒丄値寘偺悢偼値偱乮値亖俀丆俁丆係丆丒丒丒丆侾侽乯
妱傝愗傟偰偄傑偟偨丅
懢榊偝傫偼丄偙偺岾塣側侾侽寘偺悢帤偑懠偵傕偁傞偺偐丄抦傝偨偔側傝傑偟偨丅
亙嶲峫帒椏丗僇亅僪偺栤戣偺
傑偲傔偲徻偟偄徹柧亜

| NO.689 | '99 12/16 | Junko | 怴暦巻偺愜傝嬋偘乮俁乯 |
俀100偲偄偆悢偼堦懱偳偺埵戝偒偄偺偱偟傚偆偐丠
倶亖俀100偲偟偰忢梡懳悢傪偲偭偰傒傑偡丅
偦偆偡傟偽丄寘悢傪抦傞偙偲偑偱偒傞偐傜偱偡丅
| log10倶 | 亖log10俀100 |
| 亖侾侽侽亊log10俀 | |
| 亖侾侽侽亊侽丏俁侽侾侽丒丒丒(忢梡懳悢昞傪尒偰) | |
| 亖俁侽丏侾侽丒丒丒 |
| 侽.俀噊亊俀100 | 亖侽.俀噊亊倎亊侾侽俁侽 |
| 亖俀倎亊侾侽俀俋mm | |
| 亖俀倎亊侾侽俀俇m | |
| 亖俀倎亊侾侽俀俁km |

| NO.690 | '99 12/16 | 悈偺棳傟 | 侾俁偺攞悢乮俇乯 |
乽愮堦栭暔岅乿偺僄僺僜乕僪傪徯夘偟傑偡丅
偙偙偐傜偺暥復偼亙抪偢偐偟偔偰暦偗側偄悢妛俇係偺媈栤丗拠揷婭晇乮阾柧彂朳乯亜偐傜堷梡偟傑偡丅
乽儊僜億僞儈傾偺僒僒儞墹挬乮婭尦俆悽婭偛傠乯偺僔儍僼儕儎乕儖墹偑丄 嵢偵棤愗傜傟偨偙偲偐傜彈惈傪憺傒丄怴偟偄嵢偲堦栭傪夁偛偟偨梻擔嶦偡丄偲偄偆峴堊傪孞傝曉偟偨丅偙偺僄僺僜乕僪偐傜丄悢妛偱偼丄偙偺侾侽侽侾傪僔僃僿儔僓乕僥悢偲屇傫偱偄傑偡丅
偙傟傪抦偭偨戝恇偺柡僔僃僿儔僓乕僥偼丄偙偺偡偝傫偩墹偺怱傪埨傜偐偵偟傛偆偲丄偡偡傫偱墹斳偵側偭偨丅 偦偙偱堦斢拞丄妝偟偄暔岅傪墹偵暦偐偣偨偲偙傠丄墹偼梻擔傕懕偒傪暦偒偨偨偄偨傔丄 墹斳傪嶦偝側偐偭偨丅 偙偆偟偰愮堦栭偑夁偓丄偦偺屻枛塱偔墹偲墹斳偲偼岾暉側恖惗傪憲傞傛偆偵側偭偨丅乿
乽偙偺暔岅偼扤偐偺憂嶌偩傠偆偑丄榖偼峀偔僀儞僪丄儁儖僔儍丄僊儕僔儍丄儐僟儎丄 僄僕僾僩側偳偐傜偺傕偺傪廤傔偨偲偄偆丅 亀傾儔僕儞偺杺朄偺儔儞僾亁亀傾儕僶僶偲巐廫恖偺搻懐亁側偳偑桳柤偱丄栺俁侽侽榖偁傞偦偆偱偡乿

 E-mail
E-mail
 栠傞
栠傞