Weekend Mathematics／コロキウム室／1999.10～12／NO.71

コロキウム室

NO.616

'99 10/1

Junko

試験の採点（２）

問題１

問題１題につき５通りの採点結果が考えられます。(０，５，１０，１５，２０)
全部で５題あるわけですから、５^５＝３１２５

問題２

少なくとも正解が３題で残りは部分点ということですから、正解が３題、４題で場合分けします。
残りの部分点は、５点、１０点、１５点のいずれかであると考えました。
正解３題　_５Ｃ_３×３^２＝９０
正解４題　_５Ｃ_４×３＝１５
９０＋１５＝１０５

問題３

失点が２０点以下で場合分けします。

失点２０点

２０ _５Ｃ_１＝５

１５＋５ _５Ｐ_２＝２０

１０＋１０ _５Ｃ_２＝１０

１０＋５＋５ _５Ｐ_１×_４Ｃ_２＝３０

５＋５＋５＋５ _５Ｃ_４＝５

５＋２０＋１０＋３０＋５＝７０
失点１５点

１５ _５Ｃ_１＝５

１０＋５ _５Ｐ_２＝２０

５＋５＋５ _５Ｃ_３＝１０

５＋２０＋１０＝３５
失点１０点

１０ _５Ｃ_１＝５

５＋５ _５Ｃ_２＝１０

５＋１０＝１５
失点５点

５ _５Ｃ_１＝５
失点０点

０１

７０＋３５＋１５＋５＋１＝１２６

NO.617

'99 10/1

Junko

πの神秘

たまたま本屋さんで「πの神秘」という本を見つけました。
デビッド・バラットナ－著、浅尾敦則訳、ア－ティストハウス　\1600
本のデザインが気に入って買ってきました。円周率πを追求してきた人類の歴史や、πに関するエピソ－ドなどがたくさん書かれています。
そういえば何日か前の朝日新聞にも載っていましたね。

この本と直接関係はないようですが、「π」という映画が上映されているようですね。
本の帯にスト－リ－がかいてありました。
「日常生活に順応できない数学の天才者・マックス。宗教的心理からウォ－ル街の株式事情まで、宇宙の存在をすべて数字で解析できると信じている。「ユークリッド」と名付けた自作コンピューターで、ついに ”神秘の数字”を発見する。その後、彼自身の内部に異常な変化が起こり始める。・・・」
「π」というからには見てみたいのですが、スリラ－っぽいのは苦手なんですよねえ・・・。
残念ながら横浜では上映していませんので、どなたかご覧になった方、感想を聞かせてください。
この映画に関する詳しい情報はこちら。
「π」

NO.618

'99 10/3

水の流れ

三角形の面積（１）

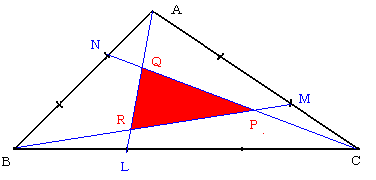
今月の問題を見て、投稿問題です。
三角形ＡＢＣの各辺ＢＣ、ＣＡ、ＡＢを１：２に内分した点をそれぞれＬ、Ｍ、Ｎ　とします。
ＢＭとＣＮ、ＣＮとＡＬ，ＡＬとＢＭの交点をそれぞれＰ、Ｑ、Ｒとします。三角形ＡＢＣの面積は三角形ＰＱＲの面積の何倍でしょうか。
また、一般に、ｍ＜ｎのとき、各辺をｍ：ｎに内分した点をＬ、Ｍ、Ｎとして、同様に、考えてみてください。

NO.619

'99 10/7

Junko

三角形の面積（２）

点Ｒは線分ＢＭ上の点でもあり、線分ＡＬ上の点でもあるので、

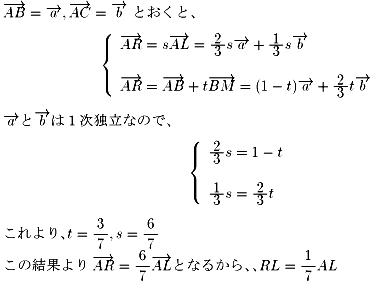
△ＡＢＣの面積をＳとすると、
△ＡＢＬ＝△ＢＣＭ＝△ＣＡＮ＝(1/3)Ｓ
対称性と先ほどの結果から、
△ＢＬＲ＝△ＣＭＰ＝△ＡＮＱ＝(1/3)･(1/7)Ｓ＝(1/21)Ｓ

△ＰＱＲ＝Ｓ－(△ＡＢＬ＋△ＢＣＭ＋△ＣＡＮ)＋(△ＢＬＲ＋△ＣＭＰ＋△ＡＮＱ)
＝Ｓ－(1/3)Ｓ･３＋（1/21)Ｓ･３
＝(1/7)Ｓ

答え　　　　７倍

NO.620

'99 10/8

水の流れ

時計の文字盤（１）

第３０回数学的な応募問題

太郎さんは、先日、時計が止まったので電池の交換に、時計屋に行ってきました。そこには、奇妙にすべての時計が１０時１１分頃で止まっていました。
疑問に思った太郎さんは、店主に、「どうして、この時間にして、飾ってあるのですか？」と聞きました。「お客さんが、末広がりだとおめでたいことが起きると思っていらしゃるからじゃないですか。」と、返事が返ってきました。
太郎さんは、直感的に、長針と短針の角度が１２０度と思ったのと、その２針の間の文字盤の数の和は、全体の和の３分の１になっています。ただし、この時計の文字盤には、１から１２までのすべての数が書かれていますし、秒針はついていません。そこで、問題です。

問題１：

長針と短針が１２０度の角をなし、その２針の間の文字盤の数の和も全体の和の３分の１になっている時刻を求めてください。

問題２：

今度は、長針と短針が１直線に並んでいて、この直線で分けられた２つの部分の文字盤の数の和は、お互いに等しくなっている時刻を求めてください。

太郎さんは、このような不思議な時刻が一日のうちに、何回あるか知っておきたいと思っています。

＜参考文献：「パズル数学入門（田村三郎・藤村幸三郎著）」講談社＞　　　　　　　　

NO.621

'99 10/9

Junko

三角形の面積（３）

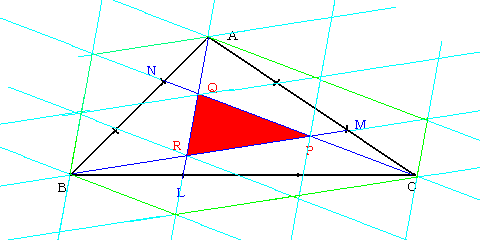
△ＰＱＲの三辺に平行な直線をひいてみました。
黄緑色で囲まれた六角形の部分は、△ＰＱＲの面積のちょうど１３倍になっています。（数えてみてください。）
また別な見方をすれば△ＡＢＣから△ＰＱＲを除いた部分の２倍＋△ＰＱＲとなっています。このことから、７倍と結論づけることができます。

NO.622

'99 10/12

浜田　明巳

三角形の面積（４）

(一部訂正　10/15)

Visual Basicで解答プログラムを作ってみました．
プログラムの内容は以下の通りです．
乱数を使い３点Ａ，Ｂ，Ｃの座標を決定し，点Ｌ，Ｍ，Ｎ，Ｐ，Ｑ，Ｒの座標を求め，ヘロンの公式を使い，△ＡＢＣ，△ＰＱＲの面積を計算し，比△ＡＢＣ／△ＰＱＲを計算する．
この試行を５００回（shikoukaisuu）繰り返し，それぞれの場合の面積比を計算し，面積比の平均を求める．
このプログラムにより，答は７になる事が分かります．
プログラムは２つあり，１つ目は比（r）が１／３の場合で，それぞれの三角形を図示します．
２つ目は比（r）が０と０.５の間の場合で，グラフで描写しています．
またデータをファイルに落とすようになっています
グラフは赤く描かれるのですが，表示後突然黒くなります．
これはｆ(ｒ)＝(１－ｒ＋ｒ²)／(１－２ｒ)²のグラフを上書きする為です．
これにより，答が(１－ｒ＋ｒ²)／(１－２ｒ)²＝(ｎ²＋ｍｎ＋ｍ²)／(ｎ－ｍ)²である事が分かります．

比が１／３の場合

Option Explicit
Const r = 1 / 3
Sub Form_Load()
    Picture1.Scale (-1, -1)-(1, 1)
End Sub
Sub Command1_Click()
    '三角形の問題2
    Randomize Timer
    Dim j1, j2, j3, j4, j, jj, jjj, iro0, iro1, iro2, dame As Integer
    iro0 = RGB(0, 0, 255): iro1 = RGB(255, 255, 0)
    iro2 = RGB(0, 0, 0)
    Dim shikoukaisuu, kaisuu, machijikan As Long
    shikoukaisuu = 500: kaisuu = 0: machijikan = 400000
    Dim x(1, 8), d(1, 2), a(2), b(2), c(2), bumbo, hen(2), s As Double
    Dim menseki(1), wa, hi, d_genkai, hi_genkai As Double
    wa = 0: d_genkai = 0.01: hi_genkai = 10 ^ (-12)
    Dim ten(8) As String
    ten(0) = "A": ten(1) = "B": ten(2) = "C"
    ten(3) = "L": ten(4) = "M": ten(5) = "N"
    ten(6) = "R": ten(7) = "P": ten(8) = "Q"
    Picture3.Cls: Picture4.Cls
    For j1 = 0 To shikoukaisuu
     For j2 = 0 To 2
      For j3 = 0 To 1
       If j1 = 0 Then
        x(j3, j2) = Rnd * 2 - 1: d(j3, j2) = (Rnd * 2 - 1) * d_genkai
       Else
        d(j3, j2) = d(j3, j2) + (Rnd * 2 - 1) * d_genkai
        If Abs(d(j3, j2)) > d_genkai Then
         d(j3, j2) = -Sgn(d(j3, j2)) * d_genkai
        End If
        x(j3, j2) = x(j3, j2) + d(j3, j2)
        If Abs(x(j3, j2)) > 1 Then x(j3, j2) = Sgn(x(j3, j2))
       End If
      Next
     Next
     For j2 = 0 To 2
      j = (j2 + 1) Mod 3: jj = (j + 1) Mod 3: jjj = j2 + 3
      For j3 = 0 To 1
       x(j3, jjj) = (1 - r) * x(j3, j) + r * x(j3, jj)
      Next
      a(j2) = x(1, jjj) - x(1, j2): b(j2) = x(0, j2) - x(0, jjj)
      c(j2) = x(0, j2) * x(1, jjj) - x(0, jjj) * x(1, j2)
     Next
     dame = 0
     For j2 = 0 To 2
      If dame = 0 Then
       j = (j2 + 1) Mod 3: jj = j2 + 6
       bumbo = a(j2) * b(j) - b(j2) * a(j)
       If bumbo = 0 Then
        dame = 1
       Else
        x(0, jj) = (b(j) * c(j2) - b(j2) * c(j)) / bumbo
        x(1, jj) = (a(j2) * c(j) - a(j) * c(j2)) / bumbo
       End If
      End If
     Next
     If dame = 0 Then
      For j2 = 0 To 1: s = 0
       For j3 = 0 To 2
        j = j3 + j2 * 6: jj = ((j3 + 1) Mod 3) + j2 * 6: hen(j3) = 0
        For j4 = 0 To 1
         hen(j3) = hen(j3) + (x(j4, j) - x(j4, jj)) * (x(j4, j) - x(j4, jj))
        Next
        hen(j3) = Sqr(hen(j3)): s = s + hen(j3)
       Next
       s = s * 0.5: menseki(j2) = s
       For j3 = 0 To 2
        menseki(j2) = menseki(j2) * (s - hen(j3))
       Next
      Next
     End If
     Picture1.Cls
     Picture1.PSet (x(0, 0), x(1, 0)), iro0
     For j2 = 2 To 0 Step -1
      Picture1.Line -(x(0, j2), x(1, j2)), iro0
     Next
     For j2 = 0 To 2: j = j2 + 3
      Picture1.Line (x(0, j2), x(1, j2))-(x(0, j), x(1, j)), iro1
     Next
     If dame = 0 Then
      Picture1.PSet (x(0, 6), x(1, 6)), iro2
      For j2 = 8 To 6 Step -1
       Picture1.Line -(x(0, j2), x(1, j2)), iro2
      Next
     End If
     For j2 = 0 To 8 - dame * 3
      Picture1.CurrentX = x(0, j2): Picture1.CurrentY = x(1, j2)
      Picture1.Print ten(j2)
     Next
     Picture2.Cls: Picture2.Print j1; "回試行"
     If menseki(1) >= hi_genkai Then
      For j2 = 0 To 1: menseki(j2) = Sqr(menseki(j2)): Next
      hi = menseki(0) / menseki(1): wa = wa + hi: kaisuu = kaisuu + 1
      Picture3.Cls: Picture3.Print "△ABC/△PQR="; hi
      Picture4.Cls: Picture4.Print "平均                ="; wa / kaisuu
     End If
     For j2 = 0 To machijikan: Next
    Next
    Beep
End Sub
Private Sub Command2_Click()
    End
End Sub

比がｍ／(ｍ＋ｎ)の場合

Option Explicit
Sub Form_Load()
    Picture1.Scale (-1, -40)-(1, 40)
End Sub
Sub Command1_Click()
    '三角形の問題3
    Randomize Timer
    Dim j1, j2, j3, j4, j, jj, jjj, iro0, iro1, iro2, dame As Integer
    iro0 = RGB(0, 0, 0): iro1 = RGB(255, 0, 0): iro2 = RGB(255, 255, 255)
    Dim shikoukaisuu, kaisuu As Long
    shikoukaisuu = 500
    Dim x(1, 8), y, a(2), b(2), c(2), bumbo, hen(2), s As Double
    Dim r, menseki(1), wa, hi, hi_genkai, kizami As Double
    hi_genkai = 10 ^ (-12): kizami = 0.01
    Picture1.Cls: Picture2.Cls: Picture3.Cls
    For j1 = -36 To 36 Step 4
     Picture1.Line (-1, j1)-(1, j1), iro2
    Next
    For j1 = -9 To 9
     Picture1.Line (0.1 * j1, -40)-(0.1 * j1, 40), iro2
    Next
    Picture1.Line (-1, 0)-(1, 0), iro0
    Picture1.Line (0, -40)-(0, 40), iro0
    Picture4.Cls: Picture4.Print "横軸0.1きざみ，縦軸4きざみ"
    Open "sankaku3.dat" For Output As #1
    For r = 0 To 0.5 - kizami Step kizami
     wa = 0: kaisuu = 0
     For j1 = 1 To shikoukaisuu
      For j2 = 0 To 2: For j3 = 0 To 1: x(j3, j2) = Rnd: Next: Next
      For j2 = 0 To 2
       j = (j2 + 1) Mod 3: jj = (j + 1) Mod 3: jjj = j2 + 3
       For j3 = 0 To 1
        x(j3, jjj) = (1 - r) * x(j3, j) + r * x(j3, jj)
       Next
       a(j2) = x(1, jjj) - x(1, j2): b(j2) = x(0, j2) - x(0, jjj)
       c(j2) = x(0, j2) * x(1, jjj) - x(0, jjj) * x(1, j2)
      Next
      dame = 0
      For j2 = 0 To 2
       If dame = 0 Then
        j = (j2 + 1) Mod 3: jj = j2 + 6
        bumbo = a(j2) * b(j) - b(j2) * a(j)
        If bumbo = 0 Then
         dame = 1
        Else
         x(0, jj) = (b(j) * c(j2) - b(j2) * c(j)) / bumbo
         x(1, jj) = (a(j2) * c(j) - a(j) * c(j2)) / bumbo
        End If
       End If
      Next
      If dame = 0 Then
       For j2 = 0 To 1: s = 0
        For j3 = 0 To 2
         j = j3 + j2 * 6: jj = ((j3 + 1) Mod 3) + j2 * 6: hen(j3) = 0
         For j4 = 0 To 1
          hen(j3) = hen(j3) + (x(j4, j) - x(j4, jj)) * (x(j4, j) - x(j4, jj))
         Next
         hen(j3) = Sqr(hen(j3)): s = s + hen(j3)
        Next
        s = s * 0.5: menseki(j2) = s
        For j3 = 0 To 2
         menseki(j2) = menseki(j2) * (s - hen(j3))
        Next
       Next
       If menseki(0) >= hi_genkai And menseki(1) >= hi_genkai Then
        For j2 = 0 To 1: menseki(j2) = Sqr(menseki(j2)): Next
        wa = wa + menseki(0) / menseki(1): kaisuu = kaisuu + 1
       End If
      End If
     Next
     If kaisuu > 0 Then
      y = wa / kaisuu
      Picture2.Cls: Picture2.Print "m/(m+n)(0～.49)="; r
      Picture3.Cls: Picture3.Print "面積比       ="; y
      If r = 0 Then
       Picture1.PSet (0, -y), iro1
      Else
       Picture1.Line -(r, -y), iro1
      End If
      Write #1, r, y
     End If
    Next
    Close #1
    Picture1.Circle (1 / 3, -7), 0.0075, iro1
    Picture2.Cls: Picture2.Print "終了しました．"
    Picture3.Cls: Picture3.Print "f(r)=(1-r+r^2)/(1-2r)^2プロット"
    For r = 0 To 0.5 - kizami Step kizami
     If r = 0 Then
      Picture1.PSet (0, -f(0)), iro0
     Else
      Picture1.Line -(r, -f(r)), iro0
     End If
    Next
    Beep
End Sub
Private Sub Command2_Click()
    End
End Sub
Private Function f(ByVal r As Double) As Double
    f = (1 - r + r * r) / (1 - 2 * r) / (1 - 2 * r)
End Function

データ（m/(m+n)，面積比の順に並んでいます）

0 .999970308041995
.01 1.03091685088192
.02 1.06385487187592
.03 1.09878457255916
.04 1.13607764696844
.05 1.17592162576469
.06 1.21849266823427
.07 1.26406152168348
.08 1.31292805408391
.09 1.36540363718997
.1 1.42189594130447
.11 1.48274870707101
.12 1.54851986034893
.13 1.61960203408582
.14 1.69677976519562
.15 1.78061264811073
.16 1.87188861228095
.17 1.97178347863177
.18 2.0810237524478
.19 2.20338122742966
.2 2.33105591333246
.21 2.47950329959968
.22 2.6415783921597
.23 2.82205700046731
.24 3.02366842506976
.25 3.24842457985923
.26 3.50521575781715
.27 3.79442636580152
.28 4.12387781168895
.29 4.50203963716306
.3 4.93767521461343
.31 5.44392299757662
.32 6.03659244737924
.33 6.73787971424711
.34 7.57442344991707
.35 8.58765709035429
.36 9.8163993417154
.37 11.3445600805142
.38 13.2866250591007
.39 ,15.7459066751137
.4 19.000401013052
.41 23.3980877733627
.42 29.5477885954535
.43 ,38.5153295949182
.44 52.3335906940583
.45 75.2484176839521
.46 117.436295851565
.47 208.583294285575
.48 469.000465047941

NO.623

'99 10/12

Junko

時計の文字盤（２）

ａ時ｂ分（０≦ｂ＜６０）に短針、長針の指す方向を０時の位置から文字通り時計回りに度数法で示すことにします。
短針の位置をｘとすると、ｘ＝３０(ａ＋ｂ／６０)＝３０ａ＋(1/2)ｂ
長針の位置をｙとすると、ｙ＝６ｂ

問題１
（１＋２＋３＋・・・＋１２）／３＝２６
連続する文字盤の数字の合計が２６になっているのは、以下の２通りしかありません。
１１＋１２＋１＋２＝２６
５＋６＋７＋８＝２６

１０時１０～１５分の間に、１１，１２，１，２を囲う形になります。
このとき、ａ＝１０ですから、ｘ＝３００＋(1/2)ｂ、ｙ＝６ｂ
短針と長針の開きが１２０度であることから、
３６０－{３００＋(1/2)ｂ}＋６ｂ＝１２０
これより、ｂ＝１０＋１０／１１＝１０．９０９０・・・
従って、１０時１１分頃となります。
２時５０～５５分の間にも、１１，１２，１，２を囲う形になります。
このとき、ａ＝２ですから、ｘ＝６０＋(1/2)ｂ、ｙ＝６ｂ
短針と長針の開きが１２０度であることから、
３６０－６ｂ＋{６０＋(1/2)ｂ}＋＝１２０
これより、ｂ＝５４＋６／１１＝５４．５４５４・・・
従って、２時５５分頃となります。
４時４０～４５分の間に、５，６，７，８を囲う形になります。
このとき、ａ＝４ですから、ｘ＝１２０＋(1/2)ｂ、ｙ＝６ｂ
短針と長針の開きが１２０度であることから、
６ｂ－{１２０＋(1/2)ｂ}＝１２０
これより、ｂ＝４３＋７／１１＝４３．６３６３・・・
従って、４時４４分頃となります。
８時２０～２５分の間にも、５，６，７，８を囲う形になります。
このとき、ａ＝８ですから、ｘ＝２４０＋(1/2)ｂ、ｙ＝６ｂ
短針と長針の開きが１２０度であることから、
{２４０＋(1/2)ｂ}－６ｂ＝１２０
これより、ｂ＝２１＋９／１１＝２１．８１８１・・・
従って、８時２２分頃となります。

問題２
（１＋２＋３＋・・・＋１２）／２＝３９
連続する６つの文字盤の数字の合計が３９になっているのは、以下の２通りしかありません。
４＋５＋６＋７＋８＋９＝３９
１０＋１１＋１２＋１＋２＋３＝３９

３時４５～５０分の間に、この状態になります。
このとき、ａ＝３ですから、ｘ＝９０＋(1/2)ｂ、ｙ＝６ｂ
短針と長針の開きが１８０度であることから、
６ｂ－{９０＋(1/2)ｂ}＝１８０
これより、ｂ＝４９＋１／１１＝４９．０９０９・・・
従って、３時４９分頃となります。
９時１５～２０分の間にも、この状態になります。
このとき、ａ＝９ですから、ｘ＝２７０＋(1/2)ｂ、ｙ＝６ｂ
短針と長針の開きが１８０度であることから、
{９０＋(1/2)ｂ}－６ｂ＝１８０
これより、ｂ＝１６＋４／１１＝１６．３６３６・・・
従って、９時１６分頃となります。

NO.624

'99 10/12

Junko

三角形の面積（５）

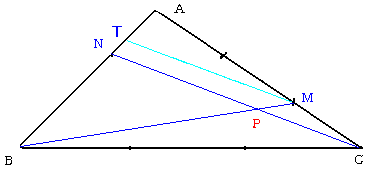
NO.619では、点Ｒの位置ベクトルを求めるのにベクトルの１次独立性を使いました。
「メネラウスの定理」というのがあって、これを使って求めることもできます。
今回は点Ｐでやります。
左図のように、点Ｍを通りＣＮに平行な直線ＭＴをひきます。
ＢＰ：ＰＭ＝ＢＮ：ＮＴ＝ＢＮ：ＮＡ×(ＭＣ／ＡＣ)
ｔ：１－ｔ＝２：１×(1/3)
これより、ｔ＝６／７と求まります。
従って、ＰＭ＝(1/7)ＢＭとなり、以下はNO.619と同様です。

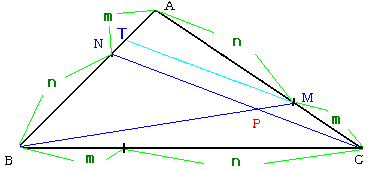
一般に三角形ＡＢＣの各辺ＢＣ、ＣＡ、ＡＢをｍ：ｎに内分した場合を考えます。
先程と同様に、点Ｍを通りＣＮに平行な直線ＭＴをひきます。
ＢＰ：ＰＭ＝ＢＮ：ＮＴ＝ＢＮ：ＮＡ×(ＭＣ／ＡＣ)
ｔ：１－ｔ＝ｎ：ｍ×{ｍ/(ｍ＋ｎ)}
これより、ｔ＝(ｍｎ＋ｎ^２)／(ｍ^２＋ｍｎ＋ｎ^２)と求まります。
従って、ＰＭ＝{ｍ^２／(ｍ^２＋ｍｎ＋ｎ^２)}ＢＭとなります。

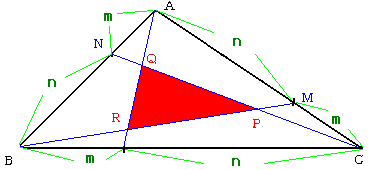
△ＡＢＣの面積をＳとすると、
△ＡＢＬ＝△ＢＣＭ＝△ＣＡＮ＝{ｍ／(ｍ＋ｎ)}Ｓ
対称性と先ほどの結果から、
△ＢＬＲ＝△ＣＭＰ＝△ＡＮＱ＝{ｍ／(ｍ＋ｎ)}･{ｍ^２／(ｍ^２＋ｍｎ＋ｎ^２)}Ｓ
従って

△ＰＱＲ＝Ｓ－(△ＡＢＬ＋△ＢＣＭ＋△ＣＡＮ)＋(△ＢＬＲ＋△ＣＭＰ＋△ＡＮＱ)
＝Ｓ－{ｍ／(ｍ＋ｎ)}Ｓ･３＋{ｍ／(ｍ＋ｎ)}･{ｍ^２／(ｍ^２＋ｍｎ＋ｎ^２)}Ｓ･３
＝{(ｍ－ｎ)^２／(ｍ^２＋ｍｎ＋ｎ^２)}Ｓ

NO.625

'99 10/14

水の流れ

時計の文字盤（３）

第３０回数学的な応募問題の追加問題です。
時計の長針と短針を入れ替えてしまったとき、つまり、長針のほうが短針の動き方をし、短針のほうが長針の動きをするのです。このような時計を見て、文字盤の上では二つの針が正しい時間を指すことのできるのは、半日（１２時間）のうちで何回あるでしょう。この時計は長針と短針が入れ替わっている以外、まったく正確に動いているものとする。　ただし、長針と短針が一致している場合は除いてください。
＜問題の出典：パズル数学入門（田村三朗・藤村幸三朗著）：講談社＞

E-mail

戻る

２０	_５Ｃ_１＝５
１５＋５	_５Ｐ_２＝２０
１０＋１０	_５Ｃ_２＝１０
１０＋５＋５	_５Ｐ_１×_４Ｃ_２＝３０
５＋５＋５＋５	_５Ｃ_４＝５

１５	_５Ｃ_１＝５
１０＋５	_５Ｐ_２＝２０
５＋５＋５	_５Ｃ_３＝１０

△ＰＱＲ	＝Ｓ－(△ＡＢＬ＋△ＢＣＭ＋△ＣＡＮ)＋(△ＢＬＲ＋△ＣＭＰ＋△ＡＮＱ)
	＝Ｓ－(1/3)Ｓ･３＋（1/21)Ｓ･３
	＝(1/7)Ｓ

0	.999970308041995
.01	1.03091685088192
.02	1.06385487187592
.03	1.09878457255916
.04	1.13607764696844
.05	1.17592162576469
.06	1.21849266823427
.07	1.26406152168348
.08	1.31292805408391
.09	1.36540363718997
.1	1.42189594130447
.11	1.48274870707101
.12	1.54851986034893
.13	1.61960203408582
.14	1.69677976519562
.15	1.78061264811073
.16	1.87188861228095
.17	1.97178347863177
.18	2.0810237524478
.19	2.20338122742966
.2	2.33105591333246
.21	2.47950329959968
.22	2.6415783921597
.23	2.82205700046731
.24	3.02366842506976
.25	3.24842457985923
.26	3.50521575781715
.27	3.79442636580152
.28	4.12387781168895
.29	4.50203963716306
.3	4.93767521461343
.31	5.44392299757662
.32	6.03659244737924
.33	6.73787971424711
.34	7.57442344991707
.35	8.58765709035429
.36	9.8163993417154
.37	11.3445600805142
.38	13.2866250591007
.39	,15.7459066751137
.4	19.000401013052
.41	23.3980877733627
.42	29.5477885954535
.43	,38.5153295949182
.44	52.3335906940583
.45	75.2484176839521
.46	117.436295851565
.47	208.583294285575
.48	469.000465047941

△ＰＱＲ	＝Ｓ－(△ＡＢＬ＋△ＢＣＭ＋△ＣＡＮ)＋(△ＢＬＲ＋△ＣＭＰ＋△ＡＮＱ)
	＝Ｓ－{ｍ／(ｍ＋ｎ)}Ｓ･３＋{ｍ／(ｍ＋ｎ)}･{ｍ^２／(ｍ^２＋ｍｎ＋ｎ^２)}Ｓ･３
	＝{(ｍ－ｎ)^２／(ｍ^２＋ｍｎ＋ｎ^２)}Ｓ

１０	_５Ｃ_１＝５
５＋５	_５Ｃ_２＝１０