Weekend Mathematics／コロキウム室／1999.7〜9／NO.69

昨日東京電機大学 で行われた、 「Mathematica 4　その優れたテクノロジー」と題する講演を聞いてきました。

Mathematica 4では、膨大な量の数データを処理する際の効率が高められています。 また、新たなアルゴリズム、言語、インタラクティブ機能などが盛り込まれています。 今回の講演は、この新しい機能のうち、数値計算のスピードと効率のアップ、 何十ものデータの直接のインポートやエキスポート、 グラフィックスやサウンドファイルのフォーマット、 HTMLとTeXの出力能力の向上、データと信号処理に関するサポートの向上、 特定の代数領域での計算サポートなど、特に技術科目を教えることに関連の あるものに焦点を絞って行なわれました。(以上、案内文からの引用)

私が使っている｢mathematica｣の機能はごくごく限られたものですけれど、 そんな私が注目したのは以下の３点です。

• まず、様々なフォ−マット形式の画像(音声も)をインポ−ト、エキスポ−トできると いう点です。
  今までは、｢mathematica｣で描いたグラフなどを、一度bmpに出力した後、 別な変換ソフトを使って、gifなどにかえていました。それがダイレクトにできるわけですから、便利ですし、 画像の質も保てるのではないかと期待できます。
  
• HTMLへの変換が簡単にできることです。(ver3.0でもできますが･･･)
  残念ながら作った数式や画像はgif形式の画像として処理されますが、 コマンド１つで、すべてひっくるめてHTML形式にできるというのは便利だと思います。 例えば、自分の作ったnotebook(ファイルと言ってもいいかな？)を他の人に見てもらいたいと思ったとき。 相手も、｢mathematica｣を使える環境であれば、そのまま送信してみてもらえればいいわけですが、 必ずしもそうとは限りません。 ところが、ブラウザを持っていない人はまずいないでしょうから、HTML形式ならば見てもらうことができます。 もちろん、web上で公開もできます。
  
  更に複雑な数式などを、画像としてではなく、HTMLでかいていくという「MathML」 という規格が開発されているようです。 これにも対応していて、やはりコマンド１つで変換してくれます。 実際にソ−ス表示を見てみると、簡単な数式でもかなり複雑で、手作業でやるのは現実的ではないなという感じです。 ｢mathematica｣を数式をかくときのHTMLエディタ−として使うということができるのではないかと思います。 私も詳しいことはわかりませんが、この「MathML」というものがどの程度一般化しているのか？　 また、ブラウザの方がこれに対応しているのか？　が問題になると思います。
• ｢TeX｣への出力です。(ver3.0でもできますが･･･)
  ｢mathematica｣はとても素晴らしいソフトですが、やはり数式などを表現するという点においては、 ｢TeX｣に勝る物はないと思うのです。 簡単に変換できるのであればありがたいと思います。 (そう思っている人も多いと思います。)
  残念ながら、今回はこの部分の説明　&　デモがありませんでした。 実際に4.0が手に入ったら、やってみましょう・・・！ 近々、発売だそうです。

NO.576 フェルマーの大定理（５）の反例がありました。
山崎愛一さんという方にお願いして、調べてもらいました。

95800⁴+217519⁴+414560⁴=422481⁴

30⁴+120⁴+272⁴+315⁴=353⁴

240⁴+340⁴+430⁴+599⁴=651⁴

27⁵+84⁵+110⁵+133⁵=144⁵

19⁵+43⁵+46⁵+47⁵+67⁵=72⁵

21⁵+23⁵+37⁵+79⁵+84⁵=94⁵

先日、「創立５０周年記念講演会」（神奈川県高等学校教科研究会数学部会主催）があり、 聞く機会がありました。 講師として、東海大学の秋山仁先生でしたが、その中で、 今年度のＩＭＯ（Ｔｈｅ　Ｉｎｔｅｒｎａｔｉｏｎａｌ　Ｍａｔｈｅｍａｔｉｃａｌ　Ｏｌｙｍｐｉａｄ） での日本の結果を話されましたので、過去１０年間まとめて紹介します。
選手は６人で、団体は６人の総得点です。

回	場所	何年	参加国数	日本順位	金メダル	銀メダル	銅メダル
３１	北京	１９９０	５４	２０	０	２	１
３２	ｽｳｴｰﾃﾞﾝ	１９９１	５５	１２	０	３	３
３３	モスクワ	１９９２	５６	８	１	３	１
３４	ｲｽﾀﾝﾌﾞｰﾙ	１９９３	７３	２０	０	２	３
３５	香港	１９９４	６９	１０	１	２	３
３６	カナダ	１９９５	７３	９	１	３	２
３７	インド	１９９６	７５	１１	１	４	０
３８	ｱﾙｾﾞﾝﾁﾝ	１９９７	８２	１２	１	３	１
３９	台湾	１９９８	７６	１４	１	１	３
４０		１９９９	８１	１３	２	４	０

＜参考文献：数学オリンピック’９３〜９８（日本評論社）の付録Ｂから引用＞

A(1)ⁿ+A(2)ⁿ+･･･+A(m)ⁿ=A(m+1)ⁿ (　)は添字
（m、nは自然数、ただし、m=１は除く） （ A(1)A(2)・・・A(m+1)≠０ ）

• m=2 のとき n≧3 で整数解を持たない（大定理）
• m=3 のとき n≧5 で整数解を持たない
• m=4 のとき n≧7 で整数解を持たない
• m=a のとき n≧2a-1 で整数解を持たない
  よって n≧2m-1 のとき整数解を持たない

第２５回数学的な応募問題

太郎さんには、中学校へ通っている子供がいます。 この夏休みの宿題に、次のような円に関する問題が出ていました。

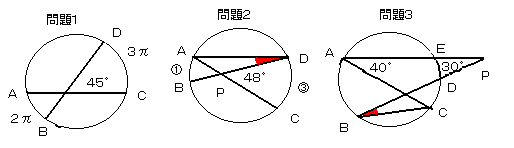
問題１

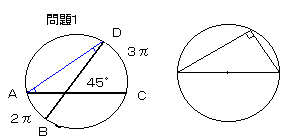
２つの弦ＡＢ，ＣＤが４５゜で交わっている図のような円があります。 弧ＡＢ、弧ＣＤの長さがそれぞれ２π、３πであるとき、 この円の面積を求めよ。

問題２

図のような円があって、∠ＣＰＤ＝４８゜， 弧ＡＢと弧ＣＤの長さの比が１：３のとき、∠ＡＤＢの角度を求めよ。

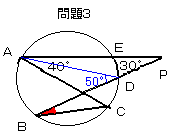
問題３

図のような円があって、∠ＣＡＥ＝４０゜，∠ＡＰＤ＝３０゜で、 弧ＡＢの長さと弧ＣＥの長さの和が半円周の長さであるとき、 ∠ＣＢＤの角度を求めよ。

１．同一の半径を持つ円の弧の長さと、その円周角は比例する (中心角はもちろん比例するし、円周角は中心角の半分ですから)ことから、
∠ＡＤＢ：∠ＤＡＣ＝２：３
また三角形の２つの内角の和は、残る１角の外角に等しいことから、∠ＡＤＢ＋∠ＤＡＣ＝４５ﾟ
これより∠ＡＤＢ＝１８ﾟ、∠ＤＡＣ＝２７ﾟ
弧ＡＢ(２π)に対する円周角が１８ﾟということは、逆に円周角９０ﾟに対する弧の長さが１０πということになり、 これが円周の半分となる。
このことからこの円の半径は１０であることがわかり、従って円の面積は１００π

２．（１）と同様に、∠ＡＤＢ：∠ＤＡＣ＝１：３
また、∠ＡＤＢ＋∠ＤＡＣ＝４８ﾟ
これより∠ＡＤＢ＝１２ﾟ

３．弧ＡＢの長さと弧ＣＥの長さの和が半円周の長さということから、 弧ＡＢに対する円周角と弧ＣＥに対する円周角の和が９０ﾟということになります。
従って、∠ＥＡＣ＋∠ＡＤＢ＝９０ﾟ
∠ＥＡＣ＝４０ﾟより、∠ＡＤＢ＝５０ﾟ
△ＡＤＰに注目すると、∠ＥＡＤ＝２０ﾟ
従って、∠ＤＡＣ＝４０ﾟ−２０ﾟ＝２０ﾟ
同一の弧に対する円周角はもちろん等しいので、 ∠ＤＢＣ＝∠ＤＡＣ＝２０ﾟ

ところで「アルハゼンの定理」というのはどういう定理なのでしょうか？

「アルハゼンの定理」とは一体どんな定理でしょう。
一般に、同一円周上において、円弧の長さとその弦のうえの円周角は当然、比例して、 さらに、中心角にも比例します。ただし、中心角は円周角の２倍です。 さて、これらのことを知っていて、参考図１を見て下さい。

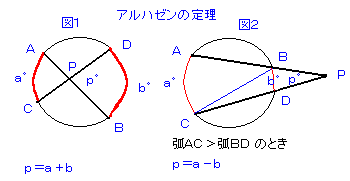
∠ＢＰＤ	＝（弧ＡＣの円周角）＋（弧ＢＤの円周角）
	＝∠ＡＢＣ＋∠ＢＣＤ　　…　（三角形ＢＣＰにおいて、１つの外角は他の２つの内角の和に等しい）

よって、ｐ゜＝ａ゜＋ｂ゜　　＜証明終わり＞

次に、参考図２を見て下さい。

∠ＢＰＤ	＝（弧ＡＣの円周角）−（弧ＢＤの円周角）
	＝∠ＡＢＣ−∠ＢＣＤ…　（三角形ＢＣＰにおいて、１つの外角は他の２つの内角の和に等しい）

よって、ｐ゜＝ａ゜−ｂ゜　　＜証明終わり＞

以上、これが「アルハゼンの定理」です。 このような問題があったら、思い出してください。

第２６回数学的な応募問題

　太郎さんには、中学校へ通っている子供がいます。 この夏休みの宿題に、次のような円に関する問題が出ていました。
前回の「アルハゼンの定理」の応用問題です。

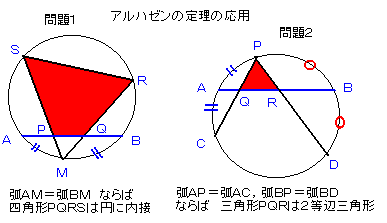
問題１：
参考図１を見てください。 弧ＡＭの長さと弧ＢＭの長さが等しいとき、 赤い四角形ＰＱＲＳは円に内接していることを証明してください。

問題２：
参考図２を見てください。 弧ＡＰの長さと弧ＡＣの長さが等しく、 また、弧ＢＰの長さと弧ＢＤの長さが等しいとき、 赤い三角形ＰＱＲは２等辺三角形であることを証明してください。

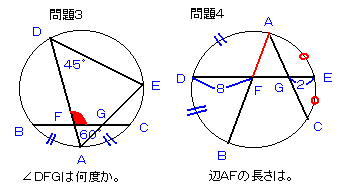
問題３：
参考図３を見てください。 ∠ＤＡＥ＝６０゜，∠ＡＤＥ＝４５゜のとき、 ∠ＤＦＧの角度を求めてください。

問題４：
参考図４を見てください。 辺ＤＦ＝８，辺ＥＧ＝２のとき、 辺ＡＦの長さを求めてください。

問題１：
図のように、ＳＢとＡＲを結びます。
∠ＡＲＭ＝α、∠ＡＲＳ＝βとおく。
∠ＡＲＭ＝∠ＭＳＢ＝α(同じ長さの弧にたつ円周角なので)
∠ＡＲＳ＝∠ＡＢＳ＝β(同じ弧にたつ円周角なので)
従って△ＰＳＢに注目すると、三角形の２つの内角の和は残り１つの外角に等しいことから、 ∠ＡＰＳ＝α＋β、
従って∠ＳＰＢ＝１８０ﾟ−(α＋β)
一方、∠ＳＲＭ＝α＋βなので、∠ＳＲＭ＋∠ＳＰＢ＝１８０ﾟ
向かいあう角の和が１８０ﾟであることから、四角形ＰＱＲＳは円に内接する。

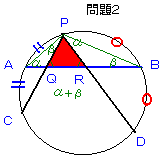
問題２：
図のように、ＡＰとＢＰを結びます。
∠ＢＰＤ＝α、∠ＡＰＣ＝βとおく。
∠ＢＰＤ＝∠ＰＡＢ＝α(同じ長さの弧にたつ円周角なので)
∠ＡＰＣ＝∠ＰＢＡ＝β(同じ長さの弧にたつ円周角なので)
従ってまず△ＰＲＢに注目すると、三角形の２つの内角の和は残り１つの外角に等しいことから、 ∠ＰＲＱ＝α＋β、
同様に△ＰＱＡに注目して∠ＰＱＲ＝α＋β、
従って∠ＰＲＱ＝∠ＰＱＲより△ＰＱＲは２等辺三角形である。

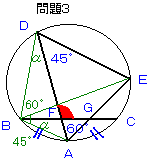
問題３：
図のように、ＡＢ、ＢＥとＢＤを結びます。
∠ＡＢＣ＝αとおくと、
∠ＡＢＣ＝∠ＡＤＢ＝α(同じ長さの弧にたつ円周角なので)
一方、∠ＤＢＥ＝∠ＤＡＥ＝６０ﾟ(同じ弧にたつ円周角なので)
同様に∠ＥＤＡ＝∠ＥＢＡ＝４５ﾟ
従って、∠ＤＢＦ＝６０ﾟ＋４５ﾟ−α
△ＤＢＦに注目すると、∠ＤＢＦ＋∠ＢＤＦ＝(６０ﾟ＋４５ﾟ−α)＋α＝１０５ﾟ
三角形の２つの内角の和は残り１つの外角に等しいことから、 ∠ＤＦＧ＝１０５ﾟ

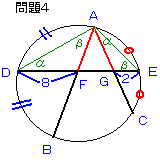
問題４：
問題２と同じ条件ですから、 ∠ＥＡＣ＝α、∠ＤＡＢ＝βとおくと、
∠ＥＡＣ＝∠ＡＤＥ＝α、∠ＤＡＢ＝∠ＡＥＤ＝βとなります。
問題２の結果の通り、△ＡＦＧは２等辺三角形であり、ＡＦ＝ＡＧ＝ｘとします。
図の通り、△ＡＤＦと△ＥＡＧは２角が等しいことより相似となります。
相似比の関係から、８：ｘ＝ｘ：２
これよりｘ＝４

第２７回数学的な応募問題

太郎さんは、以前ＮＨＫの「日本の質問」という番組の中で、 この源氏香の話を聞いていました。
香をたいてその香りを鑑賞する遊びを香道と言います。 香道は平安時代、すなわち１０世紀のころからすでに始まっています。 香道と呼ばれるようになったのは室町時代の１５世紀後半で、 江戸時代に入ると芸道として形が整ってきました。
遊びの中で、二組にわかれて同じ種類のものの優劣を競い合う遊びを物合わせというが、 香合わせは物合わせの一つです。

５種類の香を、それぞれの種類ごとに５包ずつ作る。 すなわち、合計２５袋作る。この２５袋の中から５色を選んで。
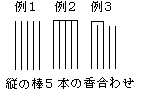
これを順にたく。競技に参加した者は紙に縦の棒５本をたく。 すなわち、例１のように書いておく。
５包の香りを順にかいで（きいて）５種類とも同じなら例２のように横線で引く。
１番目と３番目が同じで、他が違うときは、例の３のようにする。
このように、５種類の香から重複を許して５包の香りを作り、 これをたいて、香りをききわけるとき、一体何通りの違った形を作ることができますか。
これが今回の問題です。できたら、この５本の縦線と横線の違った形を書いてください。
紫式部の「源氏物語」は５４帖あり、この５４帖の一部の題名にこのききわけた香りの記号の名前に あてています。これが源氏香の由来です。

＜補足＞　この源氏香を数学の問題として取り扱ったのは松永良弼（1690頃から1744）である。 松永は関孝和（1640頃〜1708）の孫弟子である。 この源氏香についての解説は、稿本の「断連総術」（1726年）の中に含まれています。

＜出典：数学１００の問題；数学セミナー編集部（日本評論社）＞

E-mail 戻る