
Weekend Mathematics/コロキウム室/1999.1〜3/NO.40
NO.325 '99 2/4 Idaho Potato 漸化式
No.317の水の流れさんの投稿が実話に基づくものかどうか測りかねますが、 似たような話題として、 私が高校時代に実際に経験した話を紹介します。
高校3年の「微分・積分」の試験に、次のような問題が出されました。
次の漸化式で与えられる数列の極限を求めよ。この試験を受けた200人ほどの生徒の大部分は、 数列 { an } の一般項を求めたうえで、 「極限は2である」と解答したのです。 それどころか、その解答に対して「正解」として点数が与えられたのです。
a1 = 1 , an+1 = ( 3an - 4 ) / ( an - 1 )
(この問いかけの意味がわからない方は、 上の漸化式によって a2 を求めてみてください…)

NO.326 '99 2/5 みや 2円の交点を通る直線(6)


NO.327 '99 2/8 浜田 明巳 2円の交点を通る直線(7)
2円の交点を通る直線について
問題の直線は,2円の根軸と呼ばれているものです.
根軸とは,
ただし,一方の円が他方に含まれる場合,根軸は存在しません. この場合も,2円の方程式から直線の方程式が求めることができるので (同心円の場合を除く),これは例外と考えざるをえません.
実際に計算で求めてみます.
一方の円を単位円(x2+y2=1)
他方を(x−a)2+y2=r2(r>0,a>0)
としても,一般性は失われません.
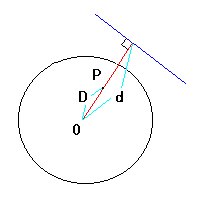
原点をO,A(a,0)とし,共通外接線と2円との接線を
それぞれB,Cとします.
Oから直線ACに垂線ODを下ろします.

これは2円の方程式から,
2次の項を消去してできる直線の方程式に一致します.
ちなみに,3円には,3本の根軸が存在します.
その3本の根軸は1点で交わり,その点を根心といいます.
三角形の5心と同様に,非常に興味深いものです.
以前この根心に関するプログラムを作ったことがあります.
見事に3本の根軸が1点で交わる様はきれいでした.
数学をやっていてよかった,と思う瞬間です.
ただし,このプログラム(N88BASIC)は,ここで発表するには長すぎるので,
またの機会にしたいと思います.

NO.328 '99 2/9 水の流れ ナプキンの問題(1)
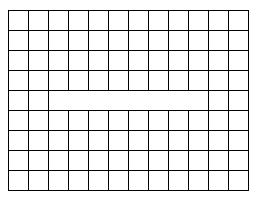
太郎さんのお子さんは、中学校へ12×9の升目模様が
入った給食用ナプキンを持って行きました。
ところが、悪いことに、図のような1×8の升目の位置が汚れて、
切り取るはめになりました。
泣く泣く、帰ってきたお子さんにお父さんは、
心配するなすぐに直してやると言って、
升目にそって2つに切り取り縫い直して、
今度は正方形のナプキンに仕上げました。
太郎さんは、一体どのように、切り取り縫い直したのでしょうか?
お教えてください。

NO.329 '99 2/11 水の流れ 極と極線(1)
太郎さんには、高校に通っているお子さんがいます。
ある日、お子さんに、
「点P(3,2)から、円:x2+y2=16に引いた
2つの接線と円の接点を通る直線の方程式を求めよ。」
という問題を質問されました。
太郎さんは、極と極線の関係を知っていましたから、
答え 3x+2y=16 と言ってにっこりしました。
ところが、お子さんは
「でも、お父さん、この点Pから、円に対して接線を引くことが
できないのだけど、一体どんな直線を求めたことになるの?」
と言われました。
太郎さんに変わって、誰か教えてください。

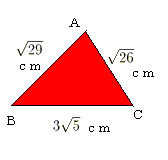
NO.330 '99 2/12 水の流れ 三角形の面積(1)
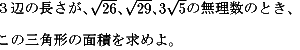

NO.331 '99 2/14 Junko 極と極線(2)

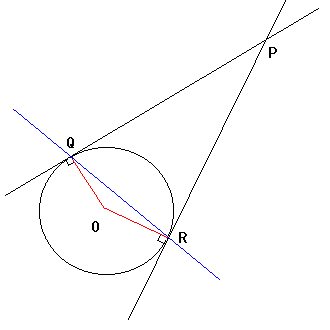

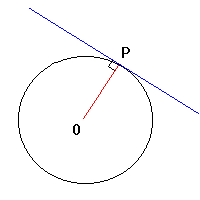
いずれにせよ、直線x1x+y1y=r2
を、点Pを極とする極線というそうです。

NO.332 '99 2/14 Junko 極と極線(3)


NO.333 '99 2/14 Weadore 1999!の桁数(4)
1999!の0の数なのですが、
今年の数学オリンピックの予選にも同じような問題が出ました。
でも、それではその0の数と一桁目から見て0でなくなるときに
最初に出てくる数はいくつか?とのことでした。
ちなみに答は4です。

NO.334 '99 2/14 コウスケ 複素数(1)
複素数で立体は表現する事は可能ですか?
(複素数で空間を表現する事は可能ですか?)
自分としては、第3の方向の成分は作りようがないと思うのですが。

 E-mail
E-mail
 戻る
戻る