Weekend Mathematics/コロキウム室/1998.7〜12/NO.31
コロキウム室
NO.238 '98 12/22 Junko 三角錐と四角錐(2)
合同な正三角形を張り合わせるのですから、
当然その面はなくなるわけで
5+4−2=7かと思いきや・・・。
それではおもしろくないですよね?
でも、側面がつながるようにも思えないので、半信半疑・・・。
模型を作ってみました。
正三角錐の方は、別名正四面体ですから、正三角形を4つつなげます。
正四角錐は正方形のまわりに正三角形を4つ配します。
模型を作ってみてびっくり、まさにぴったり重なるのです。
5+4=5でした。
さて、それでは正三角錐と正四角錐の合同な面を張り合わせた時に、
側面がつながってしまうことの裏付けをしてみます。
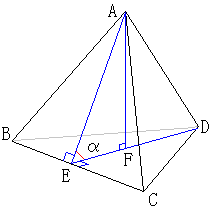 まず正三角錐の隣り合う2つの面がなす角度αを求めてみます。
まず正三角錐の隣り合う2つの面がなす角度αを求めてみます。
左図のように、辺BCの中点をEとすると、
線分AEと、辺BCは直交します。
また頂点Aから面BCDに垂線を下ろし、
その足をFとすると、点Fは三角形BCDの重心です。
線分AEと線分EFのなす角がαというわけです。
(面と面のなす角を調べる時は、両者に垂直な第3の面で切ります。)

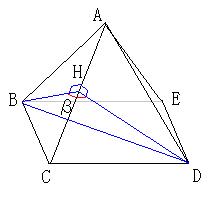 次に正四角錐の隣り合う側面の2つの面がなす角度βを求めてみます。
次に正四角錐の隣り合う側面の2つの面がなす角度βを求めてみます。
辺ACの中点をHとします。
線分BHと線分DHは、辺ACと直交します。
∠BHD=βとなります。

次に、αとβが補角の関係(和が180゚)にあることを示します。
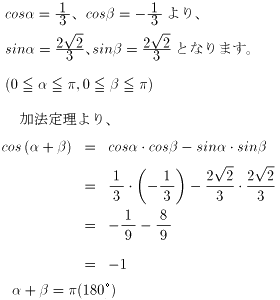
従って、正三角錐と正四角錐の合同な面を張り合わせると、
側面がぴったりつながってしまうのです。

NO.239 '98 12/22 Junko 三角錐と四角錐(3)
正四角錐の両側に正三角錐をぴったりくっつけることができることが
わかりました。
面の数は、4+5+4=5です。
さらにその両側に正三角錐をくっつけたらどうなるのだろうかと、考えました。
やってみると、残念ながら段差ができてしまいます。
そこで、そのことを証明しようと思いました。
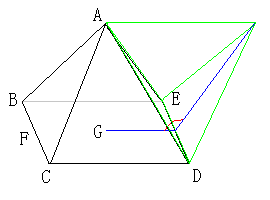
下図のように、正四角錐の底面(正方形の部分)と側面(正三角形の部分)との
なす角γを求めます。
辺BCの中点をFとすると、線分AFとBCは直交します。
また、頂点Aから正方形BCDEに降ろした垂線の足をGとします。
FGとBCも直交します。
従って、∠AFG=γとなります。
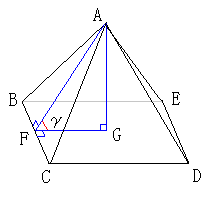

正四角錐と正三角錐を重ねた時に、底面の部分にできる角は、
(α+γ)です。
ですから、次にこの角について調べてみます。
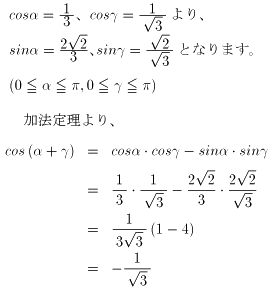
ここまで計算して、はっと気づきました。
正三角錐ではなく、正四角錐ならぴったりだと!!
さっそく正四角錐の模型をもう1つ作り、つけてみると
まさしくぴったりとはまりました。
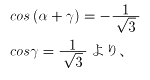
cos(α+γ)の値とcosγの値が異符号であることから、
角(α+γ)と角γは補角の関係にあります。
(証明は、NO.238で同じようなことをしているので省略します。)

つまり、正四角錐と正三角錐を交互に並べていくと、
三角柱の両端を斜めに切ったような立体(面の数は5つ)ができます。
これは、私が作った模型の写真です。
グリ−ンが正四角錐、イエロ−が正三角錐です。

NO.240 '98 12/26 水の流れ 年号と西暦の関係(1)
西暦1999年と平成11年は共に素数です。
過去このように、西暦と年号がともに素数であった年は
キリストが生まれた西暦元年から何回あったでしょう。
また、この次に来るのは平成の年号が変わらないとして、
西暦何年でしょうか。
ちなみに、1999は2から数えて303番目の素数です。

NO.241 '98 12/26 3−6 黄金比(2)
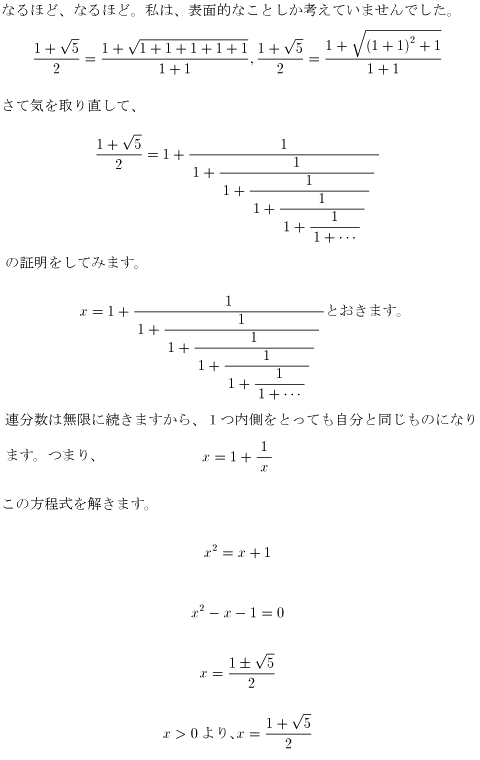
NO.237の1.「1を何回使ってもよいから黄金比を表現しなさい」ですが、
これは、連分数表示かな?とグラス片手に思いました。
Mathematicaで表してみました。
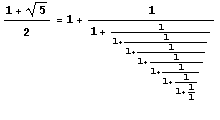
黄金比を連分数表示させて近似したものです。
実際の値は無限に続きます。

NO.242 '98 12/27 Junko 黄金比(3)

NO.243 '98 12/27 みや クリスマスケ−キの問題(3)
問い1
ケーキを碁盤のマスのように9等分します。
これら9個のケーキを次のように分けます。
- Aさん 角2つと真ん中1つ
- Bさん 角1つと辺側2つ
- Cさん 角1つと辺側2つ
問い2
同様に25等分して1人に角の2個を配分し、
後は適当に分けるとうまくいきます。
問い3も36等分して同様な方法で出来ます。
問い4 きっとn人でも大丈夫な気がしますが、
証明は自分には出来ません。
7人までは実験済みです。

NO.244 '98 12/28 Junko クリスマスケ−キの問題(4)
N人で分ける場合についても、同様に方法で分けられることを証明しましょう。
(ただし、ケ−キが細かく分割されるのはちょっとつらい気もしますが・・・。)
ケ−キをN×Nに分割すると、次の3種類のものができます。
- 角・・・側面2つにチョコレ−トあり、全部で4つ
- 横・・・側面1つにチョコレ−トあり、全部で4×(N−2)
- 内・・・側面にチョコレ−トなし、全部で(N−2)2
これらの合計は、
4+4×(N−2)+(N−2)2
={2+(N−2)}2
=N2
これを1人あたりN個、チョコレ−トつきの側面4個になるように分配します。
-
- 1人め・・・角を2個と内を(N−2)個
- 2人め・・・角を1個と横を2個と内を(N−3)個
- 3人め・・・2人めと同様
- 4人め・・・横を4個と内を(N−4)個
- ・・・
- N人め・・・同様
合計を確認すると、
- 角については、2×2=4
- 横については、2×2+4×(N−3)=4×(N−2)
- 内については、(N−2)+2×(N−3)+(N−3)(N−4)=(N−2)2
ですから、OKですね!
-
1人の取り分はなるべくならつながった方がいいと考えると、
最初の1人が角2つというのがひっかかります。
おそらく、問1の「3人」で分けるというところからきているのだと
思いますが・・・。そこで分配に仕方を替えてみます。
- 1人め・・・角を1個と横を2個と内を(N−3)個
- 2人め・・・1人めと同様
- 3人め・・・1人めと同様
- 4人め・・・1人めと同様
- 5人め・・・横を4個と内を(N−4)個
- ・・・
- N人め・・・同様
合計を確認すると、
- 角については、4×1=4
- 横については、4×2+(N−4)×4=4×(N−2)
- 内については、4×(N−3)+(N−4)×(N−4)=(N−2)2
ですから、これでもいいわけですね!
ただし、全員がつながったケ−キを食べるというのは無理のようですね。
-
それなら、これでもいいはず?
- 1人め・・・角を2個と内を(N−2)個
- 2人め・・・1人めと同様
- 3人め・・・横を4個と内を(N−4)個
- ・・・
- N人め・・・同様
合計を確認すると、
- 角については、2×2=4
- 横については、4×(N−2)
- 内については、2×(N−2)+(N−2)(N−4)=(N−2)2

 E-mail
E-mail
 戻る
戻る
 まず正三角錐の隣り合う2つの面がなす角度αを求めてみます。
まず正三角錐の隣り合う2つの面がなす角度αを求めてみます。
 次に正四角錐の隣り合う側面の2つの面がなす角度βを求めてみます。
次に正四角錐の隣り合う側面の2つの面がなす角度βを求めてみます。
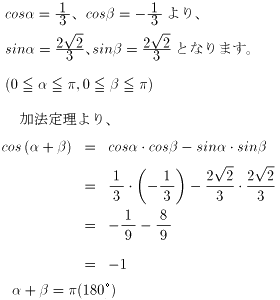




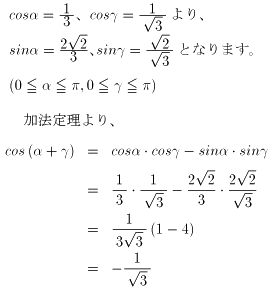
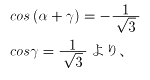

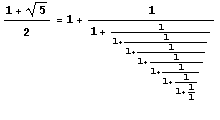

 E-mail
E-mail
 戻る
戻る