
Weekend Mathematics/コロキウム室/1998.7〜12/NO.30
NO.230 12/14 水の流れ 長方形の問題(8) NO.196で、提起した問題です。 最初は順に数えてみましょう。
このM×Nの長方形(M≧Nとする)の中に正方形は
一体いくつありますか?
”How many right angle are
there in a M times N rectanngle?”
以上を、全部足して
注:
1+2+3+・・・+n=n(n+1)/2
12+22+32+・・・+n2=n(n+1)(2n+1)/6
となる公式は知っていますか?
これを利用します。
求める正方形の個数は
N×MN-{1+2+3+・・・+(N-1)}(M+N)+{12+22+32+・・・+(N-1)2}
=N(N+1)(3M-N+1)/6 (答)
また、M=Nのとき、2乗の公式
12+22+32+・・・+n2=
n(n+1)(2n+1)/6
になっています。

NO.231 12/14 Junko 三角錐の体積(4) 今年の夏にNHK教育テレビで、「ワンダ−数学ランド」という番組をやっていました。
講師は秋山仁さんです。その中で、三角錐の体積が話題になっています。
テキストはNHK出版から\900で出ていますが、
三角柱を体積が等しい3つの三角錐に分割するという模型の型紙が
おまけについています。(私はさっそく作ってみました。)
これはかなり説得力があると思います。

NO.232 12/14 水の流れ クリスマスケ−キの問題(1) 24日に、太郎さんは洋菓子店でクリスマスケーキを買って家に帰りました。
箱の中を開けてみると、今日は正方形のチョコレートケーキで、
まわりにもコーティングしてありました。
まわりのチョコレートの量も同じになるように公平に分ける
方法を考えてください。
真上からで良いですから、切り方を教えてください。 問1 太郎さんの家族は3人です。どう分けたら良いでしょうか。
問2 太郎さんの家族は5人です。どう分けたら良いでしょうか。
問3 太郎さんの家族は6人です。どう分けたら良いでしょうか。
問4 太郎さんの家族はn人です。どう分けたら良いでしょうか。
問5 明くる日太郎さんは、何と三角形の同じようなまわりまで
コーティングしてあるケーキを買ってきました。
家族3人で公平に分ける方法を考えてください。

NO.233 12/17 Junko クリスマスケ−キの問題(2)
1辺の長さが2の正方形を座標系の上に置きます。 全体の面積は2×2=4ですから、1人分は(4/3)となります。 次に3本目のナイフですが、これは最初に位置から逆回転して
点(0,-1)超えるかどうかで場合分けをします。 以上の結果をまとめると、どこで切り始めても、
周の長さが(8/3)になるごとにナイフを入れれば、面積も等分されるというわけです。
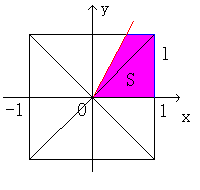
左の図は0゜の位置から切り始めた時の図です。
この時、各頂点の座標は(1,1)、(-1,1)、(-1,-1)、(1,-1)となります。
問題は、面積(これはケ−キの分量にあたります。)が3分割されいる上に
周囲の長さ(これはチョコレ−トでコ−ティングされた側面にあたります。)
も3分割されていればいいわけです。
全体の周の長さは2×4=8ですから、1人分は(8/3)となります。
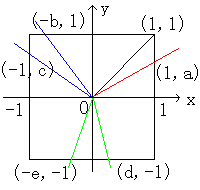 切り始めを、原点(0,0)と点(1,a)を結ぶ線分で切るとします。
(0゜〜45゜で一般化できます。)
切り始めを、原点(0,0)と点(1,a)を結ぶ線分で切るとします。
(0゜〜45゜で一般化できます。)
2本目のナイフは、点(-1,1)超えるかどうかで場合分けをします。
つまりどこで切り始めても、周の長さが(8/3)のところで2本目のナイフを
入れれば、そこまでの面積は必ず(4/3)となるわけです。
2本目のナイフは原点(0,0)と点(-b,1)を結ぶ線分で入れるとします。(b>0)
(1-a)+1+b=(8/3)より、b-a=(2/3)
このとき、面積S=1+(1/2)b-(1/2)a=1+(1/2)(b-a)=1+(1/2)・(2/3)=(4/3)
となり条件に合います。
2本目のナイフは原点(0,0)と点(-1,c)を結ぶ線分で入れるとします。(c>0)
(1-a)+2+(1-c)=(8/3)より、a+c=(4/3)
このとき、面積S=2-(1/2)c-(1/2)a=2-(1/2)(a+b)=2-(1/2)・(4/3)=(4/3)
となり条件に合います。
つまりどこで切り始めても、周の長さが(8/3)のところで3本目のナイフを
入れれば、そこまでの面積は必ず(4/3)となるわけです。
3本目のナイフは原点(0,0)と点(d,-1)を結ぶ線分で入れるとします。(d>0)
2+a-d=(8/3)より、a-d=(2/3)
このとき、面積S=1+(1/2)a-(1/2)d=1+(1/2)(a-d)=1+(1/2)・(2/3)=(4/3)
となり条件に合います。
3本目のナイフは原点(0,0)と点(-e,-1)を結ぶ線分で入れるとします。(e>0)
2+a+e=(8/3)より、a+e=(2/3)
このとき、面積S=1+(1/2)a+(1/2)e=1+(1/2)(a+e)=1+(1/2)・(2/3)=(4/3)
となり条件に合います。
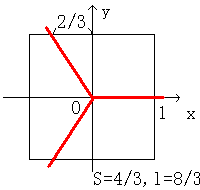
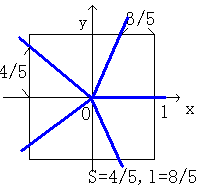
問2.次に、これは3等分に限ったことではないのではないかと思い、
5等分についてもやってみました。
まず5等分ですが、0゜の位置から切り始めて
周の長さが(8/5)になるごとにナイフを入れていくと、
確かに面積が等分されています。
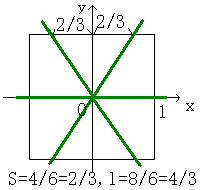
問3.6等分についても同様です。
これを裏付けるためには、周の長さと面積が比例関係にあるということが
証明できればいいわけです。
そこで、0゜の位置(実はどこから切りはじめてもいい)の次に
ナイフを入れるところまでの周の長さl、
面積Sとします。
左の図のように45゜ずつ切り開くと、
いくつかの三角形の和になります。
高さは常に1、底辺の和は周に長さlに一致しますから、
常にl=2Sという関係がなりたつことがわかります。
周の長さと面積は常に比例関係にあるわけですから、任意の場所から切り始めて、
周の長さが(8/n)になるごとにナイフを入れていくと、
面積も等分されるというわけです。
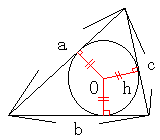
さて次は三角形です。
これも同じように考えられるとしたら、
きっと内心に違いない! と思ったわけです。
3辺の長さをそれぞれa,b,c、周囲の長さをlとすると、
l=a+b+cとなります。
三角形の面積S、内心から各辺までの距離をhとすると、
S=(1/2)ah+(1/2)bh+(1/2)ch=(1/2)・h・(a+b+c)=(1/2)・h・l
となるので、面積Sと周囲の長さlが比例関係にあります。
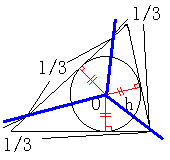
ですから、次のように切ればいいと思います。
必ず内心を通ように切る。
周囲の長さを測り、その1/3になるごとにナイフを入れていく。
これは3等分に限ったことではありませんね。

NO.234 12/19 Idaho Potato リンクバナ−(1) 私からのクリスマスプレゼントとして、
「Weekend Mathematics」のリンクバナーを作りましたので、お送りします。



NO.235 12/19 Junko リンクバナ−(2) 素敵なプレゼントをどうもありがとうございます!!!
このペ−ジにリンクを張ってくださる方が使っていただけるととってもうれしいです。
よろしくお願いします。

NO.236 12/20 水の流れ 三角錐と四角錐(1) 1辺の長さが同じ正三角錘と正四角錐を、
合同な面で合体されたら、何面体の立体ができるでしょうか。
面の数をみてください。
4+5=? の問題です。
さらに、正四角錐を中央にして、左右に2つの正四面体を
合体されると、面の数はどうなるでしょうか?

NO.237 12/21 水の流れ 黄金比(1) 問題 <元旦に 黄金比 を作ろう>

 E-mail
E-mail
 戻る
戻る