NO.1977 不等式の列(5) 2011.9.17. 数学マニア
同じn乗根ならば、累乗の積が大きいほど、不等式は小さい。
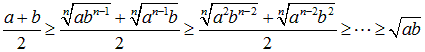
異なるn乗根かつ片方が次数1ならば、累乗が大きいほど、不等式は大きい。
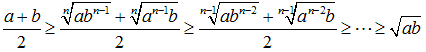
一般に、異なる累乗根のときの比較は、累乗根をそろえると比較可能。
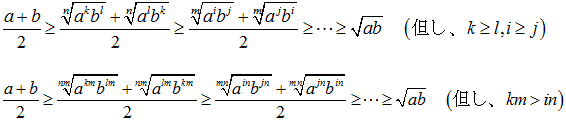
条件付きで
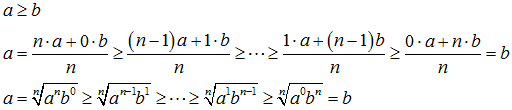
ColloquiumNO.273
|
同じn乗根ならば、累乗の積が大きいほど、不等式は小さい。
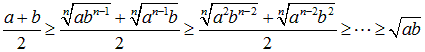
異なるn乗根かつ片方が次数1ならば、累乗が大きいほど、不等式は大きい。
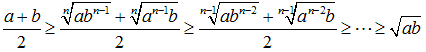
一般に、異なる累乗根のときの比較は、累乗根をそろえると比較可能。
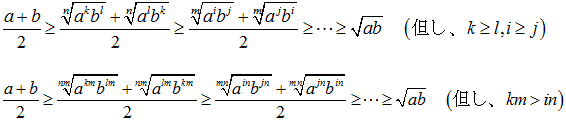
条件付きで
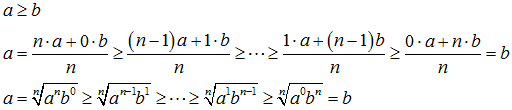
項数が3個以上のときも、同様の不等式の列が存在する。
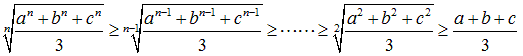
そのため、一般に以下のことが成り立つことを示す。
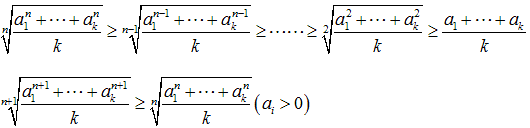
を示す。(項数がk個のとき)…☆
証明

3連勝が一度もないので最初の3試合のなかに必ず負けた試合がある。
また、2連敗も一度もないので、負けた後は必ず勝っている。
よって、なるだけ沢山負けたと考えると、20試合の勝敗は以下の3通りである。
パターン1:XOXOXOXOXOXOXOXOXOXO
→XOの組み合わせが10個
パターン2:OXOXOXOXOXOXOXOXOXOX
→XOの組み合わせが9個
パターン3:OOXOXOXOXOXOXOXOXOXO
→XOの組み合わせが9個
さて、とある組み合わせの後ろからa試合削って、XOの組み合わせの直後にOをa箇所加えたとしよう。
たとえばパターン1で3試合削れば、
XOXOXOXOXOXOXOXOX
XOの組み合わせが8個になるので、下記のaの位置から3個選んでOを加えることになる。
XOaXOaXOaXOaXOaXOaXOaXOaX
よってこの場合の組み合わせは8C3通り。
またパターン1で7試合削れば、
XOXOXOXOXOXOX
XOの組み合わせが6個しかなくなるのでOを7箇所加えることができない。
よって勝敗の組み合わせは以下の462通り。
パターン1
9C1=9、
9C2=36、
8C3=56、
8C4=70、
7C5=21、
7C6=7
パターン2
9C1=9、
8C2=28、
8C3=56、
7C4=35、
7C5=21、
6C6=1
パターン3
8C1=8、
8C2=28、
7C3=35、
7C4=35、
6C5=6、
6C6=1
これに、パターン1、2、3の基本形を加えて、465通り
n x n のマス目に題意に合うように○を入れてあるとする。
同じ行・列にある○を順に結んでいくと、一順して元に戻ります。
一順ですべての行・列の○を結べる場合の数を g (n) とします。
(例) 5 x 5 の○を順次結んだ場合。
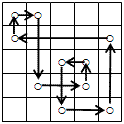
場合の数は、以下の式で表せます。
g (n) = (n・(n-1)・(n-1)・(n-2)・(n-2)・・・2・2・1・1)/2
n が、2, 3 の場合は、1順で全てを結ぶ場合しかないので、
f (2) = g (2) = 1
f (3) = g (3) = 6
4 x 4 の場合は、全部を通って元に戻る場合 g (4) と、
2行2列分を通って元に戻るルートが2つある場合がある。後者の場合の数は、
4C2・4C2・g (2) ・g (2) /2
である。
(選んだ2行2列と残った2行2列が、入れ替わった場合は、重複して数えているので、2で割る必要がある。)
従って、
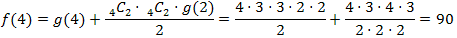
5 x 5 の場合は、全部を通って元に戻る場合g (5) と、
2行2列分を通って元に戻るルートと3行3列分を通って元に戻るルートがある場合がある。
後者の場合の数は、
5C2・5C2・g (2) ・g (3)
従って、
6 x 6 の場合は、
(1)全部を通って元に戻る場合
g (6) = (6・5・5・4・4・3・3・2・2)/2 = 43200
(2)2行2列分を通って元に戻るルートと4行4列分を通って元に戻るルートがある場合
6C2・6C2・g (2) ・g (4) =(6・5・6・5・72)/(2・2) = 16200
(3)3行3列分を通って元に戻るルートが2つある場合 (重複を考慮し、2で割る)
6C3・6C3・g (3) ・g (3) /2=(6・5・4・6・5・4・6・6)/(3!・3!・2) = 7200
(4)2行2列分を通って元に戻るルートが3つある場合 (重複を考慮し、3!で割る)
6C2・6C2・g (2) ・4C2・4C2・g (2) ・g (2)/3!=(6・5・6・5・4・3・4・3)/(2・2・2・2・3!)=1350
以上を加えることにより、f (6) = 67950
一部修正 9/5 22:30
自然数には素数と合成数がある。ただ、1は素数でも合成数でもない。単位数という。
ここで、合成数であり、自然数が2、3、5のいずれでも割り切れないとき、準素数と呼ぶことにする。
準素数を小さい順に3つ挙げると、49、77、91です。2011以下の素数は305個ある。
2011以下の準素数はいくつあるか。
注:この記事に関する投稿の掲載は、2011年9月26日以降とします。
【1】
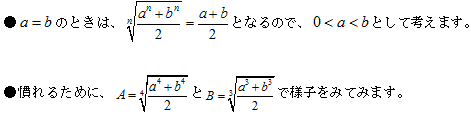
それぞれ3×4=12乗して下線部の差をとります。
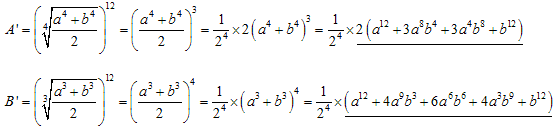
途中、相加平均と相乗平均の関係を使います。
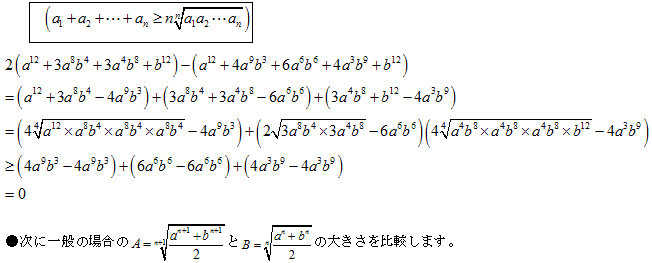
次のようにそれぞれ 乗して下線部の差をとります。
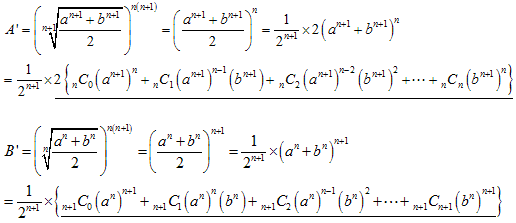
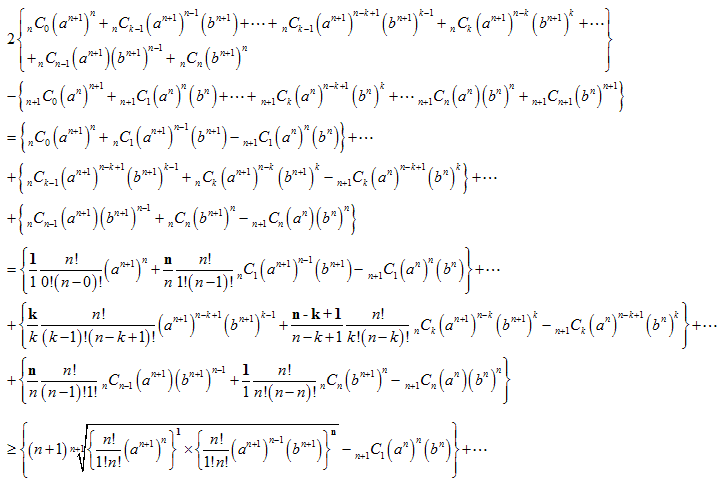
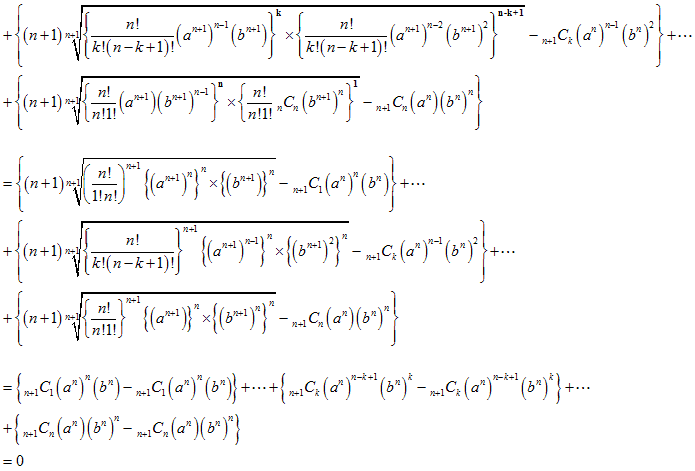
【2】
●練習
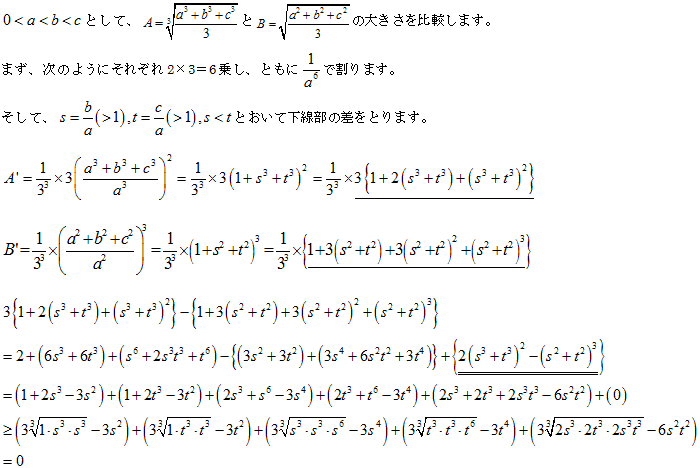
(2重下線部は【1】から正です)
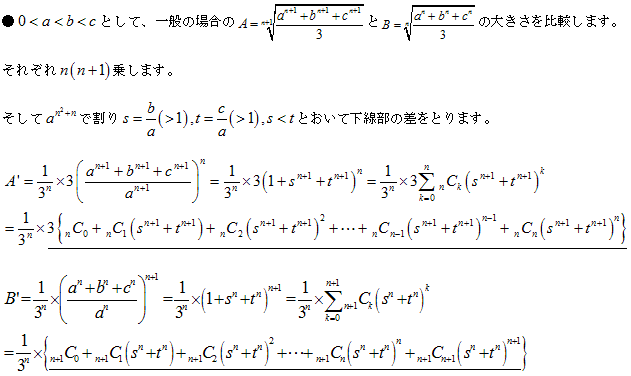
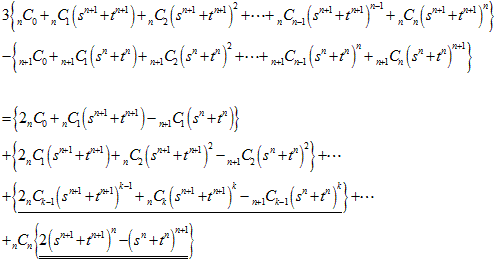
(2重下線部は【1】から正です)
この形にしてそれぞれの中括弧{ }のところが正であることを調べます。
k番目の中括弧{ }の1重下線のところは、
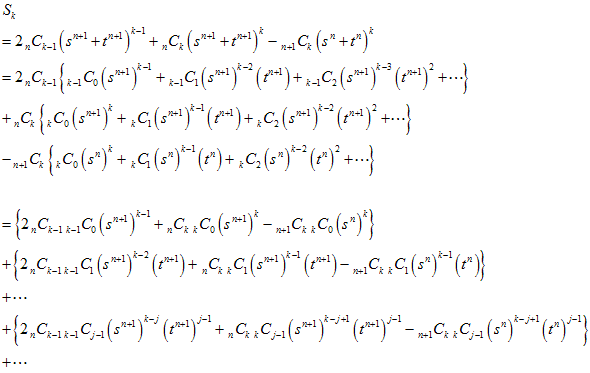
まず、
最初の中括弧{ }の部分は、
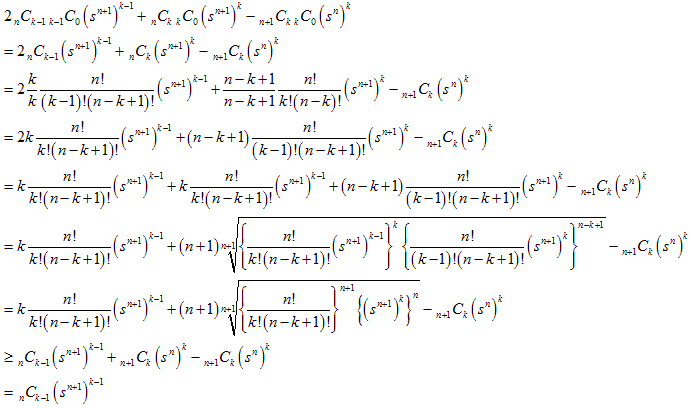
となり係数の1つ分が余ります。
そこで、次々1つ分を次の中括弧{ }に移していき、
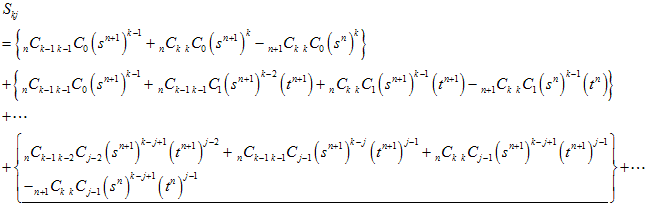
として考えます。
この形にしてそれぞれの中括弧{ }のところが正であることを調べます。
ここで、j番目の中括弧{ }の1重下線のところを計算します。
わずらわしいので、係数、底、指数を次のように表すことにします。
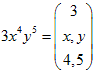
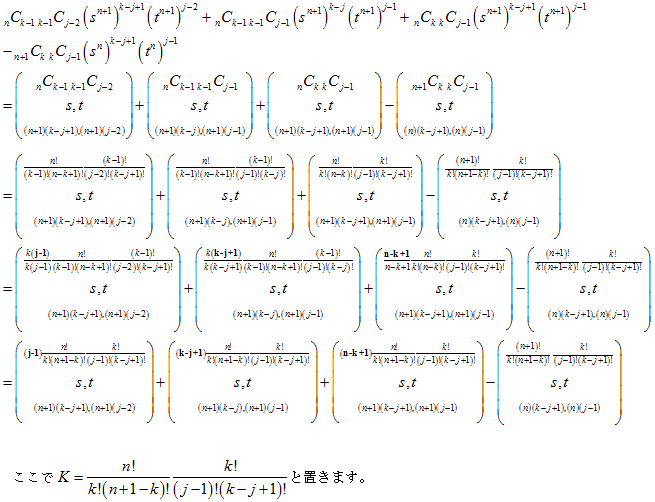
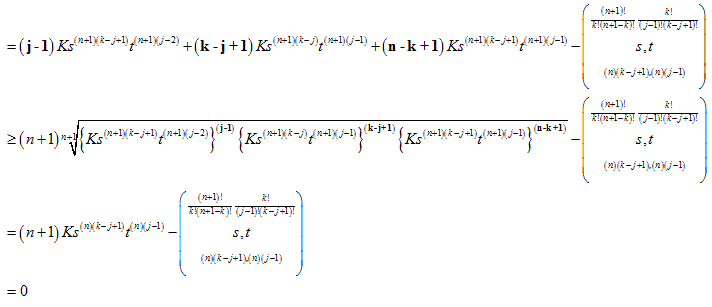
以上から3つになっても成立が確認できました。
●試合結果を次のように表すことにします。
勝ちは、連勝数で、負けには連敗がないので、ハイフン「-」で表します。
{×○○×○×}は、{-2-1-}とします。
●勝ちが多い順に考えていきます。
・15勝以上はありません。
・14勝6敗は、次の場合以外ありません。
(1) {2-2-2-2-2-2-2}の1通り
・13勝7敗は、次の場合です。
(1) {2-2-2-2-2-2-1-}は、1の位置を考えて、7通り
(2) {-2-2-2-2-2-2-1}も、1の位置を考えて、7通り
(3) {2-2-2-2-2-1-1-1}は、同じものを含む順列を考えて、8!/5!3! = 56通りなので、計70通り
・12勝8敗は、次の場合です。
(1) {-2-2-2-2-2-1-1-}は、同じものを含む順列を考えて、 7!/5!2! = 21通り
(2) {2-2-2-2-1-1-1-1-}は、同じものを含む順列を考えて、 8!/4!4! = 70通り
(3) {-2-2-2-2-1-1-1-1}は、同じものを含む順列を考えて、 8!/4!4! = 70通り
(4) {2-2-2-1-1-1-1-1-1}は、同じものを含む順列を考えて、9!/3!6! = 84通りなので、計245通り
・11勝9敗は、次の場合です。
(1) {-2-2-2-1-1-1-1-1-}は、同じものを含む順列を考えて、 8!/3!5! = 56通り
(2) {2-2-1-1-1-1-1-1-1-}は、同じものを含む順列を考えて、9!/2!7! = 36通り
(3) {-2-2-1-1-1-1-1-1-1}は、同じものを含む順列を考えて、9!/2!7! = 36通り
(4) {2-1-1-1-1-1-1-1-1-1}は、1の位置を考えて、10通りなので、計138通り
・10勝10敗は、次の場合です。
(1) {-2-1-1-1-1-1-1-1-1-}は、1の位置を考えて、9通り
(2) {1-1-1-1-1-1-1-1-1-1-}の1通り
(3) {-1-1-1-1-1-1-1-1-1-1}の1通りなので、計11通り
・9勝以下はありません。
●以上465通りです。
n x n のマス目に、◯をいれる。
縦、横それぞれ、いずれから見ても◯が2個に見える入れ方は何通り?
わたしのアプローチ...
2*2...f(2)=1
3*3 のとき...◯のない場所で考えると...3!...f(3)=6
f(4)=(4*3/2)*(3+3*2*2)=90
f(5)=(5*4/2)*(4*f(3)+4*3*3*f(2)+4*3*3*2*2)=2040
f(5)までは、これでよさそうなことは...数列大辞典で確認できた...?
f(6) の出し方が分かりません...^^;...
 ●準備
●準備
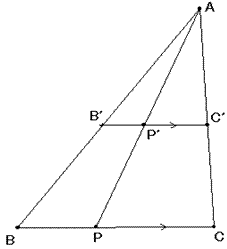
△ABCにおいて、BC//B’C’とします。
・右上の図で頂点Aから辺BCに直線を引きます。
すると、△AB’P’∽△ABPなので、AP’:P’P=B’P’:BPです。
同様に、△AC’P’∽△ACPなので、AP’:P’P=C’P’:CPです。
よって、B’P’:BP=C’P’:CPです。(B’P’・CP=C’P’・BP)
表現を変えると、B’P’:P’C’=BP:PCとなります。
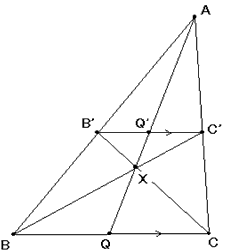 ・右中の図でBC’とCB’の交点をXとします。
・右中の図でBC’とCB’の交点をXとします。
さらに、AからXを通り底辺BCに直線を引きます。
すると、△XC’Q’∽△XBQなので、XQ’:XQ=C’Q’:BQです。
同様に、△XB’Q’∽△XCQなので、XQ’:XQ=B’Q’:CQです。
よって、C’Q’:BQ=B’Q’:CQです。(C’Q’・CQ=B’Q’・BQ)
表現を変えると、B’Q’:Q’C’=CQ:QBとなります。
また、上の内容から、右中の図について、B’Q’:Q’C’=BQ:QCです。
下線の式を比較して、右中の図について、BQ=CQです。
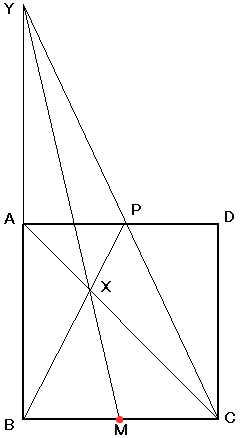 ●解答
●解答
・正方形の辺ABを延長し、延長上に適当にYをとります。
・YCとADの交点をPとします。
・BPとACの交点をXとします。
・YからXを通りBCに線を引きます。
・すると、MがBCの中点です。
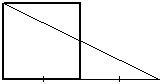
●おまけ
定規と鉛筆が使えるのですから、1辺の長さを定規に記し、
底辺を1辺の長さだけ延長し、一番遠い頂点と結べば、
辺の中点が簡単にとれます。(普通は、こうすると思います)
○NO.1962の解答をみたあとで作りました。
この素晴らしい解答は、25の剰余を使っていますが、25進数を考えてもいいかなと思いました。
同じ内容になりますが。
●25進法で数を表すことを考えます。
0から24を表す数字を次のように決めます。(IとOは紛らわしので使いません)
{ 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F,G,H,J,K,L,M,N,P,Q }
例えば、24はQ、25は10、50は20、55は25となります。
(下線が25進法で表した数です)
●n日目に読む本の冊数をf(n)で表します。
1日目からn日目まで読んだ合計の本の冊数をg(n)とします。
つまり、g(n)=f(1)+f(2)+・・・+f(n)です。
ここで、25進法で表したg(n)の下1桁に注目します。
便宜的に、g(0)=0とします。
g(n)は、g(0)からg(31)まで、32個あります。
数字は25種類あるので、最低でも32-25=7個は、下1桁が同じです。
下1桁が同じで差g(n)-g(m)が50(20)になるのは次の6通りです。
①55-5(25-5), ②54-4(24-4), ③53-3(23-3),
④52-2(22-2), ⑤51-1(21-1), ⑥50-0(20-0)
問題の内容から、これら6通りのそれぞれは2個以上あることはありません。
これら以外は、差をとると、25(10)になります。
だから、最低でも1組は差が25(10)になるところがあります。
g(n)-g(m)=25(10)とすれば、f(m+1)からf(n)までの連続した
n-m-1個の合計が25(10)となります。
