ColloquiumNO.272
|
37年前に聞いた問題を提出します。
正方形の一辺の中点を作図により求めなさい。
作図の条件は、定規（目盛りのないもの）1枚と、鉛筆だけです。
（抽象的に表現すると、線分を延長することと直線又は線分の交点を通る直線のみで作図）
レベルとしては小学校高学年ですが、やわらかい発想が必要かなと思います。
今年のプロ野球は勝敗に異変があるようです。主な要因は低反発力にしたボールや
東日本大震災により節電のため延長戦は3時間30分を超えた場合は新しいイニングに入らないなどがあります。
そこで、ある球団が1ヶ月２０試合を行ったところ、次のことが分かりました。ただし、引き分けはありません。
１．３連勝が一度もない。
２．２連敗も一度もない。
このような現象のとき、20試合の勝敗の起こりうるすべての場合は何通りあるか考えてください。
ちなみに最初の３試合は（○、○、×）（○、×、○）（×、○、○）（×、○、×）の４通りです。
○は勝ち、×は負けの記号としてある。
注：この記事に関する投稿の掲載は、2011年９月５日以降とします。
１．
ｘ+√（ｘ2-1）＝ｔ・・・(1) は変形すると
ｘ＝（ｔ+1/ｔ）/2・・・・(2)
になります。よって
ｄｘ＝（1-1/ｔ2）/2 ｄｔ
ここでｔを積分すると
∫（ｘ+√（ｘ2-1））ｄｘ＝∫（ｔ-1/ｔ）/2 ｄｔ・・・(3)
一方で√（ｘ2-1）＝χと置き（(1)ｔ＝ｘ+χ）、∫χｄｘ＝Ｉと置き(3)左辺を書き換えると
(3)左辺＝ｘ2/2 +Ｉ
I＝(3) - ｘ2/2・・・・(4)
ここで(3)の右辺ｔについての積分を求め(1)を代入すると
(3)＝（ｔ2/2 - logｔ）/2+C＝（ｘ2+ｘχ- 1/2 - log（ｘ+χ））/2+C
χを戻し、定数項を成分乗数Cに含めると、(4)から
I=（ｘ√（ｘ2-1）-log（ｘ+√（ｘ2-1）））/2
２．
この問題は三角形OPｐと（1）の1からｐまでの定積分（正のみ）との差に帰結される
ので次のように示される。
ΔOPｐ＝Ａ１＝ｐ（√（ｐ2-1））/2
１．の1からｐまでの定積分I
Ａ２＝（ｐ√（ｐ2-1）-log（ｐ+√（ｐ2-1）））/2
Ｓ＝Ａ＝Ａ１−Ａ２＝log（ｐ+√（ｐ2-1））/2
３．
Ｓ＝θ/2＝log（ｐ+√（ｐ2-1））/2
これを変形して
√（ｐ2-1）＝ｅθ-ｐ
両辺二乗してｐについて解くと
ｐ＝（ｅθ+ｅ-θ）/2
２．からｑ＝√（ｐ2-1）なので左式を代入整理すると
ｑ＝（ｅθ-ｅ-θ）/2
４．
３．よりｘ＝（ｅθ+ｅ-θ）/2とおくと
√（ｘ2-1）＝（ｅθ-ｅ-θ）/2
ｄｘ＝（ｅθ-ｅ-θ）/2 ｄθ
これらから
Ｉ＝∫（（ｅθ-ｅ-θ）/2）2 ｄθ
展開整理して積分すると
Ｉ＝（ｘ√（ｘ2-1）-log（ｘ+√（ｘ2-1）））/2+Ｃ
となり １．と同じ結果が得られます
５．
ｕ＝2ｘ+1とおくと
ｄｘ＝1/2 ｄｕ
∫√（ｘ（ｘ+1））ｄｘ＝1/4∫（√（ｕ2-1））ｄｕ
となるので、４．の結果を利用し
（ｕ√（ｕ2-1）-log（ｕ+√（ｕ2-1）））/8+Ｃ
が得られ、ｕ＝2ｘ+1を代入すると
∫√（ｘ（ｘ+1））ｄｘ＝（（2ｘ+1）2√（ｘ（ｘ+1））-log（（2ｘ+1）+2√（ｘ（ｘ+1）））/8+Ｃ
ｎ日目までに f(n) 冊読んだことにすると、f(0)＝0，f(31)＝55 です。
f(b)−f(a)＝25 になれば、(a＋1)日目〜b日目に 25冊読んだことになります。
f(n) を 25 で割った余りを g(n) とすれば、
g(0)〜g(31) の32個の値は、0〜24 の25種類です。
従って、g(a)＝g(b)，a＜b を満たす(a，b)は少なくとも７組あります。
この７組については、f(b)−f(a)＝25 または f(b)−f(a)＝50 ですが、
f(b)−f(a)＝50 を満たすのは、全部考えても、
(f(a)，f(b))＝(0，50)，(1，51)，(2，52)，(3，53)，(4，54)，(5，55) の６組だけですので、
f(b)−f(a)＝25 を満たすのは１組はあるはすです。
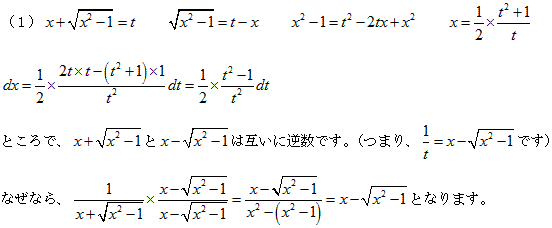
以上を踏まえて、
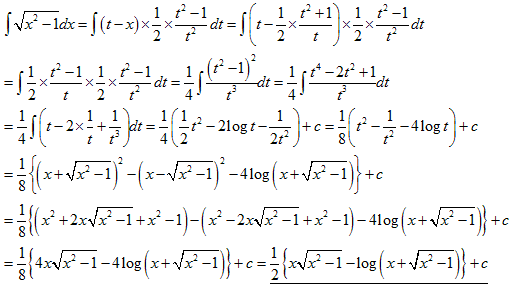
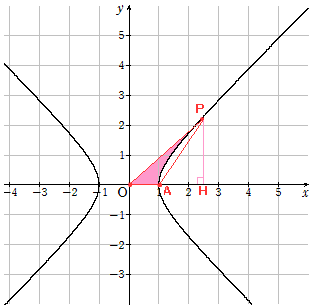（２）求める面積は、右図のピンク色の部分です。
△OPHから曲線とｘ軸と直線PHとで囲まれた
部分を引いて求めます。
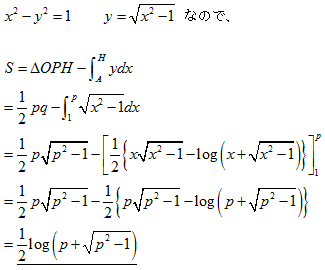
（３）（２）より、
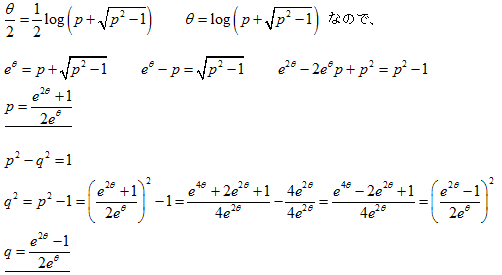
（４）
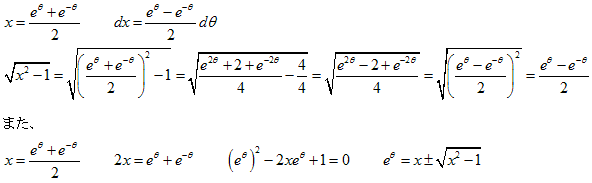
以上を踏まえて、
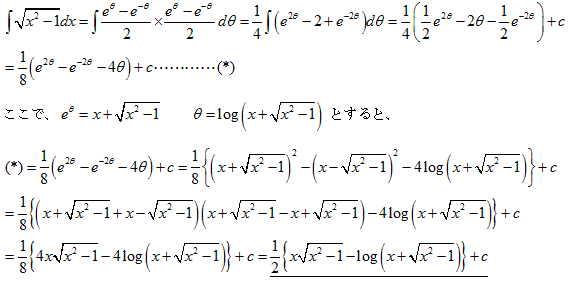
（５）次の式を踏まえて置換を考えます。
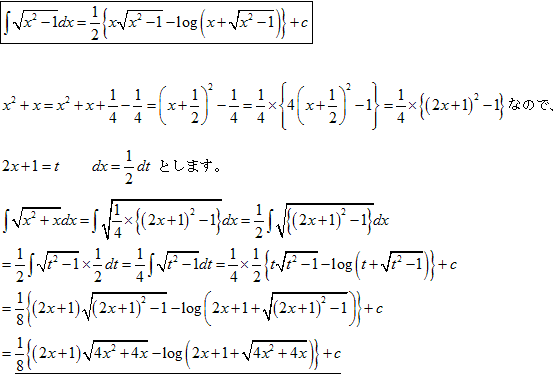
一部修正 8/9
コロキウム室NO1062にある問題
Ａ君は５５冊の漫画を１日１冊 (→*1日1冊以上)、合計３１日で読みました。
このとき、ある連続した何日かで丁度２５冊を読んでいることを示して下さい。
について、考えてみました。 ただし、連続した何日かというのは、「一日だけのときも含む」と考えるのでしょうかね。
一部修正 8/8
ｘｎ-1=0 (1)
を最初から複素平面状で考えます。
x=r( cosθ+i sinθ)
とおきます。(1)は
ｘｎ=rｎ( cos nθ+ i sin nθ) = 1 (2)
と書けます(ドモアブルでしたか、忘れたので加法定理で確認しました)
(2)が成り立つには
ｒ＝1
cos nθ＝1
i sin nθ＝0
よって
nθ＝2πｍ（ｍ＝0〜ｎ-1）
n=5の場合
θ＝0、2π/5、4π/5、6π/5、8π/5 となり
これを x=r( cosθ+isinθ) に代入すると解が得られます。
次に
ｘｎ-ａ=0
を考えます（ａは0では無い実数）
両辺をａで割り変形整理します
（ｘ/a 1/ｎ）ｎ-1=0
この後は上記解法によって同様に解き解にa 1/ｎをかけると解けます。
