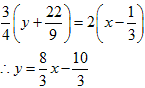NO.1946 相乗平均(2) 2011.6.26. 夜ふかしのつらいおじさん
NO.1945 相乗平均 2011.6.24. 数学マニア
複素平面上で考えたとき、「相加平均」 
はABの中点でよく知られていますが、
「相乗平均」 
（主値）は図形的にどの位置にあるでしょうか？
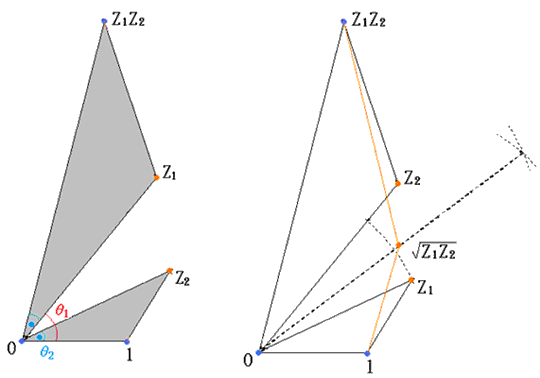
ColloquiumNO.270
|
図で表現すると、（１２時を０として、反時計回りに番号づけをして上の数から下の数へ矢印をつける）
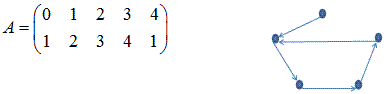
１と４を交換する。（ＡとＢを比較して、同じく3辺が集まっているところ）
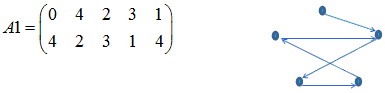
０と３を交換する。（Ａ１とＢを比較して、同じく矢印の始点になっている）
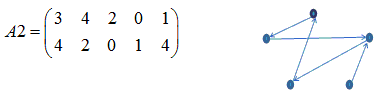
０と２を交換する。（Ａ２とＢを比較して、同じ形にする）
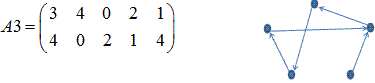
０と１を交換する。（Ａ３とＢを比較して、サイクルの向きを同じにする）
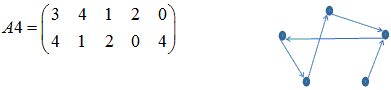
横に並びをそろえる。条件(1)より
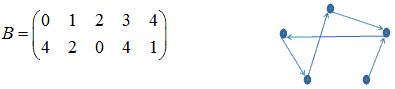
図形の特徴を、利用するとやりやすくなります。
例えば、以下の場合は不可能です。なぜなら、位相同型でないからです。
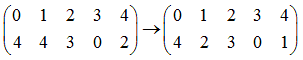
位相同型ならば、可能です。先の問題の場合
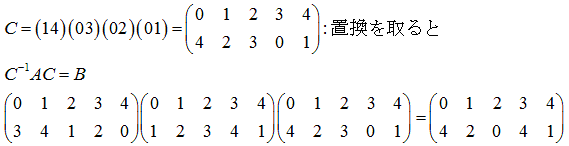
更に詳しくは、佐藤郁郎さんのホームページ上に載せて頂きました。
一般論としてまとめてありますので、興味ある方はご覧ください。
先週の解析学の授業でこのような問題がでました。
≪y=|x|は定義域を実数に持つ連続関数であることを示せ。≫
という問題なのですが、一応自分ではε-δ論法を使って下記のように回答しました。
ｘ＝0の時を考える。
ｆ(0)＝0より、lim_x→0 ｆ(x)＝0を示す。
任意のε>0に対して、あるδが存在して
|x|<δならば、|ｆ(x)−0|＝|X|＝|x|＜δ＜ε したがって連続である。
と回答したのですが、これではX＝0のときは成り立っても、
問題文中の「定義域を実数に持つ」という所に違和感を感じました。
これを回答する場合、どうすればいいでしょうか。
たぶん、ε−δ論法で証明していくと思うのですが、どうしたらいいでしょうか。
コロキウム室(リングセオリー・その３)を読ませていただき、少し疑問に思ったことがありましたので質問よろしいでしょうか？
（命題） PID内では（０）でない素イデアルは全て極大イデアルである
のとこの証明で、
そこでaとｂで生成されるイデアル（a、ｂ）を考えますと
とありますが、これはこの(a,b)が(a)を真に含む最小のイデアルであることを仮定しているのですか？
最終的にこの(a,b)がRに一致するので、Ωは極大イデアルということですが、
(a)⊂I⊂(a,b)
かつI≠RなるイデアルIが存在しないことがいえてないので、もしかしたらこのようなイデアルがあるかもしれません。
あるとすると、Ωの極大性が言えなくなってしまいますよね。
もし(a,b)が(a)を含む最小のイデアルであれば、確かに(a)が極大イデアルになりますね。
(a)を真に含む任意のイデアルがすべてRに一致するというのなら分かるのですが、具体的に(a,b)を持ってきた理由がよくわかりませんでした。
「大学への数学」のショートプログラムを読んでいたら面白い問題がありました。
紹介します。
問題１：単位円ｘ２＋ｙ２＝１と
円（ｘ−２）２＋（ｙ−３）２＝９の２つの交点を
Ａ，Ｂとするとき、直線ＡＢの方程式を求めよ。
問題２：円(1)：ｘ２＋ｙ２＝１、
円(2)：（ｘ−２）２＋（ｙ−３）２＝４とする。
点Ｐから円(1)，円(2)へ引いた接線の長さが等しくなるような点Ｐの軌跡の方程式を求めよ。
【参考】２つの円の方程式が分かっているとき、それらからｘ，ｙの2次の項を消去した式は、
直線を表し２つの円の根軸といいます。
問題３：ｘｙ平面上に、２つの放物線を
Ｃ１：ｙ＝ｘ２，
Ｃ２：ｙ＝−ｘ２＋４ｘ−２ とするとき、共通な接線の方程式を求めよ。
問題４：ｘｙ平面上に、２つの放物線を
Ｃ１：ｙ＝ｘ２，
Ｃ２：ｙ＝−ｘ２＋４ｘ−４
とする。
点Ｐから２つの放物線Ｃ１，Ｃ２へ引いた接線の長さが等しくなるような点Ｐの軌跡の方程式を求めよ。
(6月18日追加)
問題４を差し替え、改めて問題５とします。
問題５：ｙ＝ｘ２･･･(1) ｙ＝−ｘ２＋４ｘ−４・・・(2)と直線ｘ＝ｋの交点を
Ｐ，Ｑとする。
Ｐにおける(1)の接線とＱにおける(2)の接線の交点をＲとするとき、
Ｒの軌跡の方程式を求めよ。
ただし、軌跡の限界は求めなくて良い。
注：この記事に関する投稿の掲載は、2011年7月4日以降とします。
問題１（図でf=g(x)となっているのはｙ=g(x)と読みます）
２次関数を次のようにおきます
y=f(x)=2x2+ax+b・・・(1)
y=g (x)=-x2+cx+d・・・(2)
ここでグラフを平行移動しても比は変わらないのでＡを原点Ｏとするとb=d=0となります。
(1)(2)にこれを代入し連立でＢを求めると
((c-a)/3,(c-a)(2c+a)/9)が得られ、直線ＡＢはy=(2c+a)x/3となります。
次に直線ＣＥは、x=k (0＜k＜(c-a)/3) と書けます。整理すると
y=f(x)=2x2+ax・・・(3)
y=g (x)=-x2+cx・・・(4)
y=(2c+a)x/3・・・・・・(5)
x=k (0＜k＜(c-a)/3) ・・・(6)
Ｃ、Ｄ，Ｅのｙ座標は各々(6)と(4)(5)(3)連立して次のようになります。
Ｃｙ：-k2+ck
Ｄｙ：(2c+a) k/3
Ｅｙ：2k2+ak
ＣＤ：ＤＥ比は（Ｃｙ-Ｄｙ）/（Ｄｙ-Ｅｙ）なので
（-k2+ck -(2c+a) k/3）/（(2c+a) k/3-（2k2+ak））となり整理すると変数が全て消
え、ＣＤ：ＤＥ＝1/2＝1：2となります。
長々計算しましたが、実はこの種の問題では、Ｃ及びＥにおける増減量の問題で１
次、0次の項は無視してよいのは直感的に分かります。実務的には適度な一般化を自
在に駆使できると面白い問題となります。
例えばｎ次とｎ+ｐ次場合比はｐ-1次になりそうですが、きりがありませんのでやめます。
問題2
y=2x2のx=kとの交点における接線の方程式及び
y=-x2+4x-5のx=kとの交点における接線の方程式は次式で表され交点の軌跡はｋを消去すると得られる
k2-2kx +4x -y -5=0
k2-2kx +y/2 =0
y=2(4x-5)/3
ｋをパラメータとした2次関数の接線の交点の軌跡が1次関数になるのは直感的には納
得できます（接線が1次関数であり、それを創生する2次関数が2次の項を打ち消しあ
うことから）
しかし、交点の軌跡の係数と2次関数の導関数の一次の係数との関係が何かあるはず
で、この辺はもう少しほじくってみたいと思っています。
●準備
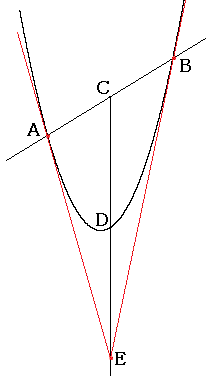
図のように放物線 y=ax2 に直線ABが交わっています。
放物線上の二点A(α,aα2) 、B(β,aβ2) における接線の交点をEとします。
Eから軸に平行な直線を引き図のようにC、Dとします。
直線ABの方程式は、
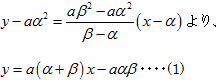
接線AEの方程式は、y - aα2 = 2aα(x-α)より、
y = 2aαx - aα2････(2)
同様に、接線BEの方程式は、
y = 2aβx - aβ2････（3）
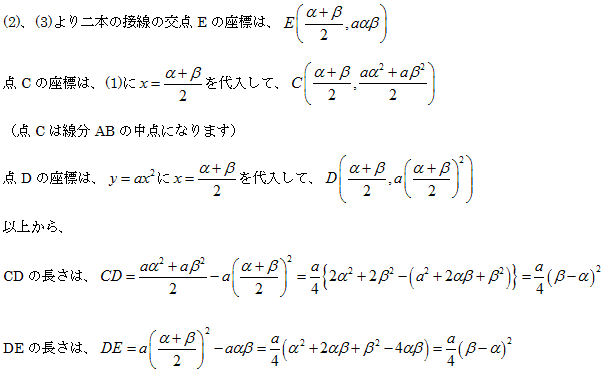
（CD＝DEとなります）
（この長さは、2乗の係数 a に比例します）
また、放物線と直線が囲む部分の面積は、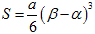
です。
（この面積も、2乗の係数 a に比例します）
問題１
●その１
図の青の部分と緑の部分の面積比は、1：2です。
このこととカバリエリの原理を考えると、CD：DE＝1：2です。
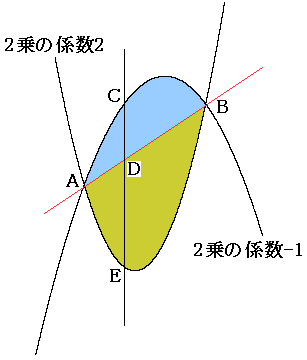●その２
上に開いた放物線の方程式を y = 2x2････(4)
下に開いた放物線の方程式をとりあえず
y = -x2+bx+c とします。
交点A、Bの x 座標が x = α,β となるように考えます。
2x2= -x2+bx+c
3x2-bx-c = 0
なので、この式が、
3(x-α)(x-β) = 0
3x2-3(α+β)x +3αβ = 0
となればよいので、
b = 3(α+β)
c = -3αβ
よって、下に開いた放物線の方程式は、
y = -x2+3(α+β)x-3αβ･･････(5)
直線ABの方程式は、式(1)において a=2 とすればよいので、
y = 2(α+β)x-2αβ です。
直線CEの方程式を とすれば、点C、D、Eの y 座標は、
C： -k2+3(α+β)k-3αβ
D： 2(α+β)k-2αβ
E： 2k2
よって、
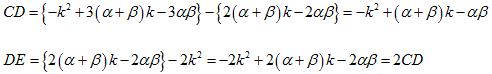
∴CD：DE＝1：2
問題２
●その１
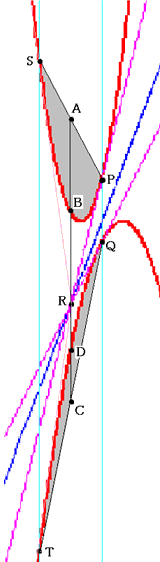ちょっと見にくいですが、二つの放物線の点Pと点Qにおける接線をピンクで表します。
その交点Rから二つの放物線に接線SR、RTを引きます。
点Rを通り軸に平行な直線を引きます。
（その線上の点を図のように、A、B、D、Cとします）
すると、線分SPの中点がA、線分TQの中点がCとなります。
そして、AB＝BR、CD＝DRです。
また、AB：CD＝2：1です。
以上から、BR：DR＝2：1です。
つまり、上下の放物線を軸に平行な線分で結んで
上の方から2：1に分ける点をつないだ線が求める答になります。
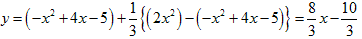
●その２
放物線 y = 2x2上の点Pにおける接線の方程式は、
y = 4kx-2k2
放物線 y = -x2+4x-5 上の点Qにおける接線の方程式は
y = (-2k+4)x+k2-5
これらを連立させて解くと、
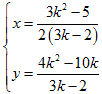
これらを割り算すると、
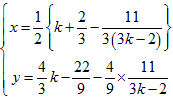
右辺の定数を左辺に移行して整理すると、
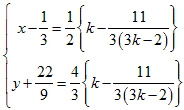
これから、
