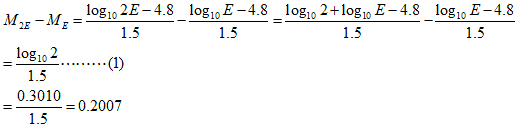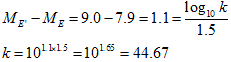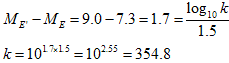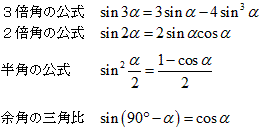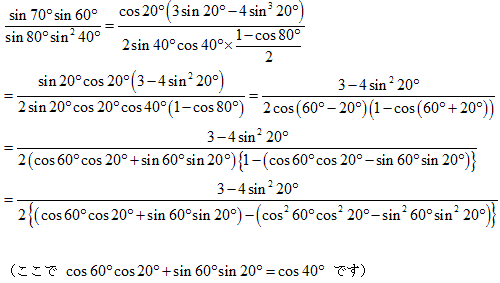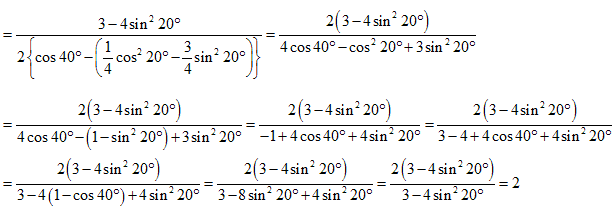NO.1926 東北地方太平洋沖地震によせて 2011.3.20. 夜ふかしのつらいおじさん
東北地方太平洋沖地震がおきました。
大変な出来事です。
実感を伴う理解はとてもできませんが、少しでもできることはしたいと思います。
ウィキペディアには、地震が発するエネルギーの大きさをE、マグニチュードをMとすると、
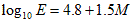
とあります。
この式によれば、
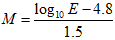 です。
です。
エネルギーEが2倍になると、
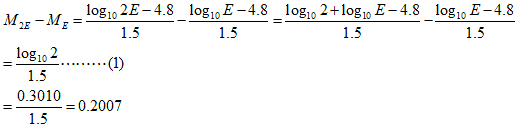
マグニチュードが約0.2増えるとエネルギーが2倍だということです。
((1)式の真数が何倍かを示しています)
関東大震災はマグニチュード7.9、東南海地震も7.9、
阪神淡路大震災は7.3とウィキペディアに載っています。
今回の地震はマグニチュード9.0だそうです。
関東大震災と比べると、
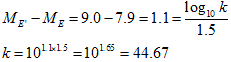
阪神淡路大震災と比べると、
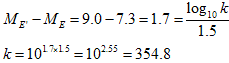
となります。
この値をどう考えればよいかわかりませんが、今まで日本が経験した地震よりも
ずっと広い範囲で大きな被害を受けたということだと思います。
心からお見舞い申し上げます。
NO.1925 3つの平方数の和 2011.3.14. 水の流れ
第255回数学的な応募問題
横浜国立大学の過去問から出題します。
(1)x2+y2+z2=nを満たす整数の組(x,y,z)
が存在しないような正の整数nを小さいものから順に6個求めよ。
(2)整数の2乗を8で割ったとき、余りとなる数をすべて求めよ。
(3)ここで、x2+y2+z2=nを満たす整数の組(x,y,z)
が存在しないような正の整数nについて、何か気がついたことがあれば考察せよ。
<出典から(3)は改題しました。>
注:この記事に関する投稿の掲載は、2011年4月4日以降とします。
NO.1924 格子点のこの角何度 (4) 2011.3.14. RYU1128
NO.1828 角度を求める問題(2)
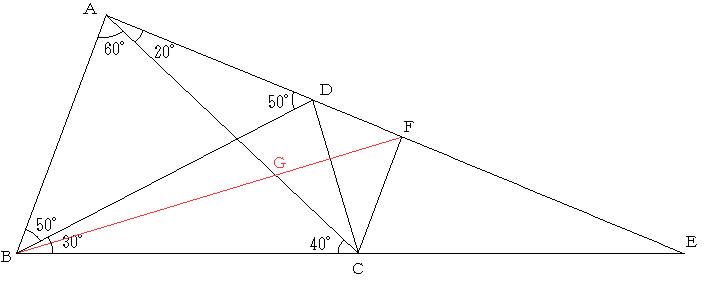
における四角形ABCDと本問における四角形ABCDは相似です。
故に角CADは20°となります。
NO.1923 格子点のこの角何度 (3) 2011.3.14. エルドス
答えは20°。幾何的に解けなかったので悔しいのですが、10進BASICで組みました。
CLEAR
OPTION ANGLE DEGREES
INPUT PROMPT "ABC=":abc
INPUT PROMPT "ACB=":acb
INPUT PROMPT "DBC=":dbc
INPUT PROMPT "DCB=":dcb
INPUT PROMPT "L=":l
LET ac=l*SIN(abc)/SIN(abc+acb)
LET dc=l*SIN(dbc)/SIN(dbc+dcb)
LET ad=(ac*ac+dc*dc-2*ac*dc*COS(dcb-acb))^0.5
LET dac=ACOS((ad*ad+ac*ac-dc*dc)/(2*ad*ac))
PRINT "DAC=";dac
END
実行結果
ABC=80
ACB=40
DBC=30
DCB=70
L=1
DAC= 19.9999999999999
NO.1922 格子点のこの角何度 (2) 2011.3.14. 夜ふかしのつらいおじさん
●準備として、次の公式を確認しておきます。
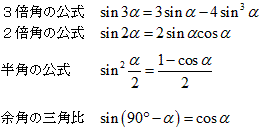
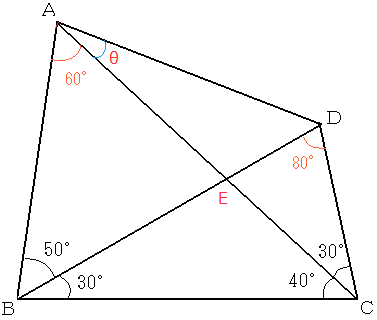
●下の図でAB=1、∠CAD=θ、対角線ACとBDの交点をEとします。
方針は、△ABDが二等辺三角形をいいます。
すると∠ADB=50°になり、θ=20°が導かれます。
●三角形の内角の和が180°であることを用いて∠BAC=60°、∠BDC=80°はすぐにわかります。

●次に(1)式の( )の中の式が0になることを調べます。
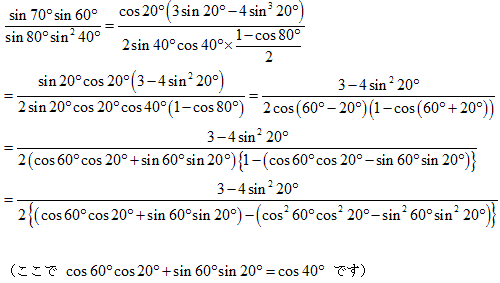
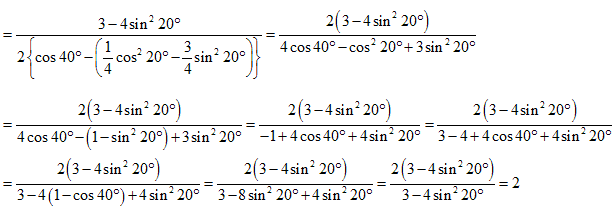
となり、AD=1より△ABDは二等辺三角形になり方針の通りになりました。
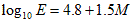
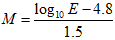 です。
です。