Weekend Mathematics／コロキウム室／1998.7～12／NO.26

コロキウム室

NO.202 　　　 11/15 　　 Junko 　　　 長方形の問題（６）

「Ｎ段ある階段を１段ないし、２段づつ登るとき、 その登り方の総数Ｓｎはいくつでしょう？」
この問題の答えもフィボナッチ数列です。
Ｎ段ある階段の最後の段階を考えます。
(Ｎ－２)段目から、最後２段進んで登り切るか、 (Ｎ－１)段目から、最後１段進んで終わるかのいずれかになります。
従って、Ｓｎ＝Ｓｎ－２＋Ｓｎ－１ という漸化式がなりたちます。
Ｓ１＝１、Ｓ２＝２ですから、 フィボナッチ数列に他なりません。

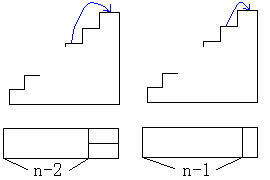
これを、前回の長方形の敷き詰め問題に対応させて考えることもできます。
左の図のように最後の段階で、階段を２段登るというのは、 長方形を横に２つ並べることに対応させます。
また階段を１段登るということは長方形を縦に置くことに対応させればいいわけです。





NO.203 　　　 11/16 　　　 水の流れ 　　 大相撲本場所（３）

Junkoさんは○を間に入れておられましたが、 組み合わせのＣに持ち込むこともできます。
すなわち、×（負けの数）で場合分けします。 （でも、同じ考えですが）
×をｋ個（ｋ≧０）のとき、○（１５－ｋ）個です。
ただし、ｋ≧９のときは、明らかに不適。

  1. ｋ＝０のとき、○のみで１通り
  2. ｋ＞０のとき、×の起こりうる日は○両端及び間の
    　　　　１５－ｋ＋１＝１６－ｋ
    　　　よって、×の起こる日は16-kＣk（ｋ＝１，２，３，・・・，８）
したがって、その総数は 
　１＋15Ｃ1＋14Ｃ2＋13Ｃ3＋12Ｃ4＋・・・＋9Ｃ7＋8Ｃ8

＝１５９７
となります。



NO.204 　　　 11/18 　　 海津北高校情報処理科２年　　　 長方形の問題（７）

数学の時間に考えた問題の解答を送ります。 

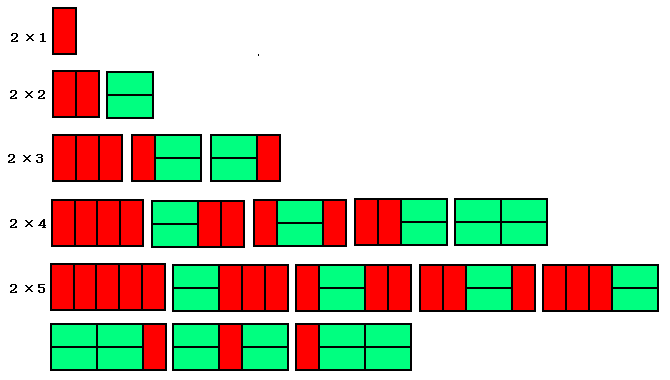
２×１・・・１
２×２・・・２
２×３・・・３
２×４・・・５
２×５・・・８
・・・
となっているので、２×ｎ（ｎ＞２）の長方形の場合は ２×（ｎ－１）の場合の答えと２×（ｎ－２）の場合の答えを 合計したものになります。
このような数列をフィボナッチ数列と呼ぶそうです。 身近なものにこのような数列が隠されていて とても驚きました。



NO.205 　　　 11/18 　　 Junko 　　　 獅子座流星群

今朝、ピ－クを迎えたという獅子座流星群をご覧になりましたか？
私は午前３時から４時半位まで、東の空を眺めました。 空は晴れ渡っていて、観察には絶好のコンディションでしたが、 何せ横浜の空は明るすぎて・・・。 それでも大小合わせて２０個以上は見たかな？　 それはそれは、素敵な光景でした。
こんなにじっくりと夜空を眺めるなんて、本当に久しぶりです。 流星群とは別に、改めて地球は自転しているのだなあと感じました。 星の位置がずれていく（天の北極を中心に回転している）んですもの。



NO.206 　　　 11/19 　　水の流れ 　　　 ジュ－スの問題（５）

先日のジュースの問題の一般の場合を書きます。

命題：ｓ，ｔが最大公約数（ｓ，ｔ）＝１を満たす自然数であるとき、 いくつかのｓといくつかのｔの和として表せない最大の自然数は ｓｔ－ｓ－ｔである。

＜証明＞

  1. （ｓ，ｔ）＝１のとき、ｓとｔの最小公倍数はｓｔであるから、
    「ａｓをｔで割ったときの余りが１であるような自然数ａ（１≦ａ≦ｔ） が存在する」
    ことを示す。

    この証明：
    ０×ｓ，１×ｓ，２×ｓ，・・・，（ｔ－１）ｓ 　のｔ個のをｔで割ったときの余りを全部調べて １が出てこなかった場合は、 残り（ｔ－１）種類の余りのうち２回以上出てきたものがある。 もし、ｅｓとｆｓとの余りが等しいなら、
    　 ｆｓ－ｅｓ＝（ｆ－ｅ）ｓ＜ｔｓ
    となり、ｔで割った余りが０で、形からみるとｓでも割り切れる。
    これは、ｓとｔの最大公約数がｓｔに反する。
    だから、ｔで割ったときの余りが１であるようなａｓ（１≦ａ≦ｔ）が存在する。

  2. したがって、ａｓをｔで割った商をｂで表すと、 ａｓ＝ｂｔ＋１で、ａｓ－ｂｔ＝１ となる。
    さて、任意の自然数ｎに対して、
    ｎ＝ｎ（ａｓ－ｂｔ）＝ｎａ×ｓ－ｎｂ×ｔが成り立つ。
    ここで、－ｎｂが負の整数なのでｓの係数をｔだけ減らすと同時に、 ｔの係数ををｓだけ増やしていく （ｓｔ－ｔｓ＝０だから良いわけです）。
    ｓの係数がマイナスになる前にｔの係数が０以上になれば、 ｎがｓとｔの和として表される。
    そうでないときは、ｎ＝ｕｓ－ｖｔ であって、 次ぎに、ｎ＝（ｕ－ｔ）ｓ＋（ｓ－ｖ）ｔ
    ただし、１≦ｕ≦ｔ－１，ｖ≧１である。
    故に、ｎ＝ｕｓ－ｖｔ≦（ｔ－１）ｓ－１×ｔ＝ｓｔ－ｓ－ｔ となるから、ｓとｔとの和で表すことのできない最大の自然数は 　ｓｔ－ｓ－ｔである。＜証明終わり＞




NO.207 　　　 11/19 　　　 水の流れ 　　 大相撲本場所（４）

大相撲の問題と２×ｎの長方形は同じ結果なのです。初項違いで。



NO.208 　　　 11/21 　　　 Junko 　　 大相撲本場所（５）

これもフィボナッチ数列なのですか？　ええ－っ、驚き！　
検証してみます。 Ｎ試合するとして、連敗(２連敗以上)しない、勝ち負けの勝敗の起こり方が ｆ(Ｎ)通りとします。
NO.201で確かめた結果から、 ｆ(１５)＝１５９７とかけるわけですよね。

Ｎ＝１から順に確かめてみます。

  • Ｎ＝１
    「○」か「×」の２通り。ｆ(１)＝２
  • Ｎ＝２
    「○○」「○×」「×○」の３通り。ｆ(２)＝３
  • Ｎ＝３
    「○○○」「○○×」「○×○」「×○○」「×○×」の５通り。ｆ(３)＝５
  • Ｎ＝４
    「○○○○」「○○○×」「○○×○」「○×○○」
    「×○○○」「×○×○」「×○○×」「○×○×」の８通り。ｆ(４)＝８
確かにフィボナッチ数列のような雰囲気・・・。
フィボナッチ数列を定義づけている漸化式、 ｆ(Ｎ－２)＋ｆ(Ｎ－１)＝ｆ(Ｎ)に代入してみると、
ｆ(５)＝１３、ｆ(６)＝２１、ｆ(７)＝３４、 ｆ(８)＝５５、ｆ(９)＝８９、ｆ(１０)＝１４４、 ｆ(１１)＝２３３、ｆ(１２)＝３７７、ｆ(１３)＝６１０、 ｆ(１４)＝９８７、ｆ(１５)＝１５９７ というわけで、確かに先程の結果と一致します。
う－ん、としばらく考えて・・・
なるほど連敗(２連敗以上)しないということは、 次の２つのケ－スがあるということに思い至りました。
１つは、(Ｎ－１)試合目までがどうであれ、Ｎ試合目に勝てばいいわけです。
もう１つはＮ試合目に負ける場合ですが、 これは(Ｎ－１)試合目が勝った場合にのみ許されるわけです。 この時、(Ｎ－２)試合目までの勝敗は問いません。

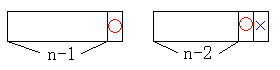つまりこの場合もまた確かに、
ｆ(Ｎ－２)＋ｆ(Ｎ－１)＝ｆ(Ｎ)が成立しているのです。

この問題をNO.201では、組み合わせ(Combination)を使って解きました。 ということは、フィボナッチ数(フィボナッチ数列に登場する数をこう呼びます。)は、 必ず組み合わせ(Combination)の和として表せるということなのでしょうか？



NO.209 　　　 11/21 　　　ありさのお父さん 　　 Alphabetの問題・Part2（１）

私からも類似問題を。
ちょっとルールが違っていて， ２回以上同じアルファベットがでてきますが。

Ｏ，Ｔ，Ｔ，Ｆ，Ｆ，□，△，....

ヒント：□と△は同じものが入ります。








E-mail 戻る