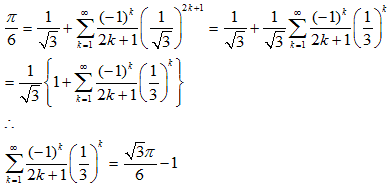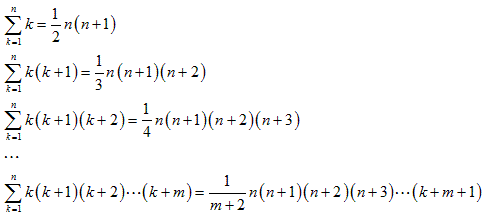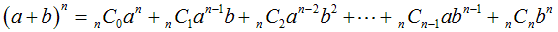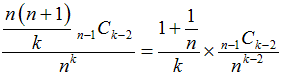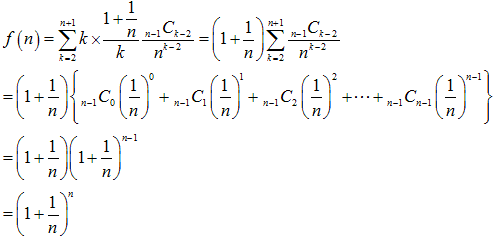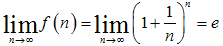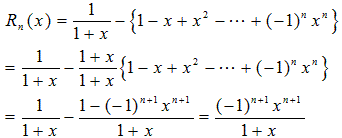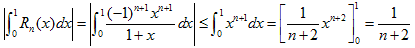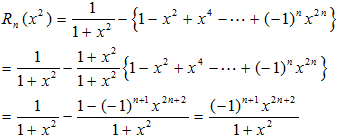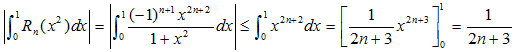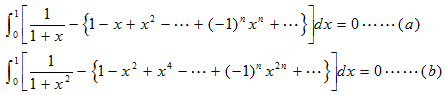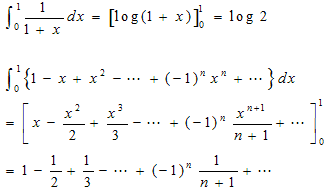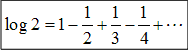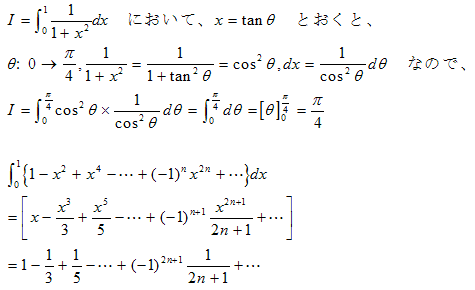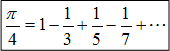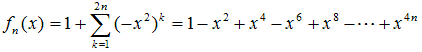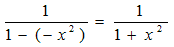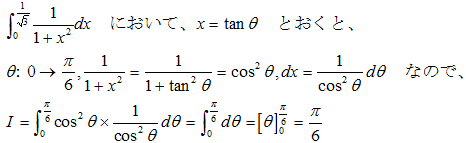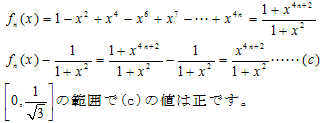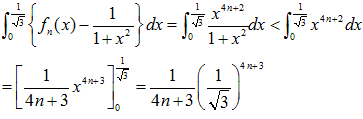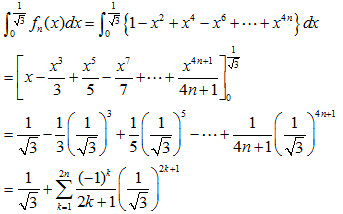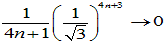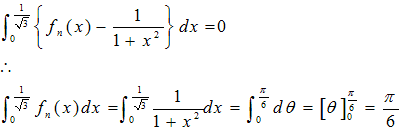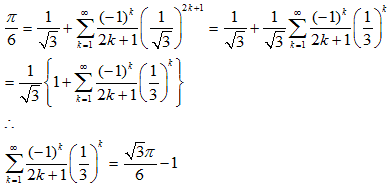NO.1844 自然対数と確率 2010.3.29. 水の流れ
第239回数学的な応募問題
確率の問題を見ていると、その結果に驚く場合があります。次の問題を考えてください。
問題1:一つのサイコロを繰り返し振って、出た目の和が6を超えるまで振り続ける。
サイコロを振る回数の期待値を求めよ。
問題2:1からnまでの自然数を一つずつ書いたカードが計n枚あって、そこから無作為に1枚抜き取っては元に戻す。抜き取ったカードに書かれた数の和がnを超えるまで繰り返すとき、カードを抜き取る回数の期待値をEnとする。
nを無限大にしたとこのEnの極限値を求めよ。
<水の流れ:詳細な解答には至っていませんが>
注:この記事に関する投稿の掲載は、2010年4月19日以降とします。
NO.1843 有名ないい話(2) 2010.3.29. 夜ふかしのつらいおじさん
(0)
事前に次の式を確認しておきます。
1.連続する自然数の積からできている数列の和の式(数学的帰納法で簡単に確認できます)
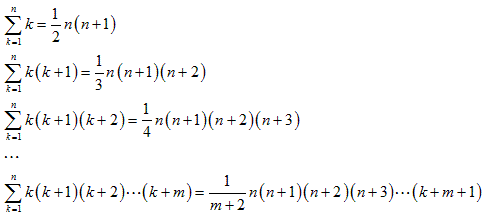
2.二項定理
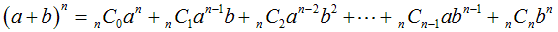
(1)
k回目に直前のカードの数以下の数のカードを出す場合の数を数えます。
k−1回目までは数が増え続けます。
k回目はk−1回目に出たカードの数と同じだけの場合の数があります。
k−1回目のカードの数は、k−1からnまでの場合があります。
その直前のk−2回目のカードの数は、k−1回目より1だけ少ないk−2からn−1の場合があります。
k−2回目までの数の並べ方の場合の数は、
最小のときは、1からk−2のk−2個の数の中からk−2個の数を組み合わせる
k-2Ck-2と同じです。
最大のときは、1からn−1のn−1個の数の中からk−2個の数を組み合わせる
n-1Ck-2と同じです。
k−1回目のカードの数をmとします。(mは、k−1からnまでの場合があります)
以上から得点がkとなる場合の数は、

よって得点がkとなる確率は、k回カードを取り出すとnk通りの場合があるので
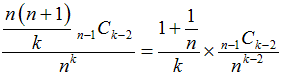
(2)
期待値f(n)の計算は、
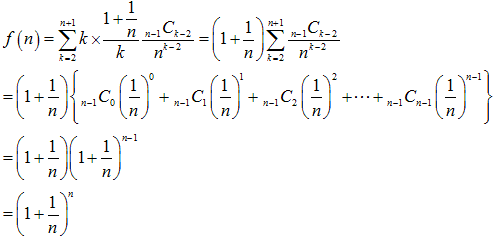
よってその極限値は、
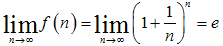
NO.1842 有名ないい話 2010.3.8. 水の流れ
第238回数学的な応募問題
2005年に東北大学の入試問題は結果がいい話になる有名な問題でした。
ここに紹介します。

注:この記事に関する投稿の掲載は、2010年3月29日以降とします。
NO.1841 有名な無限級数(2) 2010.3.8. 夜ふかしのつらいおじさん
札幌医科大学
(1)まず、Rn(x)を変形します。
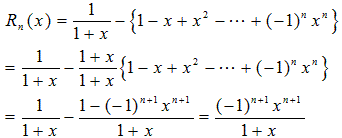
積分区間が、[0,1]なので次の不等式が成り立ちます。
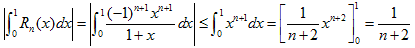
次に、Rn(x2)について考えます。
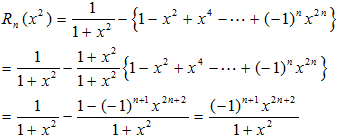
積分区間が、[0,1]なので次の不等式が成り立ちます。
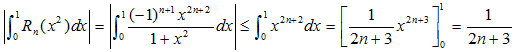
(2) (1)において、n→∞のときRn(x)もRn(x2)も0に収束します。
つまり、n→∞のときには、
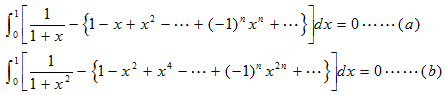
(a)の両辺を別々に積分すると
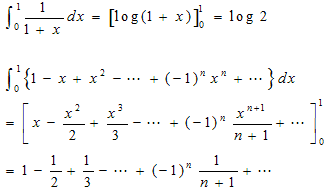
よって
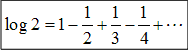
(b)の両辺を別々に積分すると
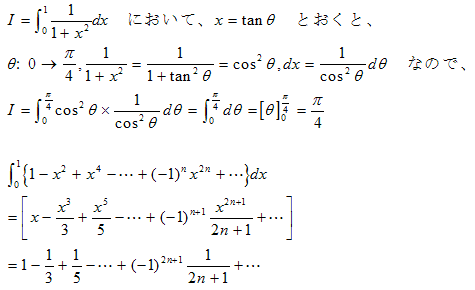
よって
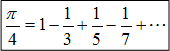
同志社大学
(1)
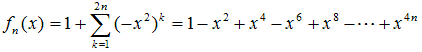
これは、初項1、公比(−x2)の等比数列(公比の絶対値は1より小さい)なので、
n→∞なら、無限等比級数になるので、fn(x)は、次の式に収束します。
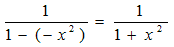
(2) 札幌医科大学の(2)の(b)の積分でθ:0→π/6となればよいので
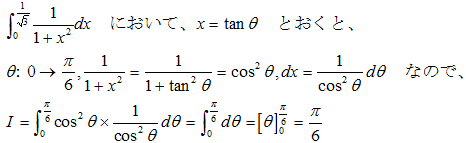
(3)
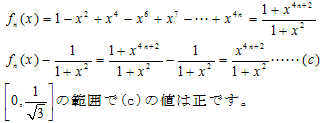
だから積分の値も正になります。
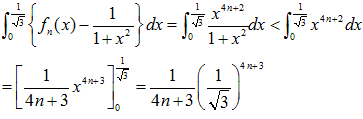
(4)
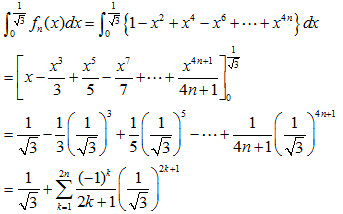
(5) (3)の右辺はn→∞のとき0に収束します。
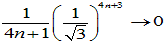
だから、n→∞のとき、
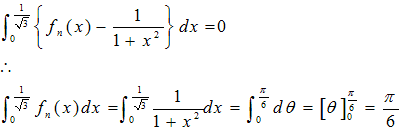
これと(4)の結果とを比べて(n→∞のとき)