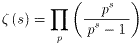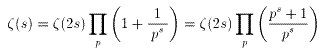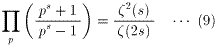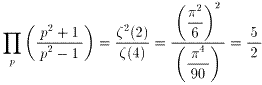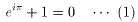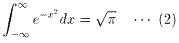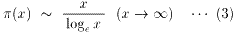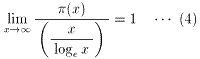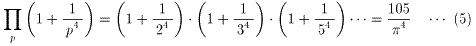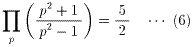NO.1807 ラマヌジャンの無限積、その証明(2) 2009.9.28. スモークマン
NO.1804ラマヌジャンの無限積、その証明
は...わたしは以下のように考えました...
これらの式は...ζ(8) とζ(4) がわかれば出せますよね...^^
http://www5b.biglobe.ne.jp/~sugi_m/page031.htm より
ζ(n)の具体的数値
ζ(n)の値を感覚的に把握してもらうために、具体的数値を示しておきましょう。
定義式 ζ(s)=1+1/2s+1/3s+1/4s+1/5s+・・・・・より、
ζ(2)=1+1/22+1/32+1/42+・・・・ =π2/6=1.64493・・
ζ(4)=1+1/24+1/34+1/44+・・・・ =π4/90=1.08232・・
ζ(6)=1+1/26+1/36+1/46+・・・・ =π6/945=1.01734・・
ζ(8)=1+1/28+1/38+1/48+・・・・ =π8/9450=1.00481・・
上の事実を使えば...
ラマヌジャンの最初の公式 (a) は...
1/ζ(8)=(a)*1/ζ(4)
(a)=ζ(4)/ζ(8)=(π
4/90)*(9450/π
8)=105/π
4
と出せますね♪
あとの公式 (b) も上と同様に...
ζ(2)/ζ(4)=(π
2/6)/(π
4/90)=15/π
2
(b)=(15/π
2)*(π
2/6)=5/2
NO.1806 累乗和の求め方 2009.9.24. 水の流れ
第230回数学的な応募問題
先日、「大学への数学8月号」を読んでいたところ、累乗和の求め方の記事があり、
今までと違った方法でしたので、紹介を兼ねて出題します。

注:この記事に関する投稿の掲載は、2009年10月12日以降とします。
NO.1805 開票経過(2) 2009.9.24. 夜ふかしのつらいおじさん
問題1
Aが5個、Bが3個あるときの同じ物がある場合の順列を考えて、
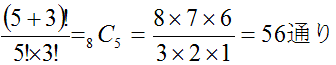
問題2
A候補の得票が終始B候補の得票を上回る事象の余事象は、B候補が開票途中でA候補と同数かA候補を上回ることです。
そうなる場合を考えると、
(1)1票目がBの場合
残り、A5票、B2票の順列を考えて、
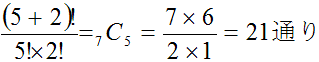
(2)2票目までがABの場合
残り、A4票、B2票の順列を考えて、

(3)4票目までがAABBの場合
残り、A3票、B1票の順列を考えて
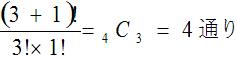
(4)6票目までがAAABBB,AABABBの場合
残り、A2票の順列を考えて
2×1=2通り
ゆえに、
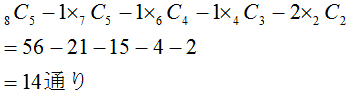
問題3
Aがa個、Bがb個あるときの同じものがある場合の順列を考えて、
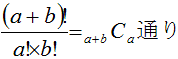
問題4
具体的にいくつか考えます。
(1)A2票、B1票の場合は、AABの場合しかないので、
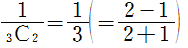
(2)A3票、B1票の場合は、AAAB,AABAの2通りしかないので、
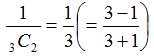
(3)A5票、B3票の場合は、問題1、問題2より、
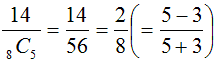
・・・
以上から、 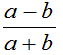 と推測されます。
と推測されます。
さて、Aがa票,Bがb票の場合、Aの得票が常にBの得票より多い確率を
 と仮定します。
と仮定します。
合計が1票増える場合を考えます。
考え方の要点は、最後の票がAでもBでもその手前の(a+b)票目までと様子が変わらないことです。
(1)Aが1票増える場合
a)最後がAの場合
このときは、Aがa票、Bがb票の場合を考えます。
Aが常にリードする場合の数は、
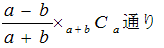
b)最後がBの場合
このときは、Aが(a+1)票、Bが(b-1)票の場合を考えます。
Aが常にリードする場合の数は、
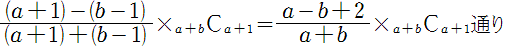
ゆえに求める確率は、
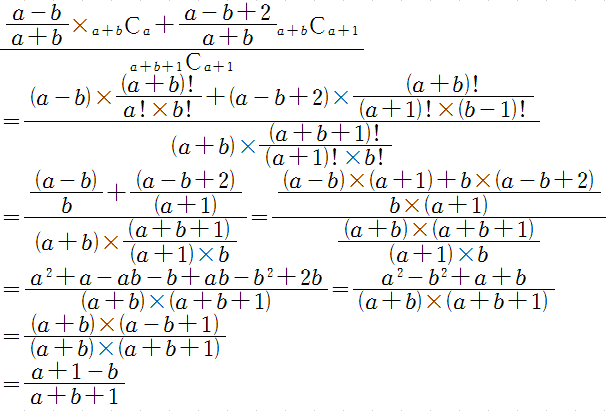
(2)Bが1票増える場合
a)最後がAの場合
このときは、Aが(a-1)票、Bが(b+1)票の場合を考えます。
Aが常にリードする場合の数は、
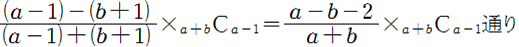
b)最後がBの場合
このときは、Aa票、Bb票の場合を考えます。
Aが常にリードする場合の数は、
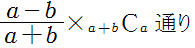
ゆえに求める確率は、
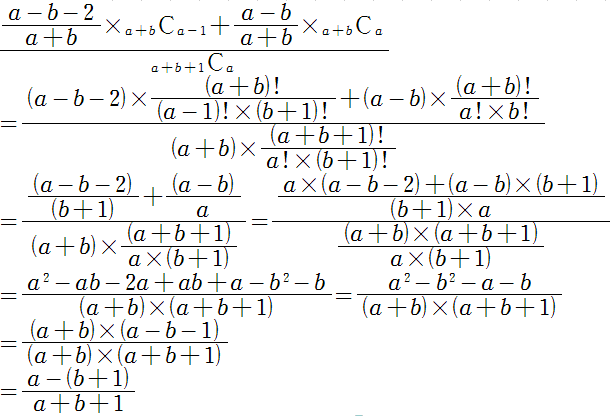
以上より成立するといえます。
考察
ずっとA候補者の得票がB候補者の得票を上回る開票経過は、
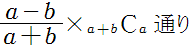
NO.1804 ラマヌジャンの無限積、その証明 2009.9.15. K.F.
NO.1798ラマヌジャンの連分数には、手も
足も出ませんでしたが、NO.1803 (5)、(6)は、証明できました。以下、証明を述べます。
1.  (pは素数)の証明
(pは素数)の証明
(方針)Riemann のζ関数とその Euler 積としての表現(1)を利用する。
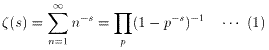
(1)の証明
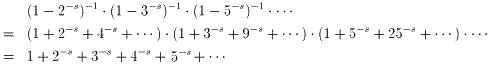
より(1)が成り立つ。
注) 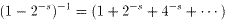
他の式は、等比級数の和の公式(s>0、p>1より、0<p-s<1)から、
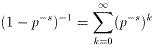
が成り立つから正しい。具体的には、
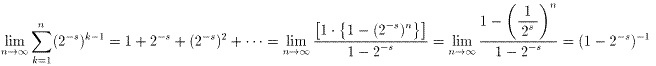
他の素数(3,5,7・・・)に対しても、上記のことが同様に成り立つ。
(証明終わり)
(1)から、
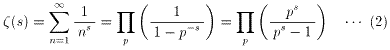
となる。したがって、
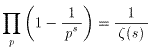
となるから、
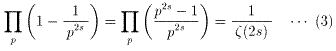
となる。一方、
p2s-1=(ps-1)(ps+1) ←→
p2s=1+(ps-1)(ps+1)・・・(4)
が成り立つので、(4)を(3)に代入すると、
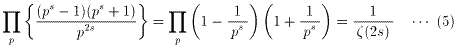
となる。(5)を変形すると、
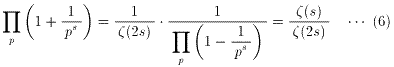
を得る。sが任意の正の偶数のときのζ(s)の値は、
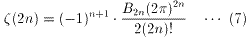
で表されることがわかっている(ここで、Bnは、Bernoulli 数)から、
(7)にn=2、n=4を代入すると、

だから、
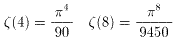
を得る。得られたζ(4)、ζ(8)の値を(6)に代入すると、
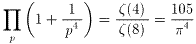
となる。
(証明終わり)
2. 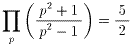 (pは素数)の証明
(pは素数)の証明
(2)と(6)より、
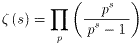
と、
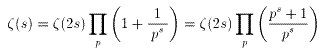
が得られる。これらの式を掛け合わせると、

となる。(8)を変形すると、
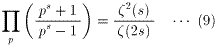
を得る。(9)にs=2を代入すると、
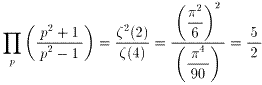
となる。
(証明終わり)
このように証明してみると、今まで不思議だったp(素数)とπとの関係が
当然のように思えてきます。
NO.1803 eとπとp(素数)、それらの間の密接で不思議な関係 2009.9.1. K.F.
eとπとp(prime number:素数)との間には、密接で不思議な関係があります。
一つ一つ確かめていきましょう。
1.eとπ
これら二つの数、数学の中で古くから知られている特別でしかも
重要な定数ネイピア数(自然対数の底)e と円周率πに深い関係が
あることは、理工系の大学生なら知っています。例として、
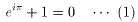
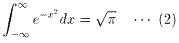
などがあげられます。
(1)は、オイラーの等式、(2)はガウス積分として知られています。
どちらも証明は簡単です。
ただ、(2)は二重積分を解かなければならないので少し厄介です。
2.eとp
eと、数学的に見てもっとも興味ある数のグループであるp(素数)にも
密接で不思議な関係があります。
π(x)は、x以下の素数の個数を表す関数として、
「素数の個数関数」といわれていますが、次の式が成り立つことが知られています。
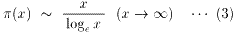
ここで、「~」は、漸近的に等しいという意味で、式で書けば、
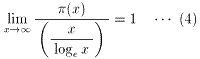
となります。
(3)、(4)は、「素数定理」と言われています。
ガウスが初めて予想してから約100年かかって証明されました。
このことだけでも、この定理の証明が難しいことがわかると思います。
理工系の数学が好きな大学生なら知っていますが、いざ証明するとなると
非常に難しく、複素関数論を学び直し、ζ関数理論とDirichletのL関数理論を勉強して、
やっと証明が理解できました。
証明は、『数論Ⅰ』(岩波書店、2005年)などに載っています。
数論を愛する方は、ぜひチャレンジしてみてください。
3.πとp
eは、「自然」対数の底なので、eとpに密接な関係があることに
納得された方も、πとpに密接な関係があるといわれると驚かれるのではないでしょうか。
それがあるのです。
大学院の図書館で見たラマヌジャンの全集に、
その好例が載っていました。
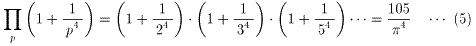
です。ラマヌジャンは他にも、πとは直接関係ありませんが、次のような無限積も残しています。
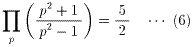
4.以上のことから、e、π、p相互の間に深くて、密接で不思議な関係が
あることがわかりました。すなわち、
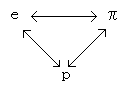
このようなことを知ると、数学がますますおもしろくなると思います。

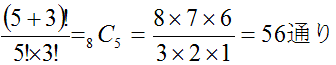
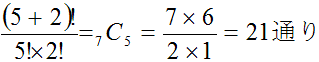

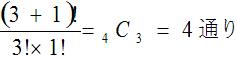
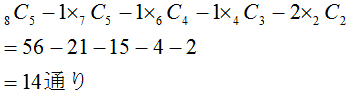
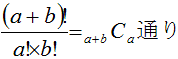
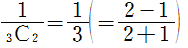
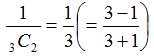
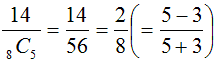
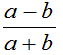 と推測されます。
と推測されます。 と仮定します。
と仮定します。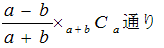
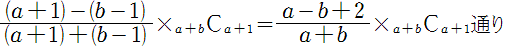
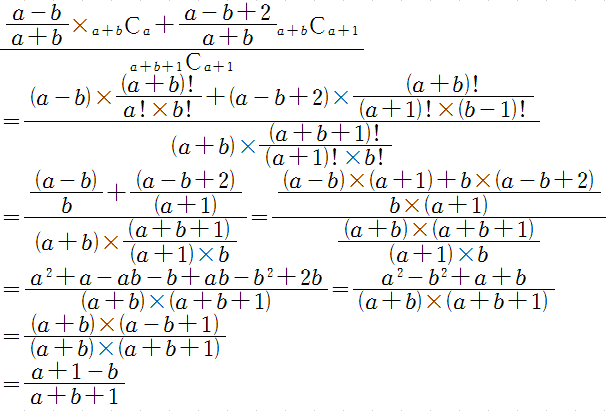
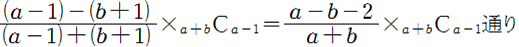
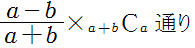
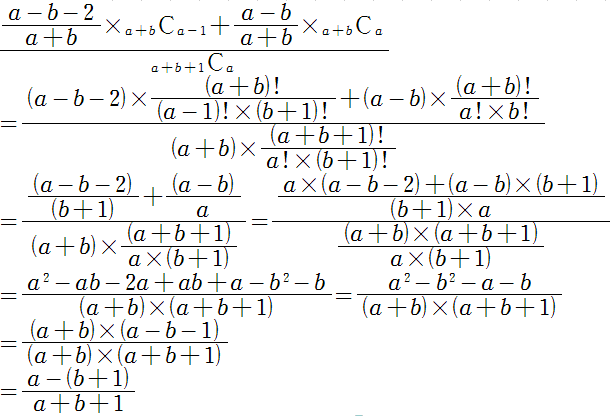
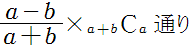
 (pは素数)の証明
(pは素数)の証明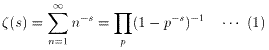
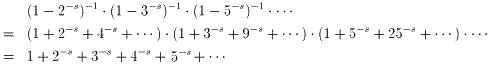
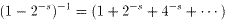
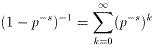
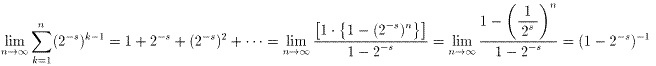
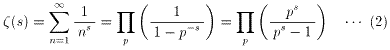
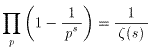
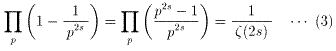
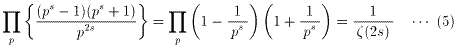
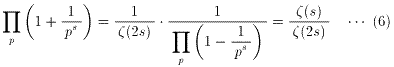
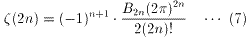

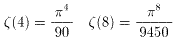
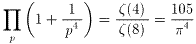
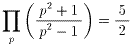 (pは素数)の証明
(pは素数)の証明