NO.1802 開票経過 2009.8.24. 水の流れ
第229回数学的な応募問題
皆さん!衆議院総選挙が、8月30日に行われます。そこで、選挙の問題を考えました。
A,Bの二人が立候補したある選挙区は大激戦でして、1票ごとの開票経過が気になります。
開票経過の起こりうる方法はすべて同じとする。
問題1:A候補者が5票で、B候補者が3票のとき、一票ごとの起こりうる開票経過は何通りあるか求めよ。
問題2:A候補者が5票で、B候補者が3票のとき、一票ごとの開票中ずっと
A候補者の得票がB候補者の得票を上回る確率を求めよ。
問題3:A候補者がa票で、B候補者がb票のとき、一票ごとの起こりうる開票経過は何通りあるか求めよ。
問題4:A候補者がa票で、B候補者がb票のとき、一票ごとの開票中ずっと
A候補者の得票がB候補者の得票を上回る確率を求めよ。ただし、a>bである。
考察: A候補者がa票で、B候補者がb票のとき、一票ごとの開票中ずっとA候補者
の得票がB候補者の得票を上回る開票経過は何通りあるか、可能なら考えてください。
注:この記事に関する投稿の掲載は、2009年9月21日以降とします。
NO.1801 出口調査(2) 2009.8.24. 夜ふかしのつらいおじさん
投票者がAに入れる確率をp、Bに入れる確率をqとします。(p+q=1)
投票者がn人いるとすると、候補者Aがk票獲得する確率f(k)は、
f(k)=nCk pkqn-kとなります。
((p+q)nの展開のpについてk次の項)
候補者Aの獲得票数の期待値は、
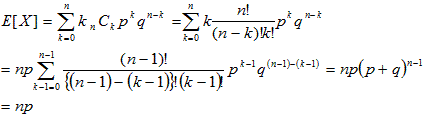
候補者Aの獲得票数の分散は、
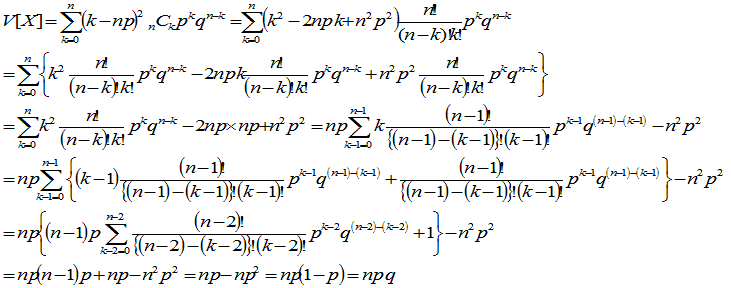
さて、npがある程度大きいとき(資料により5とか10とかの記述があります。
この場合は1000×0.5=500程度です)
次の変数は、正規分布N(0,1)にほぼ従うとみて良いようです。
XはAの獲得人数です。
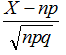
正規分布表によると、この値が95%の範囲に入るのは、
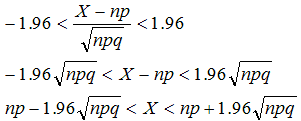
結果1の場合、n=1000、p=0.55、q=0.45なので、Aの獲得投票数は、
519人から581人
となりと当選します。
結果2の場合、n=1000、p=0.53、q=0.47なので、Aの獲得投票数は、
499人から561人
となりと95%の信頼度では当選しない場合もあります。
Aが95%の信頼度で確実に当選するには、
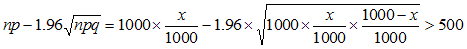
の不等式を解いて、x=531人です。
この場合、n=1000、p=0.531、q=0.469なので、Aの獲得投票数は、
500.1人から561.9人
NO.1800 正三角形であることの証明(3) 2009.8.16. K.F.
NO.1790 正三角形であることの証明について、
別解が見つかりましたので、お知らせします。
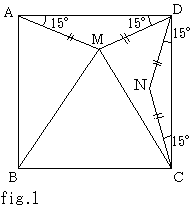
まず、∠NDC=∠DCN=15°となるように、点Nを定める。(fig.1)
すると、△AMD≡△DNCで、かつそれぞれの三角形は二等辺三角形となる。(ND=NC)
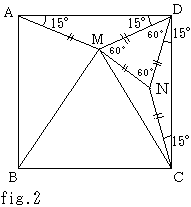 さらに、∠MDN=60° かつMD=NDとなるので、△DMNは正三角形であることがわかる。(fig.2)
さらに、∠MDN=60° かつMD=NDとなるので、△DMNは正三角形であることがわかる。(fig.2)
故に、∠MDN=∠DMN=∠DNM=60°であり、かつMD=ND=NMとなる。
そして、△DNCは二等辺三角形だから、ND=NC=NMが成り立つ。
なおかつ、∠DNC=∠MNC=150°となるから、三角形の合同の定理
「二辺とそのはさむ角がそれぞれ等しければ、それらの三角形は合同である。」より、
△AMD≡△DNC≡△MNCとなる。
故に、AD=DC=MC
fig.2の左半分についても、同様にして、AD=AB=MBが成り立つ。
最後に四辺形ABCDは正方形だから、MC=MB=BC
したがって、△MBCは正三角形である。 (証明終わり)
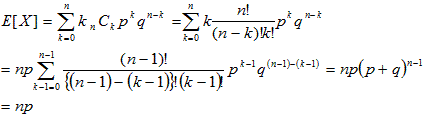
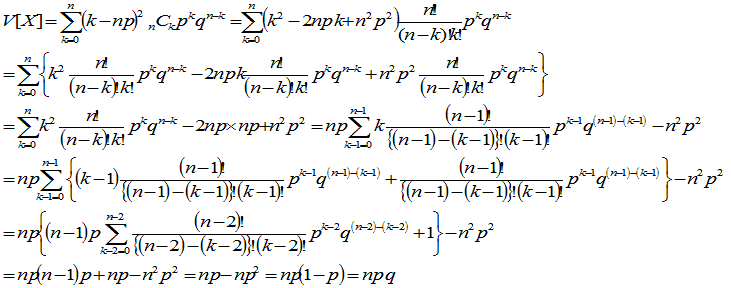
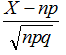
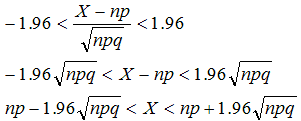
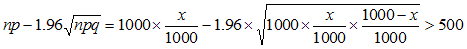

 さらに、∠MDN=60° かつMD=NDとなるので、△DMNは正三角形であることがわかる。(fig.2)
さらに、∠MDN=60° かつMD=NDとなるので、△DMNは正三角形であることがわかる。(fig.2)