Colloquium

NO.1793　　　ある漸化式　　2009.6.15.　　水の流れ

第２２６回数学的な応募問題

皆さん、先日大学入試問題を眺めていたら、上智大学の過去問から次のような漸化式を見つけました。 チャレンジください。

注：この記事に関する投稿の掲載は、2009年7月6日以降とします。

NO.1792　　　　数値が交替する連続根号数　　2009.6.15.　　K.F.

「数値が交替する連続根号数」についての進捗状況について報告します。
まず、最も単純な例として、

　

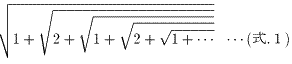
について考えました。この場合も、連立方程式

　

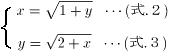
を考えます。(式．２)に、(式．３)を代入して、

　

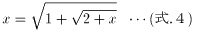
(式．４)に、(式．４)自身を代入して、

　

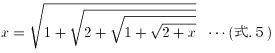
以下、同様に、(式．４)を代入し続けて、

　

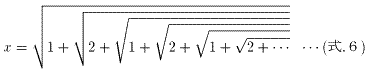
よって、求める極限値は、連立方程式(式．２、３)の解ｘである。
(式．２、３)より、

　

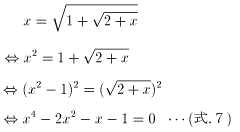
故に、(式．７)の四次方程式を解けばよいことになります。 そこで、フェラーリの公式を使って解いたのですが、得られた４個の解が、 全て還元不能のパターンになり、電卓で近似値を計算することができません。 そこで、(式．７)の四次方程式の解を求めるため、「ニュートン・ラフソン法」を使ってみました。

　

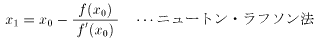
となり、ｘの近似値をして、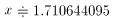が求まります。
これは、実際に、(式．１)を電卓で数十項まで計算した値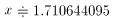（） と同じですから、(式．１)の近似値は求まったことになります。
しかし、真値がわかりません。(式．１)の連続根号数は、三角関数の値として表せることを確信しています。
というのは、実際に次のような例が知られているからです。

　

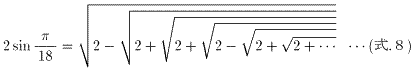
（(式．８)の極限値を求める問題は、八次方程式を解く問題に帰着されます。）
そこで、ｘ＝ｒ(cosθ＋ｉsinθ)とおいて、(式．７)の方程式を解こうとしたのですが、 計算が複雑になりすぎて手に負えなくなりました。以上、これまでの経過です。

NO.1791　　　　円錐台に内接する球(2)　　2009.6.15.　　夜ふかしのつらいおじさん

問１
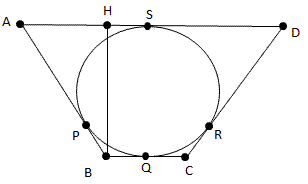
BからADに垂線を下ろす。
外部の点から円に引いた２本の接線において接点までの距離はそれぞれ等しい。
だから、AS＝AP、BQ＝BP
また、AH＝AS−BQ
△ABHに三平方の定理を用いると、

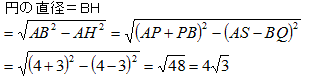
問２
問１において、AB＝ａ＋ｂ、ＡＨ＝ａ−ｂとすると、

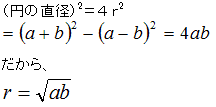
問３
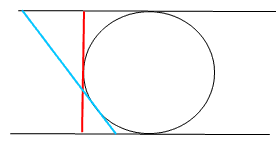
２本の平行線に円が接している。
この平行線にはさまれた円の接線は、平行線に垂直のときが一番短い。
このときの接線の長さは円の直径になる。（赤線）
問２より

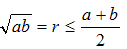
追加
この問題をみて思い出した例をかいておきます。
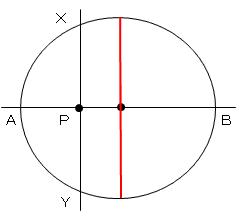
直径に垂直な縦線が交わっています。
方べきの定理より、
　　　ＰＡ・ＰＢ＝ＰＸ・ＰＹ
ここで、ＰＡ＝ａ、ＰＢ＝ｂとおきます。
ＰＸはＰが中心を通るとき最大になります。
すると、

NO.1790　　　　正三角形であることの証明　　2009.6.8.　　K.F.

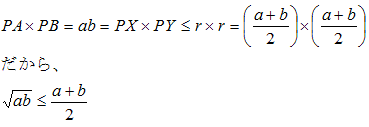
先日、見つけた大学時代のノートに、友人から出題された次のような問題 がありました。

問題：四辺形ＡＢＣＤが正方形のとき、三角形ＭＢＣが正三角形であることを 証明せよ。

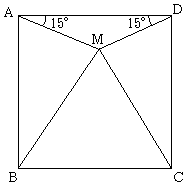
もちろん、高校生であれば、tan15°(=tan(45°-30°))を求めることにより簡単に解けます。
しかし、三角関数を使わなくても解くことができます。考えてみてください。

NO.1789　　　　円錐台に内接する球　　2009.6.1.　　水の流れ

第２２５回数学的な応募問題

先日、とあるバーへ飲みに行く機会があった。 同僚と同じ飲み物オン・ザ・ロックを注文したときのことである。 ロックグラスと丸氷の絶妙なセッテイングを目にした。 それは円錐台の形をしたグラスの高さが氷の直径に等しく、 しかもグラスの側面に氷が寄り添うようにぴったし収まっている光景だ。 どんなグラスと氷のときにこのような巧妙にマッチしたウイスキーを飲むことができるか暫し考えこんだ。 ここで、問題です。

問１．具体的な数値を知りたくて測ってみたところ、飲み口の面、つまり上底面の直径が８ｃｍ、 底にあたる面、下底面の直径が６ｃｍのグラスだと分かった。グラスの高さすなわち氷の直径を計算してください。

問２．次に、上底面の半径がa　ｃｍ、下底面の半径がｂ　ｃｍの円錐台に内接する球の半径　ｒをa、ｂで表せ。 参考に円錐台の底面の中心を通り、底面に垂直な平面によって切断した図を書いておく。

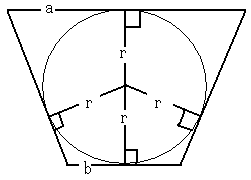
問３　問２の結果を用いて、正の数　a、ｂについての相加平均、相乗平均の大小関係を図から考察せよ。

注：この記事に関する投稿の掲載は、2009年６月15日以降とします。