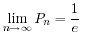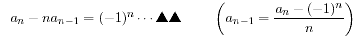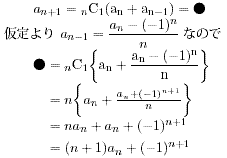NO.1619 約数の個数 2006.10.23. 水の流れ
第181回数学的な応募問題
皆さん、今年度の香川大学の入試問題を参考して出題します。是非チャレンジください。
数列{an}を次のように定める。
nの正の約数の個数が偶数ならば、an=0
nの正の約数の個数が奇数ならば、an=n
問題1:初項a1から第8項a8までの値を求めよ。
問題2:an=nとなるようなnはどのような数か理由をつけて答えよ。
問題3:初項a1から第2006項a2006までの和を求めよ。
問題4:初項a1から第n項anまでの和が2006以下となるようなnの最大整数を求めよ。
注:この記事に関する投稿の掲載は、11月13日以降とします。
NO.1618 第n次導関数(3) 2006.10.23. K.F.
対数関数の微分法と積の微分公式を用いると、f1(x)〜f7(x)について、
それぞれ下記の導関数が求まる。
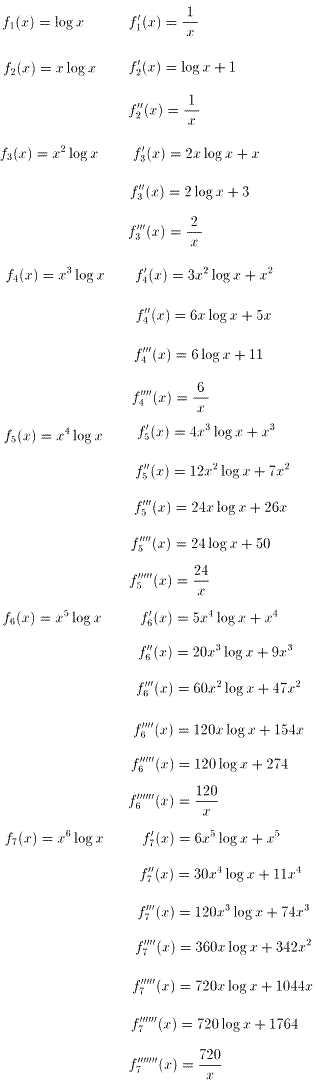
よって、問1の解は、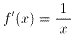 。
問2の解は、
。
問2の解は、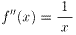 。
問3の解は、
。
問3の解は、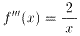 。
。
問4の解
fn(x)=g(n)/x とすると、下表のようになる。
| n | 1 | 2 | 3 | 4
| 5 | 6 | 7
|
|---|
| g(n) | 1 | 1 | 2 | 6
| 24 | 120 | 720
|
|---|
表から、g(n+1)/g(n)=n が成り立つように見えるから、g(n)=(n-1)! すなわち、
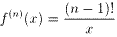
が類推できる。
問5の解(数学的帰納法による証明)
(i) n=1のとき、明らかに成り立つ。
(ii) n=kのとき、成り立つと仮定すると、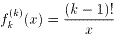 (式1)
(式1)
ところで、fk+1(x)=xklog x、fk(x)=xk-1log x なので、
fk+1(x)=xfk(x)となり、積xfk(x)にLeibnizの法則を用いて微分すると、
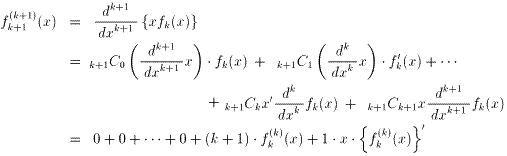 (式2)
(式2)
となる。式1、2より、
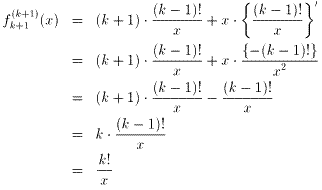
が成り立つ。故に、(i)、(ii)より、
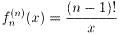
である。 (証明終わり)
NO.1617 第n次導関数(2) 2006.10.23. 蜘蛛の巣城
後の簡単のために、補助定理を示し証明しておきます。
補助定理:関数f、gがn階まで微分可能であるとき
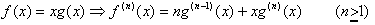
証明 積の微分法を利用して
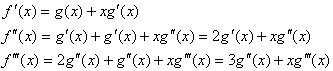
いずれも補助定理の形に収まります。
もし補助定理の形を仮定すれば微分して
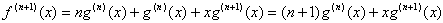
再び補助定理の形に収まります。 以上
本論です。
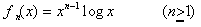
について
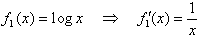
補助定理を使って次の事実を得ます。第1式右辺第2項は定数であることにご注意あれ。
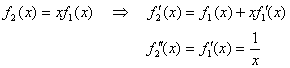
同様に
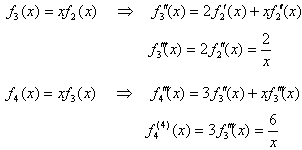
以上から次の形が推定されます。
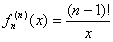 推定形
推定形
先ず、nの値1から4まで推定形に収まることは当然です、推定のもとですから。
また、推定形の成立を仮定して次の証明を得ます。
補助定理と仮定を使用して
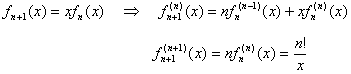
再び推定形に収まります。第1式右辺の第2項は仮定により定数です。
以上によって、推定形の成立が保証されました。
NO.1616 半整数四角形の問題 2006.10.1. 水の流れ
第180回数学的な応募問題
皆さん、「中尾さん」から頂いた問題にチャレンジください。
<中尾さんからのコメント:
最近、教えて!gooで、
「ラングレー問題(角度の問題の難問)を補助線なしで解きたい」
を見かけたので、類似の問題を考えてみました。
問題 半整角四角形の問題
四角形ABCDにおいて、∠ABD=(5/2)°,∠DBC=(125/2)°,∠ACB=(165/2)°,∠ACD=5°のとき、
∠ADBを求めよ。
注:この記事に関する投稿の掲載は、11月1日以降とします。
NO.1615 第n次導関数(1) 2006.10.1. 水の流れ
第179回数学的な応募問題
fn(x)=xn―1log x のとき、次の問に答えよ。
ただし、log x は自然対数とする。
問1:n=1のとき、第1次導関数 f'(x)を求めよ。
問2:n=2のとき、第2次導関数 f''(x)を求めよ。
問3:n=3のとき、第3次導関数 f'''(x)を求めよ。
問4:関数fn(x)の第n次導関数 f(n)(x)を類推して、nを用いて求めよ。
問5:関数fn(x)の第n次導関数 f(n)(x)の類推が正しいことを、数学的帰納法で証明せよ。
注:この記事に関する投稿の掲載は、10月23日以降とします。
NO.1614 完全順列(5) 2006.10.1. 蜘蛛の巣城
問1.
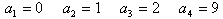
初項から第3項まではすぐわかります。第4項を導いた方法だけを書いておきます。
箱の番号は左から順につけます。数字は球の番号です。
図1は「3個の順列」をすべて示してあります。赤数字は箱と球の番号が一致しています。
図1
| (1)
| (2)
| (3)
|
| (1)
| (3)
| (2)
|
| (2)
| (1)
| (3)
|
| (2)
| (3)
| (1)
|
| (3)
| (1)
| (2)
|
| (3)
| (2)
| (1)
|
図2は図1のすべての順列に箱4を足して球(4)を入れてつくります。
「4個の順列」の一部です。当然すべての順列は「失格」です。
図2
(1)
| (2)
| (3)
| (4)
|
(1)
| (3)
| (2)
| (4)
|
(2)
| (1)
| (3)
| (4)
|
(2)
| (3)
| (1)
| (4)
|
(3)
| (1)
| (2)
| (4)
|
(3)
| (2)
| (1)
| (4)
|
図2の球(4)と球(1)を入れ替えて図3をつくります。
箱と球の番号が一致するもの同士を入れ替える点で、
1段2段は3段目以下と区別できます。
図3
(4)
| (2)
| (3)
| (1)
|
(4)
| (3)
| (2)
| (1)
|
(2)
| (4)
| (3)
| (1)
|
(2)
| (3)
| (4)
| (1)
|
(3)
| (4)
| (2)
| (1)
|
(3)
| (2)
| (4)
| (1)
|
図3で1段2段の合格数は、箱2箱3と球2球3でつくる「2個の順列」の合格数と同じです。
また、図1をみればわかるとおり3段目以下に「3個の順列」の合格の場合がすべて含まれていて、
且つ入れ替えの影響を受けませんから、3段目以下の合格数は「3個の順列」の合格数に等しいわけです。
ところで、「4個の順列」のすべては図2図3に加えて、
(4)と(2)また(4)と(3)の入れ替えをすれば得られますから次の式を得ます。
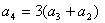
問2.
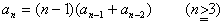
前問の解答文を一般化して書き表せばそのまま解答になります。略。
問3.前問の一般式を展開して
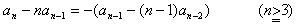
を得ます。公比 、初項 の等比数列の一般項は
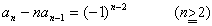
です。
問4.前問の結果を n! で割ると
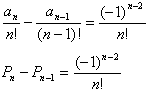
簡単のために
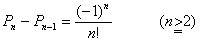
としていいでしょう。階差数列の和を利用して次の式を得ます。

ところで
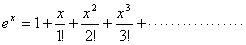
を借用すると
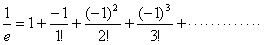
したがって

この事例からは「自然対数の底」がいかに自然な数であるかが感じられます。
彼の立場からみれば、整数などは醜悪な理解しがたい数に見えるのかも。
NO.1613 完全順列(4) 2006.10.1. 松井 満

NO.1612 完全順列(3) 2006.10.1. meira
題意の完全順列{an}の漸化式を求める。
1番目の箱にi(2≦i≦n)番目の球を入れて,j(2≦j≦n)番目の箱に1番目の球を入れる
とすると
i=jの場合,i番目の球と1番目の球を除く1からn-2までの完全順列でan-2通
り。……(1)
i≠jの場合,i番目の球を除く1からn-1までの完全順列でan-1通り。……(2)
(1),(2)の最初の球の選び方は1番目の球を除くn-1通りの選び方があるので,漸化式
anは
an=(n-1)(anー1+an-2)……(1)
問1
(1)のnに1から4まで当てはめると
問2
(1)
問3
(1)を変形して an-nanー1=(-1)(anー1-(n-1)an-2)
数列{an-nanー1}は初項{a2-21}=1,公比-1の等比数列であるので数列
{an-nanー1}は
an-nanー1=(-1)n-2=(-1)n……(2)
問4
1からnまでの並べ方はn!通りあるので,題意の確率Pnは
Pn=an/n!……(3)
(2)から数列{an}を求める。
(2)の両辺をn!で割ると
(an/n!)-(anー1/(n-1)!)=((-1)n)/n!
階差数列の求め方から
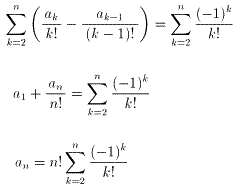
ここで,1!{((-1)0/0!)-(-1)(1)/1!}=1(1-1)=0を利用して
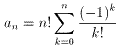 ・・・(4)
・・・(4)
これで数列{an}の一般項が求められた。
(4)を(3)に代入して
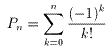
自然対数の底をeとして,exを級数展開して
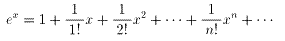
これにx=-1を代入し,nまで展開すると,
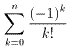 となる。
となる。
よってn→∞のとき,Pnの極限値は(1/e)。
NO.1611 完全順列(2) 2006.10.1. 夜ふかしのつらいおじさん
問1 a1=0、a2=1、a3=2、a4=9
問2 an=(n−1)(an−1+an−2)
問3 a
n−nan−1=(−1)n
問4 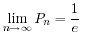
問1は具体的に調べます。a1=0は明らかです。
表1
| No | 1 2 | 1 2 3 | 1 2 3 4
|
|---|
| 1 | 2 1 | 2 3 1 | 2 1 4 3
| | 2 | | 3 1 2 | 2 4 1 3
| | 3 | | | 2 4 1 3
| | 4 | | | 3 1 4 2
| | 5 | | | 3 4 1 2
| | 6 | | | 3 4 2 1
| | 7 | | | 4 1 2 3
| | 8 | | | 4 3 1 2
| | 9 | | | 4 3 2 1
|
さて、この球の入れ方を次ぎのように表すことにします。
a4の場合を例にします。
表2
| No | 1 2 3 4 | 表現
|
|---|
| 1 | 2 1 4 3 | (12)(34)
| | 2 | 2 4 1 3 | (1234)
| | 3 | 2 4 1 3 | (1243)
| | 4 | 3 1 4 2 | (1342)
| | 5 | 3 4 1 2 | (13)(24)
| | 6 | 3 4 2 1 | (1324)
| | 7 | 4 1 2 3 | (1432)
| | 8 | 4 3 1 2 | (1423)
| | 9 | 4 3 2 1 | (14)(23)
|
(12)と(21)とは、同じものですが、括弧( )の中は最小の数を先頭に書くことにします。
a4の場合は、(oooo)、(oo)(oo)(注:ooは何か数字)の2つのパターンがあり、
括弧( )の中で閉じています。
a3の場合は、(ooo)の1つのパターンしかありません。
さて、問2は次のように考えます。a3からa4に拡大する場合で
説明します。a3の場合球の入れ方は次の2通りです。
(123),(132)
これをもとに{4}をつけたすことを考えます。
次のaからcの場合があり順に表2のNo:8,3,2(左のとき),7,4,6(右のとき)になります。
(a3 × 3C1 ・・・★)
(1a2b3c), (1a3b2c)
しかし、この方法ではつけたす{4}と他の数の2つで閉じる(2)のパターンが出てきません。
そこで、4と組み合わせる数を{1,2,3}から選び残る2つの並べ方を考えます。
(3C1 × a2・・・ ★★)
この2つの場合(★と★★)を合計すれば良いので、一般的に表現すれば、
an=n−1C1(an−1+an−2) ・・・ ▲
問3は難しいので具体的にやってみます。
まず、nが偶数のときは、
n=2のとき、a2−2a1=1−2×0=1
n=4のとき、a4−4a3=9−4×2=1
次に、nが奇数のときは、
n=3のとき、a3−3a2=2−3×1=−1
まとめて、
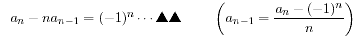
となりそうです。良い説明を思いつかないのでこじつけます。
nが小さいときは具体的に調べて確認できているので、
n以下のときに▲▲の式が成立すると仮定します。
▲の式は正しいものとしてとしてn+1のときは、
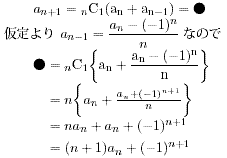
問4は強引にやってみます。

|
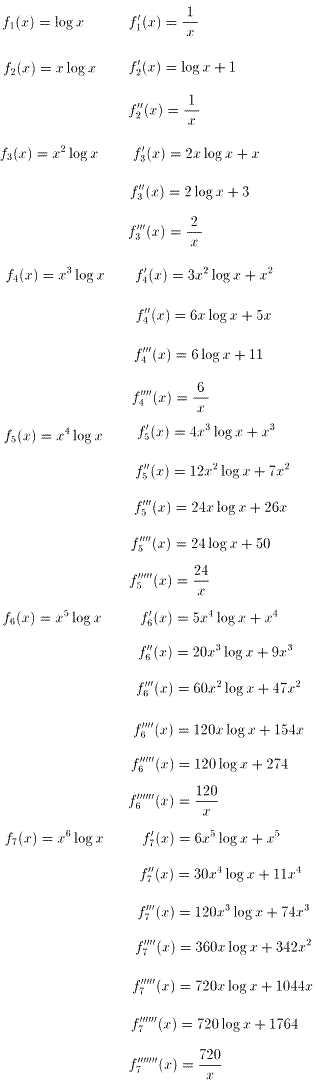
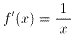 。
問2の解は、
。
問2の解は、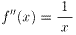 。
問3の解は、
。
問3の解は、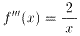 。
。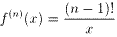 が類推できる。
が類推できる。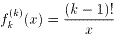 (式1)
(式1)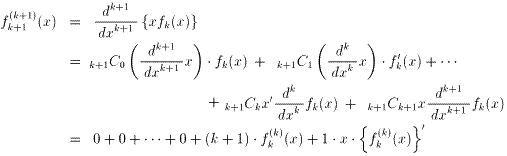 (式2)
(式2)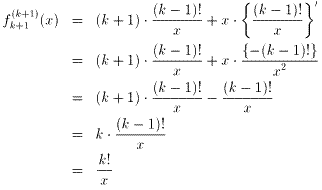
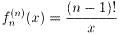
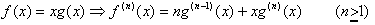
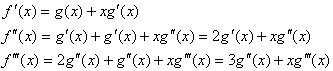
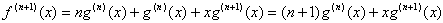
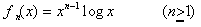
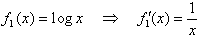
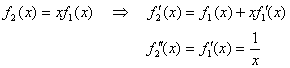
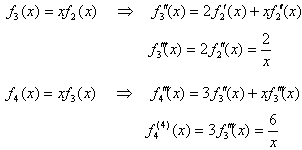
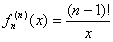 推定形
推定形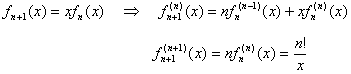
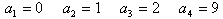
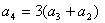
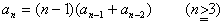
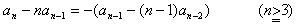
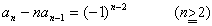
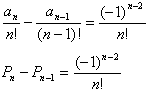
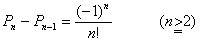

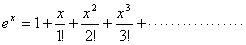
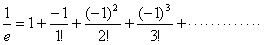


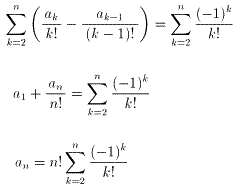
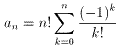 ・・・(4)
・・・(4)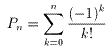
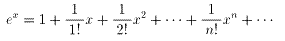
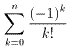 となる。
となる。