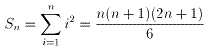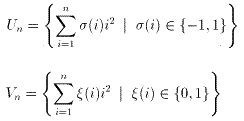Colloquium

NO.207
Weekend Mathematics／コロキウム室／NO.207

NO.1603　　特製正ｎ面体サイコロ　　2006.7.9.　　水の流れ

第１７５回数学的な応募問題

皆さん、一般に普通のサイコロは正６面体で、目は自然数の１から６が書いてあります。 ここで、２個のサイコロを投げたとき、目の和の出方が普通のサイコロと同じようであるような特製のサイコロを考えます。 だから、２つのサイコロは同一ある必要はないですし、その目が６以下である必要もない。また、すべて異なる目である必要もありません。 このような問題をNO.548　特製のサイコロ(1)として出題しました。 これの拡張問題です。

問１：正４面体のサイコロを２個投げたとき、目の和の出方が普通のサイコロと同じようであるような特製のサイコロの目を考えてください。

問２：正八面体のサイコロを２個投げたとき、目の和の出方が普通のサイコロと同じようであるような特製のサイコロの目を考えてください。

問３：正十二面体のサイコロを２個投げたとき、目の和の出方が普通のサイコロと同じようであるような特製のサイコロの目を考えてください。

問４：正二十面体のサイコロを２個投げたとき、目の和の出方が普通のサイコロと同じようであるような特製のサイコロの目を考えてください。

＜コメント：問１は１組、問２は３組、問３は未解決、問４は未解決です。教えてくだされば幸いです。＞

注：この記事に関する投稿の掲載は、７月３１日以降とします。

NO.1602　　平方数の和と差(7) 　　2006.7.8.　　まこぴ〜

副題：Ｖｎの決定からＵｎの決定

Ｎを自然集の集合、Ｚを整数の集合とします。
前稿に引き続き

　　　

　　　

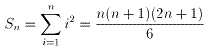
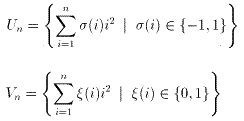
　　　ａ，ｂ∈Ｚのとき　　［ａ，ｂ］Ｚ＝｛ｘ｜ｘ∈Ｚ、ａ≦ｘ≦ｂ｝

　　　Ｖ’ｎ＝［０，Ｓｎ］Ｚ−Ｖｎ

とします。

加法「＋」、乗法「・」が定義できる集合Ａがあり、ｂ∈Ａ、Ｂ⊂Ａにたいして、

　　　Ｂ＋ｂ＝｛ｘ＋ｂ｜ｘ∈Ｂ｝
　　　Ｂ−ｂ＝｛ｘ−ｂ｜ｘ∈Ｂ｝
　　　ｂＢ＝｛ｂ・ｘ｜ｘ∈Ｂ｝

とおきます。特に−Ｂ＝（−１）Ｂとします。
前稿で示した予想「ｎ≧９であれば、どうやら＃Ｖ’ｎ＝ 62 となる「らしい」。」を考えてみたい。

Ｖ’ｎを計算する様子をエラトステネスの篩の要領で示してみます。
まず、数表を用意します。
0123456789
10111213141516171819
20212223242526272829


Ｖ１を消します。
0123456789
10111213141516171819
20212223242526272829


Ｖ２を消します。
0123456789
10111213141516171819
20212223242526272829


Ｖ３を消します。
0123456789
10111213141516171819
20212223242526272829


Ｖ４を消します。Ｓ４＝３０ですので、表を３０まで追加しましょう。
0123456789
10111213141516171819
20212223242526272829
30


Ｖ５を消します。Ｓ５＝５５ですので、表を５５まで追加しましょう。
0123456789
10111213141516171819
20212223242526272829
30313233343536373839
40414243444546474849
505152535455


この要領で続けていき、Ｖ１１まで消すと、次のようになります（Ｓ１１＝５０６）。
0123456789
10111213141516171819
20212223242526272829
30313233343536373839
40414243444546474849
50515253545556575859
60616263646566676869
70717273747576777879
80818283848586878889
90919293949596979899
100101102103104105106107108109
110111112113114115116117118119
120121122123124125126127128129
130131132133134135136137138139
140141142143144145146147148149
中略
350351352353354355356357358359
360361362363364365366367368369
370371372373374375376377378379
380381382383384385386387388389
390391392393394395396397398399
400401402403404405406407408409
410411412413414415416417418419
420421422423424425426427428429
430431432433434435436437438439
440441442443444445446447448449
450451452453454455456457458459
460461462463464465466467468469
470471472473474475476477478479
480481482483484485486487488489
490491492493494495496497498499
500501502503504505506


「中略」の部分はすべて消える部分です。

途中を省略しましたが、前述の

　　Ｐ∈Ｖ’ｎ　ならば　　Ｓｎ−Ｐ∈Ｖ’ｎ

をｎ≦１１の場合に確認できると思います。
また、ｎ＝１１の表から前半部分を抜き出すと、

　　Ｘ＝｛2, 3, 6, 7, 8, 11, 12, 15, 18, 19, 22, 23, 24, 27, 28, 31, 32, 33, 43, 44, 47, 48, 60, 67, 72, 76, 92, 96, 108, 112, 128｝

となります。

そこで、表の中で横線を引いた部分がＶｎの元であることに注意すると

　　５．　ｎ≧９のとき、［１２９，Ｓｎ−１２９］Ｚ⊂Ｖｎ

（証明）
（１）　９≦ｎ≦１０のときは、上の数表から直接従う。
（２）　ｎ≧１１のとき、

　　［１２９，Ｓｎ−１−１２９］Ｚ⊂Ｖｎ−１

と仮定します。Ｖｎ＝Ｖｎ−１∪（Ｖｎ−１＋ｎ２）であるので、

　　［１２９，Ｓｎ−１−１２９］Ｚ∪［１２９＋ｎ２，Ｓｎ−１２９］Ｚ⊂Ｖｎ

となるが、

　　　６（（Ｓｎ−１−１２９）−（１２９＋ｎ２））
　　＝（２ｎ３−９ｎ２＋ｎ−１５８４）＋３６
　　＝（ｎ−１１）（２ｎ２＋１３ｎ＋１４４）＋３６
で、最後の式の２次式の判別式が負であることを考慮すると、ｎ≧１１ならば

　　１２９＜１２９＋ｎ２＜Ｓｎ−１−１２９＜Ｓｎ−１２９

であることから、

　　　［１２９，Ｓｎ−１２９］Ｚ＝［１２９，Ｓｎ−１−１２９］Ｚ∪［１２９＋ｎ２，Ｓｎ−１２９］Ｚ⊂Ｖｎ

よって、数学的帰納法により、主張が正しいことが示された。（証明終わり）

次にＸとＶ’ｎの包含関係について、次が成り立ちます。

　　６．　ｎ≧７　ならば　Ｘ⊂Ｖ’ｎ

（証明）
（１）　７≦ｎ≦１１のときは、上の数表から直接従う。
（２）　ｎ≧１２のとき、

　　Ｖｎ＝Ｖｎ−１∪（Ｖｎ−１＋ｎ２）

で、ｘ∈Ｖｎ−Ｖｎ−１とすると、ｘ≧ｎ２≧１４４＞１２８なので
Ｖｎ−Ｖｎ−１の元は１２８より大である。（証明終わり）

以上のことから、Ｖ’ｎ、Ｖｎ、Ｕｎを次のように決定できる。

　　７．　すべてのｎ∈Ｎについて、

　　　　Ｖ’ｎ＝［０，Ｓｎ］Ｚ∩（Ｘ∪（−Ｘ＋Ｓｎ））

　　　　Ｖｎ＝［０，Ｓｎ］Ｚ−（Ｘ∪（−Ｘ＋Ｓｎ））

　　　　Ｕｎ＝２Ｖｎ−Ｓｎ

　　　　　　＝（２［０，Ｓｎ］Ｚ−Ｓｎ）−（２Ｘ−Ｓｎ）∪（−（２Ｘ−Ｓｎ））

　　　となる。

これをもとにｎ＝４のときを計算してみる。
　　　Ｓ４＝３０
　　　［０，Ｓ４］Ｚ＝｛0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30｝
　　　Ｘ＝｛2,3,6,7,8,11,12,15,18,19,22,23,24,27,28,31,32,33,43,44,47,48,60,67,72,76,92,96,108,112,128｝
　　　２Ｘ−Ｓ４＝｛-26,-24,-18,-16,-14,-8,-6,0,6,8,14,16,18,24,26,32,34,36,56,58,64,66,90,104,114,122,154,162,186,194,226｝
　　　Ｖ’４＝［０，Ｓ４］Ｚ∩（Ｘ∪（−Ｘ＋Ｓ４）
　　　　　　＝｛2,3,6,7,8,11,12,15,18,19,22,23,24,27,28｝
　　　Ｖ４＝［０，Ｓｎ］Ｚ−（Ｘ∪（−Ｘ＋Ｓｎ））
　　　　　＝｛0,1,4,5,9,10,13,14,16,17,20,21,25,26,29,30｝
　　　Ｕ４＝｛-30,-28,-22,-20,-12,-10,-4,-2,2,4,10,12,20,22,28,30｝

注目すべきは、ＳｎとＸですべての計算ができることである。

戻る