| NO.1550 | 2005.8.16. | 佐野允信 | 不思議な平方根(2) |
問1
a2-a=a(a-1)
と表せる。aは奇数だから、a-1は偶数である。
10000=104=24×54
と表せ、a2-aが、10000で割り切れるから、
a-1=24k=16k(kは整数) ・・・(1)
でなければならない。
a-1=24×54
とすると、
a>10001>9999
となり条件に反するから、
a=5l(lは整数) ・・・(2)
でなければならない。(1),(2)より、
16k+1=5l
∴ 5l-16k=1 ・・・(3)
5×(-3)-16×(-1)-1より、
5(l+3)-16(k+1) ・・・(4)
5と16は互いに素だから、
l+3=16p (pは整数)
k+1=5p
でなければならない。
∴ l=16p-3 ・・・(5)
k=5p-1 ・・・(6)
(6)を(1)に代入すると、
a-1=16(5p-1) ・・・(8)
となるので、a-1は、5の倍数ではない。したがって、
a=54m=625m=(mは整数) ・・・(9)
でなければならない。(8)、(9)より、
80p-15=625m
∴ 16p-125m=3 ・・・(10)
16×8-125×1=3より、
16(p-8)-125(m-1)=0
∴ 16(p-8)=125(m-1)
16と125は互いに素だから
p-8-125q(qは整数)
m-1-16q
でなければならない。
∴ p=125q+8 ・・・(12)
m=16q+1 ・・・(13)
条件より、
3≦a≦9999
だから、(9)より、
3≦625m≦9999
∴ 1≦m≦15 ・・・(14)
(13)を(14)に代入すると
1≦16q+1≦15
∴ q=0 ・・・(15)
(15)を(13)に代入すると
m=1 ・・・(16)
(16)を(9)に代入すると、
a=625 ・・・(17)
このとき、
a2-a=a(a-1)=625×624=390000
となり、10000で割り切れる。従って、求める数は、
a=625 ・・・(答)
問2
√Nは、1ケタの整数より、
0≦√N≦9 ・・・(1)
∴ 0≦N≦81 ・・・(2)
したがって、
N=10a1+a0
(0≦a0,1≦9;a0,1は整数) ・・・(3)
と表せる。条件より
10a1+a0=a02
∴ a0(a0-1)=10a1 ・・・(4)
(Ⅰ)a0≠0,1のとき
(4)より、a0(a0-1)は10で割り切れなければならない。
(i)a0が奇数のとき
a0-1は、偶数だから
a0-1=2k(kは整数) ・・・(5)
でなければならない。
a0-1=2×5
とすると
a0=11>9
となり、(1)に反するから
a0=5l(lは整数) ・・・(6)
でなければならない。(1)、(5)、(6)より
a0=5 ・・・(7)
このとき、
a0(a0-1)=5×4=20 ・・・(8)
となり、10で割り切れる。(4)、(8)より、
a1=2 ・・・(9)
(7)、(9)より、
N=25 ・・・(10)
これは与えられた条件を満たす。
(ii)a0が偶数のとき
a0-1は、奇数だから
a0=2k'(k'は整数) ・・・(11)
でなければならない。
a0=2×5=10
とすると、(1)に反するから
a0-1=5l'(l'は整数) ・・・(12)
でなければならない。(1)、(11)、(12)より
a0=6 ・・・(13)
このとき、
a0(a0-1)=6×5=30 ・・・(14)
となり、10で割り切れる。(4)、(14)より、
a1=3 ・・・(15)
(13)、(15)より、
N=36 ・・・(17)
これは与えられた条件を満たす。
(Ⅱ)a0=0のとき
(4)より、a1=0 ・・・(18)
よって、N=0 ・・・(19)
BR> これは与えられた条件を満たす。
(Ⅲ)a0=1のとき
(4)より、a1=0 ・・・(20)以上、(Ⅰ)、(Ⅱ)、(Ⅲ)より、求める数は、
よって、N=1 ・・・(21)
BR> これは与えられた条件を満たす。
N=0,1,25,36 ・・・(答)
つづく

| NO.1551 | 2005.8.16. | 水の流れ | 綺麗な不等式 |
皆さん、今回の問題です。考えてください。

注)この記事に関する投稿の掲載は、9月5日以降とします。

| NO.1552 | 2005.8.21. | 佐野允信 | 不思議な平方根(3) |
NO.1550のつづきです。
問3
√Nは、2ケタの整数より、
10≦√N≦99 ・・・(1)
∴ 100≦N≦9801 ・・・(2)
したがって、
N=103a3+102a2+10a1+a0
(0≦a0,a1,a2,a3≦9
;a0,a1,a2,a3は整数) ・・・(3)
と表せる。条件より
103a3+102a2+10a1+a0=(10a1+a0)2
∴ (10a1+a0){(10a1+a0)-1}=102(10a3+a2) ・・・(4)
ここで、
α=10a1+a0 ・・・(5)
とおくと、(4)より、α(α-1)は、102でわりきれなければならない。
(i)αが奇数のとき
α-1は、偶数だから
α-1=22k=4k(kは整数) ・・・(6)
でなければならない。
α-1=22×52
とすると
α=101>99
となり、(1)に反するから
α=5l(lは整数) ・・・(7)
でなければならない。(6)、(7)より
4k+1=5l
このとき、
∴ 5l-4k=1 ・・・(8)
5×1-4×1=1より
5(l-1)-4(k-1)=0
∴ 5(l-1)=4(k-1)
4と5は互いに素だから、
l-1=4p (pは整数)
k-1=5p
でなければならない。
∴ l=4p+1 ・・・(9)
k=5p+1 ・・・(10)
(6)を(10)に代入すると、
-1=4(5p+1) ・・・(11)
となるので、α-1は、5の倍数ではない。したがって、
a=52m=25m=(mは整数) ・・・(12)
でなければならない。(11)、(12)より
20p+5=25m
∴ 5m-4p=1 ・・・(13)
5×1-4×1=1より
5(m-1)-4(p-1)=0
∴ 5(m-1)=4(p-1) ・・・(14)
4と5は互いに素だから、
m-1=4q (qは整数)
p-1=5q
でなければならない。
∴ m=4q+1 ・・・(15)
p=5q+1 ・・・(16)
(12)を(1)に代入すると、
10≦25m≦99
∴ 1≦m≦3 ・・・(17)
(15)を(17)に代入すると
1≦4q+1≦3
∴ q=0 ・・・(18)
(12),(15),(18)より、
α=25
このとき、α(αー1)=25×24=6×102
となり、102で割り切れる。
(4),(5),(19)より、
10a3+a2=6 ・・・(20)
(19),(20)より
N=625 ・・・(21)
これは与えられた条件を満たす。
(ii)αが偶数のとき
α-1は、奇数だから
α=22k'=4k'(k'は整数) ・・・(22)
でなければならない。
α=22×52=100
とすると(1)に反するから
αー1=5l'(l'は整数) ・・・(23)
でなければならない。(22)、(23)より
5l'+1=4k'
∴ 4k'ー5l'=1 ・・・(24)
4×(-1)-5×(-1)=1より
4(k'+1)-5(l'+1)=0
∴ 4(k'+1)=5(l'+1)
4と5は互いに素だから、
l'+1=4p' (p'は整数)
k'+1=5p'
でなければならない。
∴ l'=4p'-1 ・・・(25)
k'=5p'-1 ・・・(26)
(22)を(26)に代入すると、
α=4(5p'-1) ・・・(27)
となるので、αは、5の倍数ではない。したがって、
a-1=52m'=25m'=(m'は整数) ・・・(28)
でなければならない。(27)、(28)より
20p'-4=25m'+1
∴ 4p'-5m'=1 ・・・(29)
4×(-1)-5×(-1)=1より
4(p'+1)-5(m'+1)=0
∴ 4(p'+1)=5(m'+1)
4と5は互いに素だから、
p'+1=5q' (q'は整数)
m'+1=4q'
でなければならない。
∴ p'=5q'-1 ・・・(30)
m'=4q'-1 ・・・(31)
(28)を(1)に代入すると、
10≦25m'+1≦99
∴ 1≦m'≦3 ・・・(32)
(31)を(32)に代入すると
1≦4q'-1≦3
∴ q'=1 ・・・(33)
(28),(31),(33)より、
α=76
このとき、α(αー1)=76×75=57×102
となり、102で割り切れる。
(4),(5),(34)より、
10a3+a2=57 ・・・(35)
(34),(35)より
N=5776 ・・・(36)
これは与えられた条件を満たす。
以上、(i)(ii)より、求める数は、
N=625,5776 ・・・(答)
問4
√Nは、3ケタの整数より、
100≦√N≦999 ・・・(1)
∴ 10000≦N≦998001 ・・・(2)
したがって、
N=105a5+104a4+
103a3+102a2+10a1+a0
(0≦a0,a1,・・・,a5≦9
;a0,a1,・・・,a5は整数) ・・・(3)
と表せる。条件より
105a5+104a4+
103a3+102a2+
10a1+a0=(102a2+10a1+a0)2
∴ (102a2+10a1+a0)
{(102a2+10a1+a0)-1}
=103(102a5+10a4+a3) ・・・(4)
ここで、
α=102a2+10a1+a0 ・・・(5)
とおくと、(4)より、α(α-1)は、103でわりきれなければならない。
(i)αが奇数のとき
α-1は、偶数だから
α-1=23k=8k(kは整数) ・・・(6)
でなければならない。
α-1=23×53
とすると
α=1001>999
となり、(1)に反するから
α=5l(lは整数) ・・・(7)
でなければならない。(6)、(7)より
8k+1=5l
このとき、
∴ 5l-8k=1 ・・・(8)
5×(-3)-8×(-2)=1より
5(l+3)-8(k+2)=0
∴ 5(l+3)=8(k+2)
5と8は互いに素だから、
l+3=8p (pは整数)
k+2=5p
でなければならない。
∴ l=8p-3 ・・・(9)
k=5p-2 ・・・(10)
(6)を(10)に代入すると、
α-1=8(5p-2) ・・・(11)
となるので、α-1は、5の倍数ではない。したがって、
a=53m=125m=(mは整数) ・・・(12)
でなければならない。(11)、(12)より
40p-15=125m
∴ 8p-25m=3 ・・・(13)
8×(-9)-25×(-3)=3より
8(p+9)-25(m+3)=0
∴ 8(p+9)=25(m+3) ・・・(14)
8と25は互いに素だから、
m+3=8q (qは整数)
p+9=25q
でなければならない。
∴ m=8q-3 ・・・(15)
p=25q-9 ・・・(16)
(12)を(1)に代入すると、
100≦125m≦999
∴ 1≦m≦7 ・・・(17)
(15)を(17)に代入すると
1≦8q-3≦7
∴ q=1 ・・・(18)
(12),(15),(18)より、
α=625 ・・・(19)
このとき、α(αー1)=625×624=390×103
となり、103で割り切れる。
(4),(5),(19)より、
102a5+10a4+a3=390
∴ a5=3,a4=9,3=0 ・・・(20)
(19),(20)より
N=390625 ・・・(21)
これは与えられた条件を満たす。
(ii)αが偶数のとき
α-1は、奇数だから
α=23k'=8k'(k'は整数) ・・・(22)
でなければならない。
α=23×53=1000
とすると(1)に反するから
αー1=5l'(l'は整数) ・・・(23)
でなければならない。(22)、(23)より
5l'+1=8k'
∴ 8k'-5l'=1 ・・・(24)
8×2-5×3=1より
8(k'-2)-5(l'-3)=0
∴ 8(k'-2)5(l'-3)
5と8は互いに素だから、
l'-3=8p' (p'は整数)
k'-2=5p'
でなければならない。
∴ l'=8p'+3 ・・・(25)
k'=5p'+2 ・・・(26)
(22)を(26)に代入すると、
α=8(5p'+2) ・・・(27)
となるので、αは、5の倍数ではない。したがって、
a-1=53m'=125m'=(m'は整数) ・・・(28)
でなければならない。(27)、(28)より
40p'+16=125m'+1
∴ 25m'-8p'=3 ・・・(29)
25×3-8×9=3より
25(m'-3)-8(p'-9)=0
∴ 25(m'-3)=8(p'-9)
8と25は互いに素だから、
p'-9=25q' (q'は整数)
m'-3=8q'
でなければならない。
∴ p'=25q'+9 ・・・(30)
m'=8q'+3 ・・・(31)
(28)を(1)に代入すると、
100≦125m'+1≦999
∴ 1≦m'≦7 ・・・(32)
(31)を(32)に代入すると
1≦8q'+3≦7
∴ q'=0 ・・・(33)
(28),(31),(33)より、
α=376 ・・・(34)
このとき、α(αー1)=376×375=141×103
となり、103で割り切れる。
(4),(5),(34)より、
102a5+10a4+a3=141
∴ a5=1,a4=4,3=1 ・・・(35)
(34),(35)より
N=141376 ・・・(36)
これは与えられた条件を満たす。
以上、(i)(ii)より、求める数は、
N=141376,390625 ・・・(答)
問5
√Nは、4ケタの整数より、
1000≦√N≦9999 ・・・(1)
∴ 1000000≦N≦99980001 ・・・(2)
したがって、
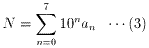
(0≦a0,a1,・・・,a7≦9
;a0,a1,・・・,a7は整数)
と表せる。条件より
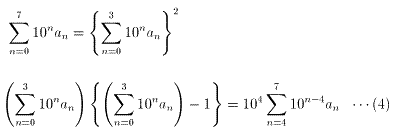
ここで、
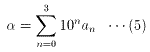
とおくと、(4)より、α(α-1)は、104でわりきれなければならない。
(i)αが奇数のとき
α-1は、偶数だから
α-1=24k=16k(kは整数) ・・・(6)
でなければならない。
α-1=24×54
とすると
α=10001>9999
となり、(1)に反するから
α=5l(lは整数) ・・・(7)
でなければならない。(6)、(7)より
16k+1=5l
このとき、
∴ 5l-16k=1 ・・・(8)
5×(-3)-16×(-1)=1より
5(l+3)-16(k+1)=0
∴ 5(l+3)=16(k+1)
5と16は互いに素だから、
l+3=16p (pは整数)
k+1=5p
でなければならない。
∴ l=16p-3 ・・・(9)
k=5p-1 ・・・(10)
(6)を(10)に代入すると、
α-1=16(5p-1) ・・・(11)
となるので、α-1は、5の倍数ではない。したがって、
a=54m=625m=(mは整数) ・・・(12)
でなければならない。(11)、(12)より
80p-15=625m
∴ 16p-125m=3 ・・・(13)
18×8-125×(-1)=3より
16(p-8)-125(m-1)=0
∴ 16(p-8)=125(m-1) ・・・(14)
16と125は互いに素だから、
m-1=16q (qは整数)
p-8=125q
でなければならない。
∴ m=16q+1 ・・・(15)
p=125q+8 ・・・(16)
(12)を(1)に代入すると、
1000≦625m≦9999
∴ 2≦m≦15 ・・・(17)
(15)を(17)に代入すると
2≦16q+1≦15
よってこれを満たすqは存在しない。したがって、αが奇数のとき、与えられた条件を満たすNは存在しない。
(ii)αが偶数のとき
α-1は、奇数だから
α=24k'=16k'(k'は整数) ・・・(18)
でなければならない。
α=24×54=10000
とすると(1)に反するから
αー1=5l'(l'は整数) ・・・(19)
でなければならない。(18)、(19)より
5l'+1=16k'
∴ 168k'ー5l'=1 ・・・(20)
16×1-5×3=1より
16(k'-1)-5(l'-3)=0
∴ 16(k'-1)=5(l'-3)
5と16は互いに素だから、
l'-3=16p' (p'は整数)
k'-1=5p'
でなければならない。
∴ l'=16p'+3 ・・・(21)
k'=5p'+1 ・・・(22)
(18)を(22)に代入すると、
α=16(5p'+1) ・・・(23)
となるので、αは、5の倍数ではない。したがって、
a-1=54m'=625m'=(m'は整数) ・・・(24)
でなければならない。(23)、(24)より
80p'+16=625m'+1
∴ 125m'-16p'=3 ・・・(25)
125×(-1)-16×(-8)=3より
125(m'+1)-16(p'+8)=0
∴ 125(m'+1)=16(p'+8)
16と125は互いに素だから、
p'+8=125q' (q'は整数)
m'+1=16q'
でなければならない。
∴ p'=125q'-8 ・・・(26)
m'=16q'-1 ・・・(27)
(24)を(1)に代入すると、
1000≦625m'+1≦9999
∴ 2≦m'≦15 ・・・(28)
(27)を(28)に代入すると
2≦16q'-1≦15
∴ q'=1 ・・・(29)
(24),(27),(29)より、
α=9376 ・・・(30)
このとき、α(αー1)=9376×9375=8790×104
となり、104で割り切れる。
(4),(5),(30)より、
103a7+102a6+10a5+a4=8790
∴ a7=8,a6=7,5=9,4=0 ・・・(31)
(30),(31)より
N=87909376 ・・・(32)
これは与えられた条件を満たす。
以上、(i)(ii)より、求める数は、
N=87909376 ・・・(答)

 E-mail
E-mail
 戻る
戻る