| NO.1506 | 2005.1.1. | Junko | 2005年あけましておめでとうございます。 |
2005年、あけましておめでとうございます。
元旦を迎えて、今年はどんな年になるのだろうかと思いめぐらせています。
私自身は、自分に与えられた場面場面において一生懸命やっていきたいと思っています。
皆さんにとっても、よい年になるよう、お祈りしています。

| NO.1507 | 2005.1.1. | DDT | 超ハード数学SF?(2) |
NO.1491の図-2について、小島先生から「疑問(「隣り合った有理点」という表現がしっくりきません。なぜならご承知の通り、2つの有理点の間には、これまた無数の有理点が存在するからです。)」が届いておりました。
今さらながらですが、私なりの返答をいたしたいと思います。
1.隣り合った有理数の間で、連続関数は不連続になることはない
まず「隣り合った有理数」という表現を許してください。これに対する私なりの解答は、次に示します。
隣り合った有理数の間で、連続関数は不連続になることはない.
これこそが「等式延長の原理」が述べていることです。ただし、実際に行える数値計算では有理数上でのシミュレーションが精一杯で、隣り合った有理数の間で解関数が連続であることは、実際には数値計算で確認できません。 それを言うためには、どうしても「等式延長の原理」が必要だということをはっきりと言いたいがために、図-2には不連続な場合も含めました。例えば次のような例があります。
連続関数のフーリエ変換には、不連続な原関数も含めると無数の逆変換が対応し、その不連続関数の同値類に対して逆変換の一意性が成り立つ。もちろん不連続関数の同値類の積分平均は、もとの連続関数である。
2.隣り合った有理数
これは参りました。もともと有理数と自然数が同数であることを言いたいがために、可算無限倍率の顕微鏡を持ち出しました。これがあれば稠密な有理数を、自然数直線上に離散化できると思ったからです。
しかし隣り合った有理数という表現そのものに無理がありました。隣り合った有理数には、1/∞の差しかありません。NO.1485で自分自身で証明してみせたように(ちょっといい加減でしたが)、分母が∞になる有理数とは無理数のことです。小島先生が仰る様に、隣り合った有理数というものは、もともと我々には観測不可能で、図-2は、可算無限倍率顕微鏡の可算極限操作の途中の図でなければなりません。本当に、
無限とは有限ではないこと.
なのだと、あらためて思いました。では、
これは悲しすぎます.
そして有理数と自然数は同数なのです。
隣り合った有理数という考えは、あって欲しい・・・。
もちろん「位相と基数は別物だ!」と言われれば、その通りです。
だから次のような解釈はどうでしょう?。
NO.1491の図-2は、NO.1485で捏造した「可算無限寿命人」が見た有理数の姿だったのです。この人にとって、可算無限は有限なので、隣り合った有理数はNO.1491の図-2のように見えるのです。結局、可算無限倍率顕微鏡とは、有限人(我々)に可算無限人の視点を与えてくれる変換装置だったという解釈です。そもそも可算無限倍率顕微鏡は、こういうことを自由自在にやれたらいいな、と思って導入したものでした。関数の一点の中には、1次関数が住んでいると思いたいからです。だけど、やりすぎですね。

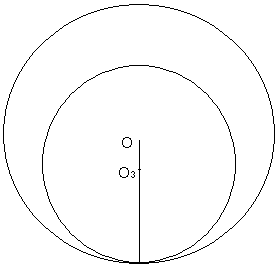
| NO.1508 | 2005.1.3. | 水の流れ | 外接する3円 |
最近、中央新書から出版された秋山仁著の「知性の織りなす数学美」という本を読んでいます。その中に、
江戸時代の和算家『関孝和』のこぼれ話が出ていました。次の問題が出ていて、生徒と一緒に解き始めましたが、
未だに解けていません。では、その問題です。
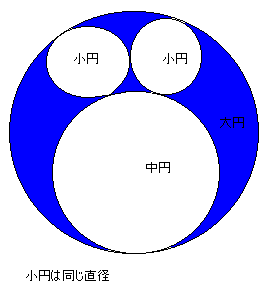
図の青の部分の面積が120、中円と小円の直径の差が5であるとき、大、中、小の3種類の直径を求めよ。
だだし、中円と小円は互いに外接、中円と大円は内接、2つの小円と大円は内接している。
【追記】
実は、問題文は「知性の織りなす数学美」にある通りですが、生徒と考えていたとき気がついたのですが、
図の青の部分の面積が120は誤記のような気がします。
そこで、面積を120π(πは円周率)としても考えてください。
さらに、類題として、図の通りの4つの円で、大円、中円、小円の半径をそれぞれ、R,r ,t としたとき、tをR,rで表してください。(この類題が和算の本にあるものです)

| NO.1509 | 2005.1.15. | Mit | 2005作り (2) |
問題3~5までJavaプログラムで解きました。 結果は以下のとおりです。
問題3
196 ... 205
399 ... 403
1002 ... 1003
問題4
f(x) = x(x+1)/2
(f(1), f(26), f(57)) = (1, 351, 1653)
(f(2), f(28), f(56)) = (3, 406, 1596)
(f(6), f(42), f(46)) = (21, 903, 1081)
(f(8), f(12), f(61)) = (36, 78, 1891)
(f(9), f(19), f(59)) = (45, 190, 1770)
(f(10), f(15), f(60)) = (55, 120, 1830)
(f(10), f(30), f(54)) = (55, 465, 1485)
(f(11), f(33), f(52)) = (66, 561, 1378)
(f(12), f(31), f(53)) = (78, 496, 1431)
(f(16), f(38), f(47)) = (136, 741, 1128)
(f(19), f(39), f(45)) = (190, 780, 1035)
(f(23), f(26), f(52)) = (276, 351, 1378)
(f(33), f(37), f(38)) = (561, 703, 741)
(f(34), f(35), f(39)) = (595, 630, 780)
問題5
f(x) = x2
(f(1), f(2), f(8), f(44)) = (1, 4, 64, 1936)
(f(1), f(2), f(20), f(40)) = (1, 4, 400, 1600)
(f(1), f(8), f(28), f(34)) = (1, 64, 784, 1156)
(f(1), f(14), f(28), f(32)) = (1, 196, 784, 1024)
(f(2), f(2), f(29), f(34)) = (4, 4, 841, 1156)
(f(2), f(4), f(7), f(44)) = (4, 16, 49, 1936)
(f(2), f(4), f(31), f(32)) = (4, 16, 961, 1024)
(f(2), f(8), f(16), f(41)) = (4, 64, 256, 1681)
(f(2), f(10), f(26), f(35)) = (4, 100, 676, 1225)
(f(2), f(13), f(26), f(34)) = (4, 169, 676, 1156)
(f(2), f(14), f(19), f(38)) = (4, 196, 361, 1444)
(f(2), f(16), f(28), f(31)) = (4, 256, 784, 961)
(f(2), f(19), f(22), f(34)) = (4, 361, 484, 1156)
(f(2), f(22), f(26), f(29)) = (4, 484, 676, 841)
(f(3), f(6), f(14), f(42)) = (9, 36, 196, 1764)
(f(3), f(14), f(30), f(30)) = (9, 196, 900, 900)
(f(4), f(4), f(23), f(38)) = (16, 16, 529, 1444)
(f(4), f(7), f(28), f(34)) = (16, 49, 784, 1156)
(f(4), f(9), f(12), f(42)) = (16, 81, 144, 1764)
(f(4), f(10), f(17), f(40)) = (16, 100, 289, 1600)
(f(4), f(12), f(18), f(39)) = (16, 144, 324, 1521)
(f(4), f(16), f(17), f(38)) = (16, 256, 289, 1444)
(f(4), f(17), f(26), f(32)) = (16, 289, 676, 1024)
(f(4), f(18), f(24), f(33)) = (16, 324, 576, 1089)
(f(4), f(23), f(26), f(28)) = (16, 529, 676, 784)
(f(6), f(6), f(13), f(42)) = (36, 36, 169, 1764)
(f(6), f(12), f(12), f(41)) = (36, 144, 144, 1681)
(f(6), f(12), f(15), f(40)) = (36, 144, 225, 1600)
(f(6), f(12), f(23), f(36)) = (36, 144, 529, 1296)
(f(6), f(13), f(30), f(30)) = (36, 169, 900, 900)
(f(7), f(10), f(16), f(40)) = (49, 100, 256, 1600)
(f(7), f(16), f(16), f(38)) = (49, 256, 256, 1444)
(f(7), f(16), f(26), f(32)) = (49, 256, 676, 1024)
(f(7), f(20), f(20), f(34)) = (49, 400, 400, 1156)
(f(8), f(8), f(14), f(41)) = (64, 64, 196, 1681)
(f(8), f(14), f(28), f(31)) = (64, 196, 784, 961)
(f(8), f(16), f(23), f(34)) = (64, 256, 529, 1156)
(f(9), f(12), f(22), f(36)) = (81, 144, 484, 1296)
(f(9), f(18), f(24), f(32)) = (81, 324, 576, 1024)
(f(10), f(10), f(19), f(38)) = (100, 100, 361, 1444)
(f(10), f(14), f(22), f(35)) = (100, 196, 484, 1225)
(f(10), f(16), f(25), f(32)) = (100, 256, 625, 1024)
(f(12), f(12), f(14), f(39)) = (144, 144, 196, 1521)
(f(12), f(14), f(24), f(33)) = (144, 196, 576, 1089)
(f(12), f(18), f(24), f(31)) = (144, 324, 576, 961)
(f(13), f(14), f(14), f(38)) = (169, 196, 196, 1444)
(f(13), f(14), f(22), f(34)) = (169, 196, 484, 1156)
(f(13), f(22), f(26), f(26)) = (169, 484, 676, 676)
(f(14), f(16), f(23), f(32)) = (196, 256, 529, 1024)
(f(14), f(20), f(25), f(28)) = (196, 400, 625, 784)
(f(14), f(22), f(22), f(29)) = (196, 484, 484, 841)
(f(16), f(17), f(26), f(28)) = (256, 289, 676, 784)
(f(18), f(23), f(24), f(24)) = (324, 529, 576, 576)
(f(19), f(22), f(22), f(26)) = (361, 484, 484, 676)
(f(20), f(20), f(23), f(26)) = (400, 400, 529, 676)
問題3について、2005以外の数でも和がその数になるような連続した自然数列を
作っていて気づいたのですが、2, 4, 8, 16, 32, 64, 128, 256, 1024では
数列が作れませんでした。
2nの形の数は2つ以上の連続した自然数の和では表せない?それ以外の数はすべ
て可能?
1より大きい奇数については、2n+1 = n + (n+1)なので全て可能です。

| NO.1510 | 2005.1.17. | Mit | 三角関数と数列(2) |
「オイラーの贈り物」は高校生のときに読んで、数学の楽しさを発見した
思い出のある本です。この数列も印象に残っており、当時はさっぱりわからなかった
のですが、大学時代に複素関数を独習して証明しました。
この数列はうさぎのつがいの問題で有名なフィボナッチ数列になります。
a1 = 1, a2 = 1, a3 = 2, a4 = 3, a5 = 5, ...
an+2 = an+1 + an (n >= 1)
この数列のよく見る一般項は、 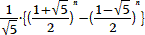 です。
です。
これを使って積表示を証明しています。


| NO.1511 | 2005.1.23. | 水の流れ | 三角形の形状 |
現在、学校で「数学Ⅰ」は三角比ところを、「数学A」では、平面幾何を教えています。この両方の考え方でできそうな問題です。
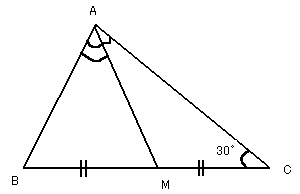
問題:
△ABCの辺BCの中点をMとする。∠C=30°、∠BAM=2∠MACのとき、△ABCはどんな三角形か答えなさい。

| NO.1512 | 2005.1.30. | 佐野允信 | 外接する3円(2) |
小円の中心を、O1、O2とし、中円と大円の中心をそれぞれO3、Oとする。さらに、大円、中円、小円の半径をそれぞれ R、r、tとする。
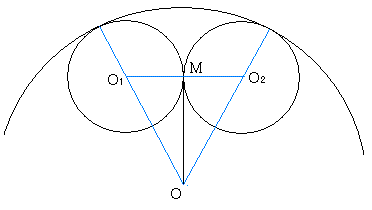
2つの小円は外接するので、接点をMとすると、点Mは線分O1O2の中点である。2つの小円は、大円に内接するので、
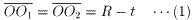
よって、線分OMは、線分O1O2に垂直である。
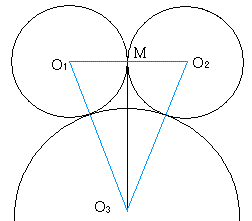
2つの小円は中円と外接するので、
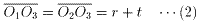
よって、線分O3Oは、線分O1O2に垂直である。
従って、3点O、O3、Mは同一直線上にある。
さらに3点O、O3、Mは、下図のように並んでいる。
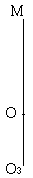
なぜならば、中円は大円に内接し、中円は小円と外接するから。
中円は、大円に内接するから
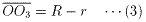
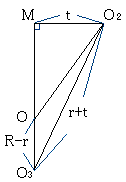
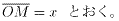
△MOO2について、三平方の定理より
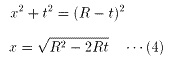
さらに、x>0より、
R>2t ・・・(5)
△MO3O2について、三平方の定理より
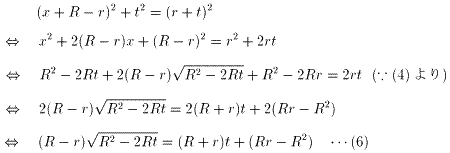
(左辺)>0より、
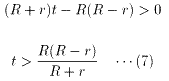
(6)の両辺を2乗すると、
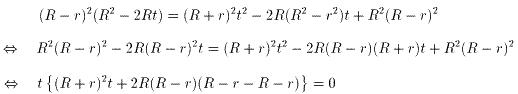
t>0より、
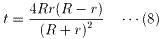
(8)は、(5)を満たさなければならないので、
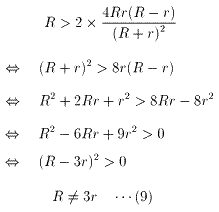
(8)は、(7)を満たさなければならないので、
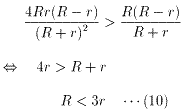
条件より、
2(r-t)=5 ・・・(11)
π(R2-r2-2t2)=120π・・・(12)
ここで、
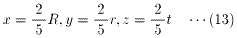
とおくと、(8)、(11)、(12)は、
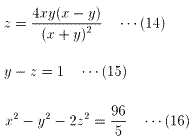
と表せる。
(15)より、
z=y-1 ・・・(17)
(17)を(16)に代入すると
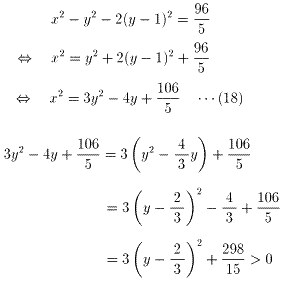
が成り立つ。(18)より、
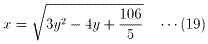
(17)を(14)に代入すると
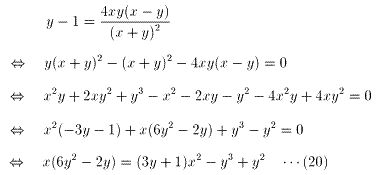
(19)より、
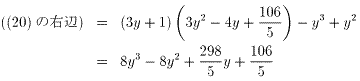
よって、
5x(3y2-y)=20y3-20y2+149y+53 ・・・(21)
(17)より、
z=y-1>0
∴ y>1 ・・・(22)
(22)より、
3y2-y>0 ・・・(23)
(21)、(22)より、
20y3-20y2+149y+53=20y2(y-1)+149y+53>202>0
従って、(21)の両辺は正である。(21)の両辺を2乗して、整理すると
275y6-550y5-915y4+560y3-19551y2ー15794y-2809=0 ・・・(24)
この方程式を解析的に解くことができなかったので、コンピュータを用いて解くと、(22)より、
y≒4.02258972027175 ・・・(25)
(25)を(19)に代入すると
x≒7.32484302165042 ・・・(26)
(25)を(17)に代入すると
z≒3.02258972027175 ・・・(27)
(25)、(26)、(27)を(13)に代入すると
R≒18.312107554126
r≒10.0564743006794
t≒ 7.55647430067937 ・・・(答)

 E-mail
E-mail
 戻る
戻る