| NO.1479 | 2004.9.1. | 悈偺棳傟 | 弴埵寛掕愴 |
丂懢榊偝傫偼丄傾僥僱僆儕儞僺僢僋偺栰媴偺娤愴傪偟偰偄偰丄
梊慖儕乕僌愴曽幃偲寛彑僩乕僫儊儞僩曽幃偺偁傝曽偵媈栤傪懸偪傑偟偨丅
彈巕僜僼僩儃乕儖傒偨偄側儁乕僕僔僗僥儉曽幃側傜偲峫偊偰偟傑偄傑偡丅
丂傕偟丄弴埵偩偗傪寛掕偡傞帋崌傪峴偆偲偡傞偲丄堦懱壗帋崌偑昁梫偵側傞偐峫偊偰傒傑偟偨丅
偱偒傞偩偗彮側偄帋崌悢偱弴埵傪偮偗偨偄偲巚偄傑偡丅
偨偩偟丄師偺傛偆側儖乕儖偱峴偄傑偡丅
丂乮侾乯俙偑俛偵彑偪丄俛偑俠偵彑偭偨偲偒偼丄俙偼俠偵彑偮傕偺偲偡傞丅懄偪丄帋崌傪峴偄傑偣傫丅
丂乮俀乯堷偒暘偗偼側偄傕偺偲偡傞丅
丂乮俁乯奺僠乕儉偛偲偺帋崌悢偺懡偄彮側偄偼峫椂偣偢丄憤帋崌悢偩偗傪嵟彫偵偡傞丅
椺偊偽丄俀僠乕儉偱峴偆偲偒偼柧傜偐偵侾帋崌偱弴埵傪寛掕偱偒傑偡丅偙偙偐傜偑栤戣偱偡丅
丂栤戣侾丗
丂丂俁僠乕儉偺偲偒偼丄嵟掅壗夞偺帋崌偱弴埵傪寛掕偱偒傞偐丅嬶懱揑偵偄傠偄傠側応崌傪峫偊偰偔偩偝偄丅
丂栤戣俀丗
丂丂係僠乕儉偺偲偒偼丄嵟掅壗夞偺帋崌偱弴埵傪寛掕偱偒傞偐丅嬶懱揑偵偄傠偄傠側応崌傪峫偊偰偔偩偝偄丅
丂栤戣俁丗
丂丂俆僠乕儉偺偲偒偼丄嵟掅壗夞偺帋崌偱弴埵傪寛掕偱偒傞偐丅嬶懱揑偵偄傠偄傠側応崌傪峫偊偰偔偩偝偄丅
丂栤戣係丗
丂丂摨偠儖乕儖偱丄乮値亄侾乯僠乕儉偺偲偒偲値僠乕儉偺偲偒偱偼嵟彫憤帋崌悢偺娫偵偼偳傫側幃偑偱偒傞偐丄梊憐偟偰偔偩偝偄丅
捛壛丗偱偒偨傜丄値僠乕儉偺偲偒偼丄嵟掅壗夞偺帋崌偱弴埵傪寛掕偱偒傞偐丅峫偊偰偔偩偝偄丅
亀拲丗儁乕僕僔僗僥儉偲偼丄攕幰暅妶愴傪娷傓僩乕僫儊儞僩偱丄
乽2偮偺僙儈僼傽僀僫儖偲僼傽僀僫儖丄僌儔儞僪僼傽僀僫儖乿偱峔惉偝傟傞丅
1師儕乕僌3埵偲4埵偑戞1僙儈僼傽僀僫儖乮8寧22擔戞1帋崌乯傪峴偄丄攕幰偼4埵妋掕丅
彑幰偼僼傽僀僫儖乮22擔栭偺帋崌乯偵恑弌丅
1師儕乕僌1埵偲2埵偑戞2僙儈僼傽僀僫儖乮22擔戞2帋崌乯傪峴偄丄彑幰偼僌儔儞僪僼傽僀僫儖乮23擔乯傊丅
攕幰偼戞1僙儈僼傽僀僫儖偺彑幰偲僼傽僀僫儖偱懳愴丅
僼傽僀僫儖偱偺攕幰偼3埵乮摵儊僟儖乯妋掕丅彑幰偼僌儔儞僪僼傽僀僫儖傊丅
僌儔儞僪僼傽僀僫儖偼寛彑愴偱丄彑幰偑桪彑乮嬥儊僟儖乯丄攕幰偑弨桪彑乮嬧儊僟儖乯妋掕丅

| NO.1480 | 2004.9.2. | Junko | 幨憸偲悢楍(2) |
偙傟偼乽慺場悢暘夝乿偺榖偱偡偹丅
(1)n偑2埲忋偺慺悢偱偁傞偲偒丄n偑師偺傛偆偵慺場悢暘夝偝傟偰偄偨偲偟傑偡丅
丂丂丂丂n=p1丒p2丒p3丒丒丒pk
偨偩偟丄pi偼慺悢丄偐偮丂p1亞p2亞p3亞丒丒丒亞pk亜1偲偟傑偡丅
(i)傛傝丄
| f(n) | =f(p1丒p2丒p3丒丒丒pk) |
| =max{f(p1),f(p2),f(p3),丒丒丒,f(pk)} | |
| =max{p1,p2,p3,丒丒丒,pk}丂丂丂丂丂[pi偼丄慺悢側偺偱丄(ii),(iii)傛傝丄f(pi)=pi] | |
| =p1 |
偮傑傝丄f(n)偼丄n傪妱傝愗傞嵟戝偺慺悢偲側傞丅
(2)2埲忋偺帺慠悢偱偁傞a1偑丄師偺傛偆偵慺場悢暘夝偝傟偰偄偨偲偟傑偡丅
丂丂丂丂a1=p1丒p2丒p3丒丒丒pk
偨偩偟丄pi偼慺悢丄偐偮丂p1亞p2亞p3亞丒丒丒亞pk亜1偲偟傑偡丅
偙偺偲偒丄f(a1)=p1偱偡偐傜丄a2=a1/p1=p2丒p3丒丒丒pk
師偵丄f(a2)=p2偱偡偐傜丄a3=a2/p2=p3丒p4丒丒丒pk
摨條偵丄f(a3)=p3偱偡偐傜丄a4=a3/p3=p4丒p5丒丒丒pk
丒丒丒
ak=pk
ak+1=ak/pk=1傛傝丄f(ak+1)=1
ak+2=ak+3=丒丒丒=1丂偐偮丂f(ak+2)=f(ak+3)=丒丒丒=1
n亜k偲峫偊偰傛偄偐傜丄
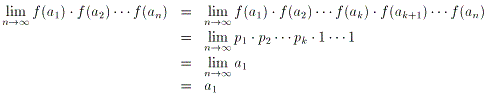

| NO.1481 | 2004.9.5. | 杮懡嬘椇 | 暥妛揑側栤戣(1) |
暥妛揑側栤戣乮乽悘敽乿偲乽攩乿偭偰僯儏傾儞僗偑偳偆堘偆偺丠乯
悢妛梡岅偱乽悘敽峴楍乿偲乽攩娭悢乿偲偄偆梡岅偑偁傝傑偡丅
偄偢傟傕丄乽乣偐傜摫弌偝傟傞乿乽乣偲堦弿偵側偭偰偄傞乿乽乣偺曗彆揑側乿偺
傛偆側堄枴偑偁傠偆偐偲巚偄傑偡偑丄偙偺曈偺擔杮岅偺栿岅丒梡岅偺嵦梡寛掕偵
帄偭偨楌巎揑宱堒側偳屼懚抦偺曽丄偤傂嫵偊偰偔偩偝偄丅
仸島媊偱丄攩娭悢偲偄偆帤傪斅彂偟偨傜乽愭惗両攞娭悢偺岆傝偠傖側偄傫偱偡偐
丠乿偲幙栤偟偨妛惗偑偍偭偨偲偐丅擔忢巊傢側偄傛偆側擄夝側岅嬪丒娍帤偼丄堄
枴傪柧妋偵愢柧丒棟夝偟側偄偲偄偗側偄側偀偲巚偭偰偍傝傑偡丅

| NO.1482 | 2004.9.12. | yokodon | 暥妛揑側栤戣(2) |
Google 偱挷傋偰傒傑偟偨丅偙偺擔杮岅偺梡岅偑嵦梡偝傟傞偵帄偭偨楌巎揑宱堒偼 傛偔暘偐傝傑偣傫偑丄 搶嫗擾岺戝妛嵅摗尋媶幒偺儁乕僕 偵傛傟偽丄
乽攩娭悢偲偄偆偺偼 associated function 偺栿偱丄摨敽娭悢丄悘敽娭悢 丄廬娭悢側偳偲栿偝傟偰偄傑偡丅暿偺娭悢偐傜旝暘傗愊暘偺宍偱梌偊傜傟傞傛偆側娭 悢偲偄偆堄枴乿側偺偩偦偆偱偡丅

| NO.1483 | 2004.9.12. | yokodon | 幨憸偲悢楍(3) |
NO.1480 傪攓尒偟傑偟偨丅嬄傞捠傝丄慺場悢暘夝偑戣嵽偱偡丅
婰朄傪曄偊偰丄慺悢偲偼尷傜側偄帺慠悢 n 偺慺場悢暘夝偺昞婰偑丄
慺悢傪 p1 亜p2 亜...亜 pk (亞 1) 偲偟丄
旕晧惍悢傪 b1, b2, ..., bk 偲偟偰丄
丂丂丂丂n 亖p1b1丒p2b2丒...丒pkbk
偲弌棃傞偙偲傪梡偄傟偽丄
栤乮1乯偼
| f(n) | 亖 max{f(p1b1), f(p2b2), ..., f(pkbk)} |
| 亖 f(pjbj) 丂丂乮偙偙偵丄bj 偼 bi (i 亖 1, 2, ..., k) 偺拞偱丄嵟弶偵尰傟傞 0 偱側偄傕偺乯 | |
| 亖 max{f(pj), f(pj), ...f(pj)} 丂丂乮max{丂} 偺拞偵 bj 屄偺 f(pj) 偑偁傞乯 | |
| 亖 f(pj) | |
| 亖 pj |
偺條偵傕弌棃傑偡丅
庒偟偔偼丄f(n) 偺堷悢 n 偵娭偡傞悢妛揑婣擺朄偱傕帵偡偙偲偑弌棃傑偡丅
丂屻敿偺栤乮2乯偵娭偟偰偼丄an+1 亖 an/f(an) 偺娭學幃傪梡偄傞偲
丂丂丂丂f(a1)丒f(a2)丒...丒f(an) 亖 a1/an+1
丒丒丒偱偡偐傜丄
丂丂丂丂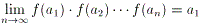
偼丄寢嬊
丂丂丂丂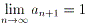
偲摨抣偱偡丅偙傟傪帵偣偽傛偄傢偗偱偡丅
丂偲偙傠偑丄忋婰偺傛偆偵
丂丂丂丂n 亖p1b1丒p2b2丒...丒pkbk
偲偍偗傞偲偡傞偲丄NO.1480 偺Junko偝傫偺媍榑偲摨條偵偟偰丄廩暘戝偒側桳尷偺 n 偵
偍偄偰乮嬶懱揑偵偼丄n 亞 b1 + b2 +...+ bk + 1 偺偲偒乯an 亖 1 偲側傞偙偲
傪帵偣傑偡丅
丂偙傟傕丄a1 偑 m 屄偺帺慠悢偱昞偣傞偲偟偰丄m 偵娭偡傞悢妛揑婣擺朄傪梡偄偰
帵偡偙偲偑弌棃傑偡丅
#摨媊斀暅偵側偭偰偟傑偄傑偟偨丅

| NO.1484 | 2004.9.12. | yokodon | 壜姺側峴楍偺慡懱(1) |
嵟嬤丄僶僀僩愭偱偙傫側栤戣偵憳嬾偟傑偟偨丅
乵栤戣乶
丂梌偊傜傟偨幚俀師惓曽峴楍俙偵懳偟偰丄僛儘峴楍偱側偄偁傞幚俀師惓曽峴楍倃偑懚嵼偟丄
- 俙倃亖倃俙
- 偁傞幚悢 p, q 傪梡偄偰丄倃亖p俙+q俤 偲昞偣傞乮俤丟俀師扨埵峴楍乯丅
- 偙偺宍偵側傜側偄倃偼懚嵼偟側偄丅
...偺俁偮偑惉傝棫偮偨傔偺俙偵娭偡傞忦審傪媮傔傛丅
丂偙偺栤戣偦偺傕偺偺摎偊偼乽俙偑扨埵峴楍偺掕悢攞偱側偄偙偲乿側偺偱偡偑丄偙傟
傪堦斒偺 n 師惓曽峴楍偺応崌偵奼挘偟偨傜偳偆側傞偺偩傠偆丠偲偄偆媈栤偑桸偒傑
偟偨丅n 亖 2 偺応崌偼乮傗傗庤娫偺偐偐傞乯惉暘寁嶼傪宱偰寢榑偵偨偳傝拝偗傑偡
乮#嫽枴偺偁傞曽偼偍帋偟傪乯丅偑丄n 亞 3 偺応崌偼丄惉暘寁嶼偱偼僪僣儃偱偡丅
丂擮偺偨傔丄梊憐傕娷傔偰乮栤戣偦偺傕偺偺揔晄揔偼搙奜帇偟偰乯夵傔偰栤戣傪婰偡
偲丄偙傫側姶偠偱偟傚偆偐丅
乵栤戣乶
丂梌偊傜傟偨幚 n 師惓曽峴楍俙偵懳偟偰丄僛儘峴楍偱側偄偁傞幚 n 師惓曽峴楍倃偑
懚嵼偟丄
- 俙倃亖倃俙
- 偁傞幚悢 pk (k 亖 0, 1,.., n)傪梡偄偰丄倃亖儼pk丒俙k 偲昞偣傞丅
丂乮榓偼丄k丗0 仺 n丟側偍丄俙0 亖 俤(丟n 師扨埵峴楍) 偲偡傞乯 - 偙偺宍偵側傜側偄倃偼懚嵼偟側偄丅
...偺俁偮偑惉傝棫偮偨傔偺俙偵娭偡傞忦審傪媮傔傛丅
乵寢壥偺梊憐乶
丂俙偑扨埵峴楍偺掕悢攞偱側偄偙偲丅
丂惉暘寁嶼偱偼墴偟恑傔偑偨偄偲側傞偲丄慄宍戙悢傪抦偭偰偄傞幰偲偟偰偼丄堦斒儀
僋僩儖嬻娫偺媍榑傪峫偊傞偺偑帺慠偱偟傚偆偐丅梌偊傜傟偨峴楍俙偵懳偟偰丄偦傟偲
乮捠忢偺峴楍偺乯愊偵娭偟偰壜姺側峴楍倃偑昁偢懚嵼偡傞偙偲傪帵偡偺偼丄俙倃亖倃
俙偺幃傪俛[x] 亖 [0]乮塃婰偱丄[x] 偼峴楍倃偺惉暘傪慡偰廲偵暲傋偨 n2 師尦儀
僋僩儖丄[0] 偼 n2 師尦僛儘儀僋僩儖丄俛偼偁傞 n2 師惓曽峴楍乯偺宍偵偟偨偲偒
丄det(俛)亖0乮幚偼丄rank(俛) 亙 n2乯偑昁偢惉傝棫偮偙偲傪帵偣偽椙偄偺偱丄斾
妑揑娙扨偦偆側姶偠偱偡乮堦斒偺応崌偼寁嶼偑柺搢廘偦偆偱偡偑丟偟偐傕丄rank(俛)
亙 n2 偼...尰抜奒偺杔偺拞偱偼...梊憐偺堟偱偡乯丅
丂栤戣偼屻敿偱偡丅峴楍偺懡崁幃倃亖儼pk丒俙k乮榓偼丄k丗0 仺 n乯偵偍偄偰丄俙
偑扨埵峴楍偺幚悢攞偱側偗傟偽丄{俙k}(k 亖 0, 1, ..., n) 偼乬慄宍撈棫乭乮#儂
儞僩偐側丠乯側偺偱丄幚 n 師惓曽峴楍偺慡懱俵n(俼) 偵娭偟偰丄倃偺慡懱偼偙傟偺
慄宍晹暘嬻娫乮俽偲柤晅偗傑偡乯傪側偡偙偲偑暘偐傝傑偡乮#懡暘...乯丅偦偺倃偺拞
偱丄俙倃亖倃俙傪枮偨偡傕偺偺慡懱乮俿偲柤晅偗傑偡乯偑嬻偱側偔丄俿偑俽偺恀晹暘
廤崌偱偁傞偙偲偑尵偊傟偽椙偝偦偆偱偡丅偟偐偟丄偳偆傗偭偰偙偺媍榑傪恑傔傟偽傛
偄偺偱偟傚偆偐丠
丂忋婰偺梊憐偵懳偡傞斀椺偺懚嵼傕婥偑偐傝側偲偙傠偱偡丅
丂杮審偵娭偟偰偼丄敊慠偲偟偨栤戣堄幆偩偗側傜悢擭棃偁偭偨偲偙傠偱偡偑丄恀柺栚
偵庢傝慻傫偩偙偲偑側偄傕偺偱丄媣乆偵戝巚埬傪廳偹偰丄忋婰偺傛偆偵偮偭偐偊偰偍
傝傑偡丅
丂嫽枴傪偍帩偪偺曽偑偄傜偭偟傖偭偨傜丄専徹偟偰偄偨偩偗傞偲桳傝擄偄偱偡丅

| NO.1485 | 2004.9.18. | DDT | 幚悢偺傾僀僨傾 |
丂楢懕検傪昞偡幚悢偺奣擮偼丄杮棃旕忢偵捈姶揑偱暘偐傝傗偡偄傕偺偩偲巚偄傑偡丅
偪傚偭偲偱傕悢帤偵嫽枴偺偁偭偨恖側傜丄暘悢乮桳棟悢乯傪抦偭偨偲偒偵丄
偦傟偑楢懕検傪昞偡傕偺偩偲敊慠偲梊姶偟偨偼偢偱偡丅
捠忢惓幃側幚悢偲偺弌夛偄偼丄弶傔偰崟斅偵乽 仺 乿乮x幉乯偑尰傟丄乽 仺 乿傪悢捈慄偲屇傃丄
偙偺忋偺揰偑楢懕検傪昞偡偲嫵偊傜傟偨帪偱偡丅
偦偟偰丄帋偟偵帺慠悢傪偙偺忋偵昞偡偲偙偆側傞傛偲丄
悢捈慄忋偵帺慠悢偑栚惙傜傟偨弖娫偵桳棟悢偑楢懕検傪昞偡偲偄偆丄偙偺梊姶偼寛掕揑偵側偭偨偼偢偱偡丅
偮傑傝敪憐偺尨揰偼暔嵎偟偱偡丅偲偙傠偑師偵丄
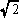 偼桳棟悢偱側偄偲尵傢傟傑偡丅偦傟傕攚棟朄傪巊偭偨岻柇側曽朄偱丅
巚偆偵偙偺帪揰偱偼晛捠丄攚棟朄側偳偲偄偆徹柧偵偼姷傟偰偍傜偢撪梕傕傠偔偵傢偐傝傑偣傫丅
恖娫婥帩偪偺埆偄暔傗搒崌偺埆偄帠偼柍帇偟偑偪偱偡丅
偼桳棟悢偱側偄偲尵傢傟傑偡丅偦傟傕攚棟朄傪巊偭偨岻柇側曽朄偱丅
巚偆偵偙偺帪揰偱偼晛捠丄攚棟朄側偳偲偄偆徹柧偵偼姷傟偰偍傜偢撪梕傕傠偔偵傢偐傝傑偣傫丅
恖娫婥帩偪偺埆偄暔傗搒崌偺埆偄帠偼柍帇偟偑偪偱偡丅
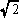 偑桳棟悢偱側偄偺偼壗偐婬桳偺椺奜偺傛偆側傕偺偱丄
怺崗偵婥偵偡傞偙偲偼側偄偲偄偆婥暘偵側傝傑偡偑丄
偙偺偲偒乽桳棟悢 亖 楢懕検乿偲偄偆恾幃偑彮偟偩偗偖傜偮偒傑偡丅寛掕懪傪怘傜偆偺偼傕偆彮偟屻偱偡丅
桳棟悢偼幚悢捈慄傪寗娫側偔杽傔恠偔偡偺偵乮忢幆揑側堄枴偱乯丄
偦偺柍偄偼偢偺寗娫偵丄側偍傕柍悢偺柍棟悢偑偁傞偲尵傢傟偨帪偱偡丅
偙偺帪揰偱乽暔嵎偟 亖 桳棟悢 亖 楢懕検乿偲偄偆恾幃偑傕偼傗堐帩偱偒側偄傕偺偲丄怱偺偳偙偐偱妎屽偟傑偡丅
幚悢偑撍慠惓懱晄柧側壗偐偵壔偗傑偡丅偱傕幚嵺忋偼丄媽棃偺敪憐偱寁嶼傕壗傕曅晅偔偺偱丄
昞柺忋偙偲偼惷壐偵悇堏偟傑偡丅
偑桳棟悢偱側偄偺偼壗偐婬桳偺椺奜偺傛偆側傕偺偱丄
怺崗偵婥偵偡傞偙偲偼側偄偲偄偆婥暘偵側傝傑偡偑丄
偙偺偲偒乽桳棟悢 亖 楢懕検乿偲偄偆恾幃偑彮偟偩偗偖傜偮偒傑偡丅寛掕懪傪怘傜偆偺偼傕偆彮偟屻偱偡丅
桳棟悢偼幚悢捈慄傪寗娫側偔杽傔恠偔偡偺偵乮忢幆揑側堄枴偱乯丄
偦偺柍偄偼偢偺寗娫偵丄側偍傕柍悢偺柍棟悢偑偁傞偲尵傢傟偨帪偱偡丅
偙偺帪揰偱乽暔嵎偟 亖 桳棟悢 亖 楢懕検乿偲偄偆恾幃偑傕偼傗堐帩偱偒側偄傕偺偲丄怱偺偳偙偐偱妎屽偟傑偡丅
幚悢偑撍慠惓懱晄柧側壗偐偵壔偗傑偡丅偱傕幚嵺忋偼丄媽棃偺敪憐偱寁嶼傕壗傕曅晅偔偺偱丄
昞柺忋偙偲偼惷壐偵悇堏偟傑偡丅
偝偰戝妛偵擖偭偨偲偟傑偡丅戝妛偺庼嬈偵偼丄幚悢偺惓懱偵墳偊偰偔傟傞柧夣側夝摎偑梡堄偝傟偰偄傞偵堘偄側偄両丅
恖偵傛傞偲偼巚偄傑偡偑丄偦傫側偙偲偼偁傝傑偣傫両丅
偄傢偔乽僨僨僉儞僩偺愗抐偑幚悢偺楢懕惈傪昞偡乿丄偄傢偔乽暵嬫娫偺尭彮楍偼嬻偱側偄乮幚悢偺楢懕惈乯乿丄
傑偨偼乽僐乕僔乕楍偺摨抣椶偵傛傞幚悢偺峔惉乿側偳偱偡丅
乽暔嵎偟 亖 桳棟悢 亖 楢懕検乿偲偄偆扨弮柧夣側恾幃偐傜偼丄偳傫偳傫偐偗棧傟偰偄偒傑偡丅
偱傕偙偺恾幃偼丄偦傫側偵娫堘偄側傫偱偟傚偆偐丠丅幚悢傪堚楻柍偔峔惉偟傛偆偲巚偆偲丄
姰旛惈偲偐摨抣椶偲偐偺奣擮揑嫴嶨暔乮昁梫偱偁傝揔惓側悢妛揑摴嬶棫偰側偺偱偡偑乯偑慜柺偵弌偰偒偰丄
偳偆偟偰傕尨揰偺傾僀僨傾偑夃傒傑偡丅偱傕乽暔嵎偟 亖 桳棟悢 亖 楢懕検乿偺恾幃偼丄偦傟傜悢妛揑摴嬶棫偰偺屻傠偱丄
嵟屻傑偱惗偒偰偄傞偲巚偄傑偡丅埲壓幚悢偺峔惉偺僗働僢僠傪帋傒傑偡丅
侾丏暔嵎偟偲桳棟悢
 尨巒揑側暔嵎偟偺僀儊乕僕偼塃恾偺傛偆側傕偺偩偲巚偄傑偡丅
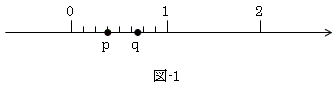
摍娫妘偵扨埵嫍棧0丆1丆2丆丒丒丒傪暲傋丄偦偺拞娫偵偁傞揰p傪昞偡偨傔偵丄扨埵嫍棧偺娫偵曗彆栚惙傪愝偗傑偡丅
偙偙偱曗彆栚惙偺偲傝曽偼擟堄偱偡偑丄摍暘妱偑尨懃偱偡丅恾-1偱偼揰p偼丄3/8偲側傝傑偡丅
曗彆栚惙偺拞娫偵偔傞揰q偺傛偆側応崌傕摨偠偱偡丅
曗彆栚惙偺偲傝曽偼擟堄側偺偱丄傕偭偲嵶偐偄曗彆栚惙娫妘傪巊偄傑偡丅椺偊偽1/16偲偐丅
偙偙偱丄嵦梡偟偨曗彆栚惙娫妘傪1/n偱昞偟乮n偼0偱側偄帺慠悢乯丄1/n傪暘妱扨埵丆偦偺暘曣値傪暘妱偲屇傫偱偍偒傑偡丅
尨巒揑側暔嵎偟偺僀儊乕僕偼塃恾偺傛偆側傕偺偩偲巚偄傑偡丅
摍娫妘偵扨埵嫍棧0丆1丆2丆丒丒丒傪暲傋丄偦偺拞娫偵偁傞揰p傪昞偡偨傔偵丄扨埵嫍棧偺娫偵曗彆栚惙傪愝偗傑偡丅
偙偙偱曗彆栚惙偺偲傝曽偼擟堄偱偡偑丄摍暘妱偑尨懃偱偡丅恾-1偱偼揰p偼丄3/8偲側傝傑偡丅
曗彆栚惙偺拞娫偵偔傞揰q偺傛偆側応崌傕摨偠偱偡丅
曗彆栚惙偺偲傝曽偼擟堄側偺偱丄傕偭偲嵶偐偄曗彆栚惙娫妘傪巊偄傑偡丅椺偊偽1/16偲偐丅
偙偙偱丄嵦梡偟偨曗彆栚惙娫妘傪1/n偱昞偟乮n偼0偱側偄帺慠悢乯丄1/n傪暘妱扨埵丆偦偺暘曣値傪暘妱偲屇傫偱偍偒傑偡丅
n偼擟堄側偺偱丄幚嵺偄偔傜偱傕嵶偐偄曗彆栚惙傪巊偊傑偡丅
昁梫偵墳偠偰曗彆栚惙傪偳傫偳傫嵶偐偔偟偰偄偗偽乮暘妱傪戝偒偔偟偰偄偗偽乯丄
悢捈慄忋偺偳傫側揰傕昞偣傞偵堘偄側偄丅偡側傢偪廫暘戝偒側n傪偲傟偽丄擟堄偺幚悢偼丄
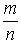 丂丂丂丂丂丂丂丂丂(1)
丂丂丂丂丂丂丂丂丂(1)
俀丏桳棟悢丆彫悢揥奐丆弞娐彫悢
丂桳棟悢偵偍偄偰偼丄暘妱扨埵乮曗彆栚惙娫妘乯偼擟堄偱偟偨丅暘妱扨埵傪擟堄偵偲傟傞偲偙傠偑桳棟悢偺曋棙偝偱偡偑丄
摨帪偵崿棎偺傕偲偵傕側傝傑偡丅偦偙偱暘妱偺寛傔曽傪1偮偵屌掕偟丄桳棟悢昞尰傪僔僗僥儉壔偟偨傕偺偑丄
幚悢偺彫悢揥奐偩偲偄偊傑偡丅
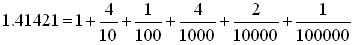 丂丂丂丂丂丂丂丂丂(2)
丂丂丂丂丂丂丂丂丂(2)
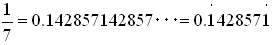 丂丂丂丂丂丂丂丂丂(3)
丂丂丂丂丂丂丂丂丂(3)
掕棟侾丂
擟堄偺桳棟悢偼弞娐彫悢丅
乵徹柧乶
幃(3)嵍曈偺妱傝嶼傪昅嶼偱捛偄偐偗傞偲傢偐傞偑丄摨偠梋傝偑弌偨帪揰偱埲壓摨偠寁嶼偲側傝丄彜偺弞娐偑巒傑傞丅
傛偭偰桳棟悢傪彫悢偵捈偡彍嶼偵偍偄偰丄昁偢摨偠梋傝偑尰傟傞偙偲傪尵偊偽椙偄丅
桳棟悢傪丄
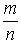
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乵徹柧廔傢傝乶
丂掕棟侾偵偍偄偰杮幙揑側偺偼丄暘曣値偑帺慠悢偱偁傝昁偢桳尷偱偁傞偙偲偲丄 慏宍寁嶼偼偄偔傜偱傕懕偗傜傟傞偙偲偱偡乮椺偊偽妱傝愗傟偰傕丄梋傝0傪偄偔傜偱傕妱傝懕偗傞偙偲偑偱偒傞乯丅 偙傟偼杮幙揑側偙偲偱丄師偺
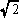 偺彫悢揥奐偲斾妑偡傞偲丄偦偺埵抲偯偗偑偼偭偒傝偟傑偡丅
偺彫悢揥奐偲斾妑偡傞偲丄偦偺埵抲偯偗偑偼偭偒傝偟傑偡丅俁丏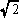 偺彫悢揥奐丆桳尷偱偁傞偲偄偆偙偲丄柍尷偱偁傞偲偄偆偙偲
偺彫悢揥奐丆桳尷偱偁傞偲偄偆偙偲丄柍尷偱偁傞偲偄偆偙偲
丂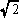 偼桳棟悢偱偼偁傝傑偣傫丅
偦偺徹柧偼丄
偼桳棟悢偱偼偁傝傑偣傫丅
偦偺徹柧偼丄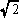 傪婛栺暘悢q/p偱昞傢偣傞偲偟偨応崌丄
p偑嬼悢側傜q偼婏悢偱側偗傟偽側傜側偄偑丄2亖q2/p2 佀 2p2亖q2偐傜q偼嬼悢丆
p偑婏悢側傜q偼嬼悢偱側偗傟偽側傜偢丄p偼2偱妱傝愗傟偰偼偄偗側偄偑丄
2亖q2/p2 佀 2p2亖q2 佀 p2亖q2/2 偐傜
p偼2偱妱傝愗傟傞偺偱柕弬丆
廬偭偰丄婛栺側帺慠悢q偲p偱
傪婛栺暘悢q/p偱昞傢偣傞偲偟偨応崌丄
p偑嬼悢側傜q偼婏悢偱側偗傟偽側傜側偄偑丄2亖q2/p2 佀 2p2亖q2偐傜q偼嬼悢丆
p偑婏悢側傜q偼嬼悢偱側偗傟偽側傜偢丄p偼2偱妱傝愗傟偰偼偄偗側偄偑丄
2亖q2/p2 佀 2p2亖q2 佀 p2亖q2/2 偐傜
p偼2偱妱傝愗傟傞偺偱柕弬丆
廬偭偰丄婛栺側帺慠悢q偲p偱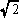 亖q/p偲昞偡偙偲偼晄壜擻丄偲側傞丅
亖q/p偲昞偡偙偲偼晄壜擻丄偲側傞丅
丂偙偺徹柧偺堄枴偼偝偰偍偔偲偟偰丄寢壥傪擣傔傟偽 掕棟侾 傛傝
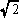 偼丄弞娐彫悢偱偼側偄偙偲偵側傝傑偡丅
弞娐彫悢偱偼側偄偲偼丄弞娐偟側偄柍尷彫悢偺偙偲偱偡丅偲傝偁偊偢偙傟偩偗偼擣傔丄
偼丄弞娐彫悢偱偼側偄偙偲偵側傝傑偡丅
弞娐彫悢偱偼側偄偲偼丄弞娐偟側偄柍尷彫悢偺偙偲偱偡丅偲傝偁偊偢偙傟偩偗偼擣傔丄
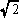 偺桳棟悢嬤帡傪峴偭偰傒傑偡丅
偺桳棟悢嬤帡傪峴偭偰傒傑偡丅
丂
丂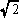 偺桳棟悢嬤帡(4)偵偍偄偰丄彫悢晹暘偺暘妱扨埵1/n偵拲栚偟傑偡丅
椺偊偽(4)偺2峴栚偼丄0.4傪昞偡偺偵暘妱扨埵1/5偑昁梫偩偲尵偭偰傑偡丅
暘妱扨埵偺暘曣丄暘妱偲屇傇偙偲偵偟偨値偼丄
値亖5丆100丆500丆1250丆100000丆1000000丆2000000丆25000000丆丒丒丒 偲丄
彫悢偺嬤帡寘悢偑忋偑傞偵廬偭偰憹壛偟偰偄偒傑偡丅偳偙傑偱憹壛偡傞偐偲偄偆偲丄
偙傟偵偼廔傢傝偑偁傝傑偣傫丅弞娐偟側偄柍尷彫悢偺暘妱値偺憹壛偵尷傝偑柍偄偙偲偼丄
師偺傛偆偵娙扨偵徹柧偱偒傑偡丅
偺桳棟悢嬤帡(4)偵偍偄偰丄彫悢晹暘偺暘妱扨埵1/n偵拲栚偟傑偡丅
椺偊偽(4)偺2峴栚偼丄0.4傪昞偡偺偵暘妱扨埵1/5偑昁梫偩偲尵偭偰傑偡丅
暘妱扨埵偺暘曣丄暘妱偲屇傇偙偲偵偟偨値偼丄
値亖5丆100丆500丆1250丆100000丆1000000丆2000000丆25000000丆丒丒丒 偲丄
彫悢偺嬤帡寘悢偑忋偑傞偵廬偭偰憹壛偟偰偄偒傑偡丅偳偙傑偱憹壛偡傞偐偲偄偆偲丄
偙傟偵偼廔傢傝偑偁傝傑偣傫丅弞娐偟側偄柍尷彫悢偺暘妱値偺憹壛偵尷傝偑柍偄偙偲偼丄
師偺傛偆偵娙扨偵徹柧偱偒傑偡丅
掕棟俀丂
丂弞娐偟側偄柍尷彫悢偵昁梫側暘妱値偼丄桳尷偱側偄乮尷傝偑柍偄乯丅
乵徹柧乶
丂弞娐偟側偄柍尷彫悢s偵昁梫側暘妱値偑桳尷偩偲偡傞丅値偑桳尷側偺偱丄s偼丄
丂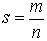 丂丂丂丂丂丂丂丂丂丂丂(5)
丂丂丂丂丂丂丂丂丂丂丂(5)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乵徹柧廔傢傝乶

丂掕棟2 偺徹柧偵丄偁傞庬偺嫊偟偝傪姶偠傞偺偼巹偩偗偱偼側偄偲巚偄傑偡丅壗偑嫊偟偄偐偲偄偆偲丄
壗屘弞娐偟側偄柍尷彫悢偵偍偄偰暘妱値偑偳傫偳傫戝偒偔側傞偐傪丄掕棟1偺傛偆偵嬶懱揑側彍嶼傪揥奐偟偰岅偭偰偄側
偄偐傜偱偡丅掕棟2偼偦偆偡傞偐傢傝偵攚棟朄傪梡偄傑偡丅攚棟朄傪梡偄偢偵丄昁梫暘妱値偑尷傝側偔戝偒偔側傞偙偲傪
徹柧偡傞偙偲乮峔惉揑偵徹柧偡傞偙偲乯偼丄幚偼偱偒傑偣傫丅棟桼偼偁偒傟傞傎偳娙扨偱丄弞娐偟側偄柍尷彫悢偵懳偟偰
恾-2偵傛偆側廙宍寁嶼傪幚峴偟傛偆偲偟偨応崌丄妱傞悢値乮恾-2偱偼7乯偑 亣 偵側偭偰偟傑偄丄偳傫側悢抣寁嶼偵傕
嵹傜側偄偐傜偱偡丅壗屘 亣 偵懳偟偰偼丄傑偲傕側悢抣寁嶼偑偱偒側偄偺偐丠丅亣 偵偼傑偲傕側悢抣揑惈幙傪掕媊偱
偒側偄偐傜偱偡丅偦傟偼偳偆偟偰偐丠丅悢抣揑惈幙傪掕媊偡傞偨傔偵偼丄扤偐偑 亣 傪1夞偼尒傞昁梫偑偁傝傑偡丅
偲偙傠偑丄亣 偼扤傕尒偨偙偲偑偁傝傑偣傫丅壗屘尒傟側偄偺偐丠丅傕偟扤偐偑尒傟偰偟傑偭偨傜丄偦傟偼桳尷偩偐傜偱偡丅
NO.1476偺嵟屻偐傜5峴栚傪堷梡偟傑偡丅
廤崌偑柍尷偱偁傞偲偼丄偦傟偑桳尷偱側偄偙偲傪偄偆丏丂丂丂丂丂丂丂(6)
偐傜偱偡丅偙傟偑柍尷偺掕媊偱偡丅尒傟偨傜桳尷側偺偱丄帺慠悢偺堦偮偵側偭偰偟傑偆偲偄偭偰傕摨偠偱偡丅
掕棟2偼丄杮棃摓払偱偒側偄応崌偺偙偲傪徹柧偟傛偆偲偟偰偄傑偡丅掕棟2傪攚棟朄偵傛傜側偄偱徹柧偡傞偙偲偼丄
杮幙揑偵偱偒側偄傢偗偱偡丅偦傟偼丄柍尷廤崌偺掕媊(6)偦偺傕偺偑曐徹偟傑偡丅
柍尷偵娭偡傞攚棟朄徹柧偺婥帩偪埆偝偼丄偡傋偰(6)偵抂傪敪偟偰偄傞偲丄杔偼巚偭偰偄傑偡丅
偦偺戙昞奿偼丄傕偪傠傫僇儞僩儖偺懳妏慄榑朄偱偡乮屻弎乯丅
偲偙傠偱掕棟2偼丄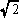 偵娭偟偰 亣 偺暘妱偑昁梫偩偲尵偭偰偄傑偡丅
偙傟傪擣傔傞偲丄偙偺愡偺朻摢偱偁偘偨徹柧偺夝庍偼偳偆側傞偱偟傚偆丠丅
偦傟偼
偵娭偟偰 亣 偺暘妱偑昁梫偩偲尵偭偰偄傑偡丅
偙傟傪擣傔傞偲丄偙偺愡偺朻摢偱偁偘偨徹柧偺夝庍偼偳偆側傞偱偟傚偆丠丅
偦傟偼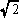 偑婛栺暘悢q/p偱昞偣傞偲偄偆壖掕偺傕偲偱巒傑傝傑偟偨丅
掕棟2偵傛傟偽丄p亖亣 偲偄偆偺偑偦偺寢壥偱偡丅亣 偵懳偟偰嬼悢偩丄婏悢偩偲偄偆偺偼堄枴傪帩偮偺偱偟傚偆偐丠丅
亣 偵偼傑偲傕側悢抣揑惈幙傪掕媊偱偒側偄丄偲偝偭偒尵偄傑偟偨丅
偑婛栺暘悢q/p偱昞偣傞偲偄偆壖掕偺傕偲偱巒傑傝傑偟偨丅
掕棟2偵傛傟偽丄p亖亣 偲偄偆偺偑偦偺寢壥偱偡丅亣 偵懳偟偰嬼悢偩丄婏悢偩偲偄偆偺偼堄枴傪帩偮偺偱偟傚偆偐丠丅
亣 偵偼傑偲傕側悢抣揑惈幙傪掕媊偱偒側偄丄偲偝偭偒尵偄傑偟偨丅
 亖q/p偲壖掕偡傞朻摢偺徹柧偑柕弬偡傞偺偼丄傑偝偵偙偺偙偲傪尵偭偰偄傑偡丅
(4)傪尒傟偽傢偐傞傛偆偵丄暘妱値偼丄昁梫偵墳偠偰嬼悢偵傕婏悢偵傕側傝傑偡丅偦偟偰偙傟偼妋掕偟傑偣傫丅
亖q/p偲壖掕偡傞朻摢偺徹柧偑柕弬偡傞偺偼丄傑偝偵偙偺偙偲傪尵偭偰偄傑偡丅
(4)傪尒傟偽傢偐傞傛偆偵丄暘妱値偼丄昁梫偵墳偠偰嬼悢偵傕婏悢偵傕側傝傑偡丅偦偟偰偙傟偼妋掕偟傑偣傫丅
係丏埫栙偺壖掕
偙偙傑偱偺忬嫷傪傑偲傔偰傒傑偡丅
1) 楢懕検傪昞偡偨傔偵桳棟悢傪摫擖偟偨丅乽暔嵎偟 亖 桳棟悢 亖 楢懕検乿偱偁傞丅
2) 偟偐偟桳棟悢偱偼昞偣側偄悢側偳偑偁傞丅偟偐傕偦偺悢偼恾-3偵帵偡傛偆偵丄晛捠偵掕婯偲僐儞僷僗傪巊偭偰嶌恾偱偒傞偺偱丄 柧傜偐偵楢懕検偺堦偮偲巚傢傟傞丅
3) 偵傕娭傢傜偢丄偦偺悢偵娭偟偰偼桳棟悢昞尰偑晄壜擻偱丄偟偐傕弞娐偟側偄柍尷彫悢偱昞偝傟傞偙偲偑傢偐偭偨丅
偦偟偰師偺偙偲偑埫栙偵壖掕偝傟傑偡丅
弞娐彫悢乮桳棟悢乯偲弞娐偟側偄柍尷彫悢乮柍棟悢乯偲偱丄楢懕検偼昞尰偝傟傞丅丂丂丂(7)
丂(7)偼杮摉偵惓偟偄偺偱偟傚偆偐丠丅(7)偑杮摉偵惓偟偄偐偳偆偐偼扤偵傕傢偐傝傑偣傫丅晛捠丄婥偵傕偝傟傑偣傫丅
婥偵傕偝傟側偄偲偼丄扤傕偙偺偙偲傪徹柧偟傛偆側偳偲偼婇偰側偄偙偲傪堄枴偟傑偡丅
偳偆偟偰偱偟傚偆丠丅彫悢偲偼桳棟悢昞尰傪僔僗僥儉壔偟偨傕偺丄偩偐傜偱偡丅
偦偟偰乽暔嵎偟 亖 桳棟悢 亖 楢懕検乿偲偄偆姶妎傪扤傕偑怣偠偰偄傞偐傜偩偲巚偊傑偡丅
偨偲偊彫悢昞尰偑旕弞娐偱偁偭偨偲偟偰傕丄尨揰偺傾僀僨傾偼扤傕偑惓偟偄偲姶偠傞偐傜偱偡丅
壖掕(7)偼幚嵺偺偲偙傠丄暔嵎偟偲偄偆尰幚偺暔懱乮暔棟揑尰幚乯偐傜敪憐偝傟偨暔棟揑壖掕偱偡丅
(7)偵懳偟偰悢妛揑媍榑傪峴偆偙偲偼偨傇傫晄壜擻側偺偱丄楢懕偺岞棟偲偱傕偄偆傋偒偦傟偼丄
悢妛彂偵梲側宍偱偼寛偟偰尰傟傑偣傫丅椺偊偽怷婤偼丄偦偺偁偨傝偺帠忣傪姰旛惈傪偐傜傔偰旕忢偵抁偔岅傝傑偟偨丅
偟偐偟崲偭偨帠懺偵側傝傑偟偨丅
俆丏壗偑崲傞偺偐丠
丂崲偭偨帠懺偲偼丄偙偆偄偆偙偲偱偡丅楢懕検偼丄弞娐彫悢偲旕弞娐彫悢偺慡懱偩偲掕媊偟偨応崌丄
弞娐彫悢偼桳棟悢偱丄偦偺峔惉朄傗寁嶼朄偑傢偐偭偰偄傑偡偑乮q亖m/n偩両乯丄
旕弞娐彫悢偵偮偄偰偼堦斒揑側峔惉婯懃偑傢偐傝傑偣傫丅旕弞娐彫悢偵偮偄偰傢偐偭偰偄傞偺偼丄
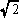 傗
傗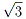 偲偐偺奐暯曽偵傛傞
摿庩側応崌偺峔惉婯懃偖傜偄偱偡丅偦偺懠慡偰偺旕弞娐彫悢偼丄偳偆傗偭偰掕媊偟偨傜椙偄偱偟傚偆丠丅
偲偙傠偑慺捈偵峫偊傞偲丄旕弞娐彫悢偺掕媊偼偡偱偵傢偐偭偰偄傞偺偱偼丠丄偲偄偆媈栤偑惗偠傑偡丅
幚嵺偙偆傗傟偽椙偄偲巚偊傑偡丅偄偭偨偄壗偑崲傞偺偐丠
偲偐偺奐暯曽偵傛傞
摿庩側応崌偺峔惉婯懃偖傜偄偱偡丅偦偺懠慡偰偺旕弞娐彫悢偼丄偳偆傗偭偰掕媊偟偨傜椙偄偱偟傚偆丠丅
偲偙傠偑慺捈偵峫偊傞偲丄旕弞娐彫悢偺掕媊偼偡偱偵傢偐偭偰偄傞偺偱偼丠丄偲偄偆媈栤偑惗偠傑偡丅
幚嵺偙偆傗傟偽椙偄偲巚偊傑偡丅偄偭偨偄壗偑崲傞偺偐丠

丂偙偺傛偆側姶妎偵廝傢傟傞偺偼丄変乆偵偲偭偰乵楢懕偺岞棟(7)乶偑旕忢偵嫮椡側岞棟偱丄 偨偲偊旕弞娐彫悢偺彫悢悢帤偺暲傋曽婯懃偑傢偐傜側偔偰傕丄偦傟偑偁傞偺偼妋偐側傫偩偐傜丄 暿偵偄偄偠傖側偄偐偲偄偆婥帩偪偵側傝傑偡丅偱偡偑(8)偺壓慄晹偵拲栚偡傞偲丄 弞娐偡傞応崌偼乽桳棟悢m/n乿偲偼偭偒傝偲偟偨梲側悢抣昞尰傪梌偊傜傟傑偡偑丄 弞娐偟側偄応崌偼乽偁傞柍棟悢乿偲偟偐偄偊傑偣傫丅偙偺堘偄偼廳梫偱偡丅 偮傑傝弞娐偟側偄柍尷彫悢傪尷傝側偔暲傋偰偄偭偨偲偒丄偦傟偑偁傞悢抣偵廂懇偡傞偙偲傪(8)偼曐徹偟偰偔傟傑偣傫丅 偙傟偼悢抣寁嶼忋偱傕廳梫側栤戣偱丄椺偊偽丄
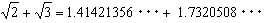 丂丂丂丂丂丂丂丂丂丂(9)
丂丂丂丂丂丂丂丂丂丂(9)
丂埲忋偺栤戣偼乵楢懕偺岞棟(7)乶偑曐徹偟偰偔傟傞偺偱偼丠丄偲巚偊傑偡偑丄(7)偼悢妛偺岞棟偱偼偁傝傑偣傫丅 傑偨(8)傗(9)偼尰幚偺栤戣偱丄(7)偑偄偐偵柧傜偐偵巚偊偰傕丄(8)傗(9)偺嬤帡寁嶼偑幚嵺偵廂懇偟側偗傟偽丄 (7)偼岆偭偨岞棟偩偲偄偆偙偲偵側傝傑偡丅旕弞娐彫悢偺廂懇惈偺曐徹偑昁梫偱偡丅 偦偙偼悢妛偑曐徹偟側偗傟偽側傝傑偣傫丅
俇丏僐乕僔乕楍
丂旕弞娐彫悢傪堦斒揑偵峔惉偡傞婯懃傪丄桳棟悢偺応崌傛偆偵巐懃墘嶼偵婎偯偄偰梌偊傞偙偲偼偱偒傑偣傫丅
偦偺尷奅偑傑偝偵桳棟悢偱偡丅壗屘巐懃墘嶼偱側偗傟偽側傜側偄偐偼乵楢懕偺岞棟(7)乶偺偨傔偱偡丅
堦斒婯懃側偺偱丄屄乆偺柍棟悢偼憡庤偵偱偒傑偣傫乮奐暯曽偵傛傞掕媊側偳乯丅
慡偰偺柍棟悢偵嫟捠偡傞惈幙傪庢傝弌偟偰丄梌偊曽傪掕媊偡傞昁梫偑偁傝傑偡丅
偝傜偵偦偺梌偊曽偼丄巐懃墘嶼偲惍崌偡傞昁梫傕偁傝傑偡丅
庤偑偐傝偼丄巐懃墘嶼偩偗傪巊偆幚悢偺彫悢揥奐朄偵偁傝傑偡丅
嵞傃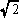 傪椺偵偲傝傑偡丅
傪椺偵偲傝傑偡丅
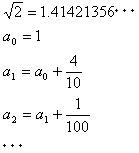 丂丂丂丂丂丂丂丂(10)
丂丂丂丂丂丂丂丂(10)
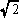 偼柍棟悢偱丄
悢楍(an)偺廂懇惈偵傛偭偰掕媊偟傛偆偲偟偨丄傑偝偵偦偺傕偺偱偡丅
偙傟偐傜掕媊偟傛偆偲偟偨傕偺偑丄掕媊偺拞偵昁梫偩偲偄偆帠懺偵側傝傑偡丅
惓妋偵偄偆偲丄桳棟悢楍(an)偑廂懇偡傞偺偼傎傏愨懳偵柧傜偐側偺偩偑丄
廂懇愭偑桳棟悢偱側偄偨傔偵枹掕媊忬懺偱偁傞丅
廂懇愭偑側偄偨傔偵丄廂懇偡傞悢楍偵懳偟偰廂懇偡傞偲尵偊側偄丅
壗屘側傜悢楍偺廂懇偼丄傆偮偆師偺傛偆偵掕媊偝傟傑偡丅
偼柍棟悢偱丄
悢楍(an)偺廂懇惈偵傛偭偰掕媊偟傛偆偲偟偨丄傑偝偵偦偺傕偺偱偡丅
偙傟偐傜掕媊偟傛偆偲偟偨傕偺偑丄掕媊偺拞偵昁梫偩偲偄偆帠懺偵側傝傑偡丅
惓妋偵偄偆偲丄桳棟悢楍(an)偑廂懇偡傞偺偼傎傏愨懳偵柧傜偐側偺偩偑丄
廂懇愭偑桳棟悢偱側偄偨傔偵枹掕媊忬懺偱偁傞丅
廂懇愭偑側偄偨傔偵丄廂懇偡傞悢楍偵懳偟偰廂懇偡傞偲尵偊側偄丅
壗屘側傜悢楍偺廂懇偼丄傆偮偆師偺傛偆偵掕媊偝傟傑偡丅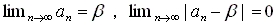 丂丂丂丂丂丂丂丂(11)
丂丂丂丂丂丂丂丂(11)
兠伕俼偲偟偰丄偁傞兝伕俼偑懚嵼偟丄偲側傝傑偡丅廂懇敾掕偵偼(11)傗(12)偺傛偆偵丄廂懇愭兝偑搊応偟傑偡丅 偟偐偟(7)偺彆偗傪庁傝偨偵偟偰傕丄(10)偑廂懇偡傞偙偲偼柧傜偐偱偡丅 偟偐傕
擟堄偺兠亜0偵懳偟偰n0伕俶偑偦傟偧傟掕傑偭偰丄n0亙値側傜|an亅兝|亙兠丂丂丂丂丂丂 (12)
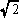 偺柍尷彫悢揥奐傪嵟屻傑偱幚峴偟偨恖偼扤傕偄側偄偲偄偆偺偵偱偡
乮柍尷偺掕媊(6)乯丅
廂懇寢壥偼扤傕尒偨偙偲偑側偄偺偵丄廂懇偡傞偲妋怣偱偒傑偡丅
廂懇寢壥傪巊傢側偄偱丄悢楍偺廂懇傪敾掕偡傞曽朄偑偁傞偼偢偱偡丅僐乕僔乕楍偼埲壓偺傛偆偵掕媊偝傟傑偡丅
偺柍尷彫悢揥奐傪嵟屻傑偱幚峴偟偨恖偼扤傕偄側偄偲偄偆偺偵偱偡
乮柍尷偺掕媊(6)乯丅
廂懇寢壥偼扤傕尒偨偙偲偑側偄偺偵丄廂懇偡傞偲妋怣偱偒傑偡丅
廂懇寢壥傪巊傢側偄偱丄悢楍偺廂懇傪敾掕偡傞曽朄偑偁傞偼偢偱偡丅僐乕僔乕楍偼埲壓偺傛偆偵掕媊偝傟傑偡丅掕媊侾乮僐乕僔乕楍乯
兠伕俼偲偟偰丄擟堄偺兠亜0偵懳偟偰n0伕俶偑偁傝丄n0亙値丆倣 側傜|an亅am|亙兠丏偲側傞悢楍(an)n伕俶 傪丄僐乕僔乕楍偲偄偆丅偄偄偐偊傟偽丄
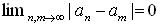
丂掕媊侾偺兠伕俼傪兠伕俻乮俻偼桳棟悢慡懱乯偵偍偒偐偊傟偽丄俻傑偱偼掕媊偱偒偨偲偄偆尰嵼偺忬嫷偱丄 僐乕僔乕楍傪廂懇敾掕偵巊偊傑偡丅廂懇楍偑僐乕僔乕楍偱偁傞偙偲偼丄娙扨偵徹柧偱偒傑偡丅
掕棟3
廂懇楍偼丄僐乕僔乕楍丅
乵徹柧乶
丂丂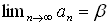
偲偡傞丅晄摍幃丄
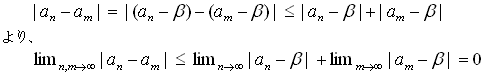
偲側傞丅丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乵徹柧廔傢傝乶
丂媡偼偳偆偱偟傚偆丠丅擟堄偺幚悢偺彫悢揥奐偑僐乕僔乕楍偱偁傞偙偲偼丄偡偖傢偐傝傑偡乮椺偊偽(10)乯丅
乽僐乕僔乕楍偼廂懇楍乿偑尵偊傟偽丄桳棟悢偺僐乕僔乕楍傪傕偭偰柍尷彫悢揥奐偺廂懇惈傪曐徹偱偒偦偆偱偡丅
偨偩偟傑偩廂懇愭偼枹掕媊忬懺偱偡偑丄杮幙偼掕媊侾偱恠偔偝傟偰偄傞傛偆偵巚偊傑偡丅
偦偺妋怣偼(10)偵傛偆側幚嵺偺寁嶼宱尡偵桼棃偟傑偡丅
偦偙偱乵楢懕偺岞棟(7)乶偵傛偭偰奣擮揑偵偼掕媊偝傟偨幚悢慡懱俼偑丄偡偱偵偁傞傕偺偲壖掕偟傑偡丅
偙偺壖掕傪庴偗擖傟傞偲媡傪徹柧偱偒傑偡丅
庴尡悢妛偺巹揑揝懃偲偟偰丄偁傞梊旛峑偺悢妛島巘偑偙偆尵偭偰偄偨偺傪巚偄弌偟傑偡丅
乽悢妛偱偼丄搒崌偺椙偄偙偲傪愭偵憐掕偟偰偦偙偵岦偐偭偰寁嶼偡傞偲丄偗偭偙偆偆傑偔偄偔丒丒丒乿丂栤戣夝寛偺曽朄榑偲偟偰丄傾僂僩儔僀儞傪愭偵尒捠偟偰曽恓傪棫偰傛丄偲偄偆偙偲偱偟傚偆偑丄 偙偺敪憐偑寢嬊偼姰旛壔偺奣擮偵偮側偑傝傑偡丅僾儘僌儔儉偺悽奅偺傾僾儕働乕僔儑儞愝寁偱傕丄 僩僢僾僟僂儞曽幃偼桳岠偱偡丅偲偄偆傢偗偱丄偦傟偼偁傞偼偢偩偐傜丄 幚悢偺廤崌俼偼偡偱偵懚嵼偡傞偲壖掕偟傑偡丅
掕棟4
幚悢偼掕媊偝傟偨偲壖掕偡傞丅僐乕僔乕楍偼廂懇楍丅
乵徹柧乶
丂傆偮偆丄偙偺徹柧偼傎偲傫偳柍帇偝傟傑偡丅屻弎偟傑偡偑丄幚悢偑掕媊偝傟廔傢偭偨忬懺偱偼丄
偙偺帠幚偼柧傜偐偩偐傜偱偡丅偦傟偼桳棟悢傪姰旛壔偟偰幚悢傪掕媊偡傞偲偄偆峔惉朄偦偺傕偺偐傜棃偰偄偰丄
偙傟偑幚悢榑偺傢偐傝偵偔偝偺堦偮偵側偭偰偄傞偲巚偄傑偡丅
偙偙偱偼幚嵺偵僐乕僔乕楍偑廂懇楍偵側傞偙偲傪尒偨偄偺偱丄儀僞側徹柧傪帋傒傑偡丅
丂堦斒偵悢楍偺廂懇惈傪埖偆応崌丄偦傟偼杮棃摓払偱偒側偄柍尷偺斵曽偺寢壥傪弌偦偆偲偡傞偙偲偱偡丅
掕棟3偺傛偆偵丄偁偭偝傝曅晅偔応崌傕偁傝傑偡偑丄婎杮偼乽柍尷偺掕媊(6)乿偱偡丅(6)偼師偺傛偆偵尵偭偰偄傑偡丅
乽柍尷偺斵曽傪徹柧偟偨偄側傜丄攚棟朄偵傛偭偰桳尷懁偐傜峌傔傠丅偦傟偑偱偒傞偙偲慡偰偩乿偲丅
丂僐乕僔乕楍 (an)n伕俶偑廂懇楍偱側偄偲壖掕偡傞丅廂懇楍偱側偄偲偼丄(12)傪嵞婰偟偨(13)偺斲掕偲摨偠丅
兠伕俼偲偟偰丄偁傞兝伕俼偑懚嵼偟丄偺斲掕偼乮兠伕俼偼丄撉傒偵偔偄偺偱徣棯偡傞乯丄
擟堄偺兠亜0偵懳偟偰n0伕俶偑偦傟偧傟掕傑偭偰丄n0亙値側傜|an亅兝|亙兠丂丂丂丂丂 (13)
擟堄偺兝伕俼偵偮偄偰丄偁傞兠亜0偑偦傟偧傟掕傑傝丄偦偺兠偵懳偟偰偼丄偲側傞丅(14)偼妋偐偵 (an)偑廂懇偱偒側偄堄枴偵側傞丅偙偙偱兝偼擟堄側偺偱丄兝亖am偲偍偗偽丄
偳傫側n伕俶傪帩偭偰偒偰傕丄|an亅兝|亞兠 偑惉棫偮丂丂丂丂丂丂丂丂丂丂丂丂丂 (14)
偳傫側n丆m伕俶偵偮偄偰傕丄偁傞兠亜0偑偦傟偧傟掕傑傝丄偲側傞偑丄偙傟偼掕媊侾偺斲掕偱偁傞丅傛偭偰僐乕僔乕楍 (an)偼丄僐乕僔乕楍偱側偄丅 偙傟偼柕弬丅廬偭偰丄僐乕僔乕楍 (an)n伕俶 偼廂懇楍丅
偦偺兠偵懳偟偰偼丄|an亅am|亞兠 偱偁傞丂丂丂丂丂丂丂丂丂丂丂丂丂丂 (15)
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乵徹柧廔傢傝乶
俈丏僐乕僔乕楍偺摨抣椶
丂偙偙傑偱偱偗偭偙偆挿偔側偭偰偟傑偄傑偟偨偑丄偙偺摨抣椶偝偊曅晅偗傟偽丄幚悢偺峔惉偼傎傏姰惉偱偡丅
偁偲偼乽姰旛壔両乿偲嫨傇偩偗偱帠偼廔傢傝傑偡丅慜愡傑偱偱丄僐乕僔乕楍偲廂懇楍偼杮幙揑偵摨偠偱丄
僐乕僔乕楍偱傕偭偰擟堄偺幚悢傪掕媊偱偒偦偆側偙偲偑傢偐傝傑偟偨偑丄傑偩栤戣偑偁傝傑偡丅
偦傟偼丄偁傞幚悢傪掕媊偡傞僐乕僔乕楍偼桞堦偮偱偼側偄丄偲偄偆帠幚偱偡丅
椺偊偽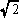 偺彫悢揥奐(10)偵偍偄偰尰傟偨僐乕僔乕楍(an)偺晹暘楍偼丄
傗偼傝
偺彫悢揥奐(10)偵偍偄偰尰傟偨僐乕僔乕楍(an)偺晹暘楍偼丄
傗偼傝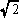 偵廂懇偟傑偡丅
晹暘楍偺偲傝曽偼柍悢偵偁傝傑偡丅傑偨尰幚揑側悢抣寁嶼傪峫偊偨応崌丄幚嵺栤戣偦傟偼丄
偄偔偮偐偺僐乕僔乕楍偺娫偺墘嶼偵側傝傑偡丅2偮偺僐乕僔乕楍(an)丆(bn)傪峫偊偨偲偒丄
偦傟傜偑摨偠幚悢傪掕媊偡傞偺偐丄偦偆偱側偄偺偐偔傜偄傪敾掕偱偒側偄偲丄悢抣寁嶼偡傜偱偒傑偣傫丅
(an)亄(bn)亖(cn)偲偍偄偨応崌丄(cn)亖(an亄bn)偱椙偄偺偐丠偲偄偆榖偱偡丅
偙傫側偺摉偨傝慜偱偼側偄偐偲巚偊傑偡偑丄(cn)偺廂懇愭偵廂懇偡傞偺偼丄(an亄bn)偩偗偱偼偁傝傑偣傫丅
堦偮偺幚悢傪嬤帡偡傞曽朄偼柍悢偵偁傝丄偦偺偦傟偧傟偑僐乕僔乕楍傪惗傒弌偟傑偡丅
偳傫側嬤帡曽朄傪偲偭偰傕乮偳傫側僐乕僔乕楍傪巊偭偰傕乯丄偦傟偑摍壙側嬤帡偱偁傞側傜偽丄
忢偵摨偠廂懇愭傪帩偮偙偲傪曐徹偟側偗傟偽側傝傑偣傫丅偟偐傕尰嵼偼傑偩丄幚悢傪掕媊偡傞埲慜偺忬懺偱偡丅
師偺傛偆側徹柧偼偱偒側偄傢偗偱偡丅
偵廂懇偟傑偡丅
晹暘楍偺偲傝曽偼柍悢偵偁傝傑偡丅傑偨尰幚揑側悢抣寁嶼傪峫偊偨応崌丄幚嵺栤戣偦傟偼丄
偄偔偮偐偺僐乕僔乕楍偺娫偺墘嶼偵側傝傑偡丅2偮偺僐乕僔乕楍(an)丆(bn)傪峫偊偨偲偒丄
偦傟傜偑摨偠幚悢傪掕媊偡傞偺偐丄偦偆偱側偄偺偐偔傜偄傪敾掕偱偒側偄偲丄悢抣寁嶼偡傜偱偒傑偣傫丅
(an)亄(bn)亖(cn)偲偍偄偨応崌丄(cn)亖(an亄bn)偱椙偄偺偐丠偲偄偆榖偱偡丅
偙傫側偺摉偨傝慜偱偼側偄偐偲巚偊傑偡偑丄(cn)偺廂懇愭偵廂懇偡傞偺偼丄(an亄bn)偩偗偱偼偁傝傑偣傫丅
堦偮偺幚悢傪嬤帡偡傞曽朄偼柍悢偵偁傝丄偦偺偦傟偧傟偑僐乕僔乕楍傪惗傒弌偟傑偡丅
偳傫側嬤帡曽朄傪偲偭偰傕乮偳傫側僐乕僔乕楍傪巊偭偰傕乯丄偦傟偑摍壙側嬤帡偱偁傞側傜偽丄
忢偵摨偠廂懇愭傪帩偮偙偲傪曐徹偟側偗傟偽側傝傑偣傫丅偟偐傕尰嵼偼傑偩丄幚悢傪掕媊偡傞埲慜偺忬懺偱偡丅
師偺傛偆側徹柧偼偱偒側偄傢偗偱偡丅
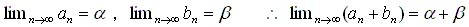
掕媊2乮摨抣側僐乕僔乕楍乯
丂(an)偲(bn)傪僐乕僔乕楍偲偡傞丅
兠伕俼偲偟偰丄擟堄偺兠亜0偵懳偟偰n0伕俶偑偁傝丄 n0亙値丆倣 側傜|an亅bm|亙兠丏偲側傞偲偒丄悢楍 (an)n伕俶 偲(bn)n伕俶 偼摨抣側僐乕僔乕楍偱偁傞偲偄偆丅 偙傟傪丄(an)佭(bn)丗mode C 偱昞偡丅 偄偄偐偊傟偽丄(an)偲(bn)傪僐乕僔乕楍偲偟偨偲偒丄
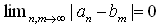
丂尰嵼偼傑偩幚悢傪掕媊偡傞埲慜側偺偱丄兠伕俼偼兠伕俻偵撉傒懼偊偰偔偩偝偄丅 師偺掕棟偼傎傏柧傜偐偱偡偑丄慜偲摨偠棟桼偱傆偮偆柍帇偝傟傞偺偱丄傗偭偰偍偒傑偡丅
掕棟5
丂幚悢偼掕媊偝傟偨偲壖掕偡傞丅摨抣側僐乕僔乕楍偼摨偠抣偵廂懇偡傞丅
乵徹柧乶
丂(an)偲(bn)傪摨抣側僐乕僔乕楍偲偡傞丅
僐乕僔乕楍偼廂懇楍側偺偱丄
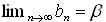 偑懚嵼偡傞丅偙傟偼丄
偑懚嵼偡傞丅偙傟偼丄
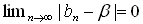
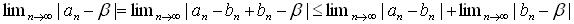
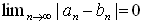
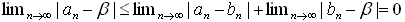
摨抣側僐乕僔乕楍偼丄摨抣椶傪偮偔傝傑偡丅摨抣娭學傪棙梡偡傞傢偗偼丄偡偖屻偵弎傋傑偡丅
掕棟6
摨抣側僐乕僔乕楍偼丄摨抣娭學偵偁傞丅
乵徹柧乶
1) 斀幩惈
僐乕僔乕楍偺掕媊傛傝丄 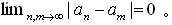
(an)佭(an)丗mode C 偑惉棫偮丅
2) 懳徧惈
丂丂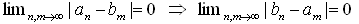
偼柧傜偐丅
(an)佭(bn)丗mode C 佀 (bn)佭(an)丗mode C 偑惉棫偮丅
3) 悇堏惈
丂丂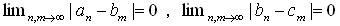
側傜丄
丂丂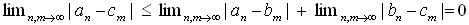
偲側傞丅
(an)佭(bn)丗mode C 偐偮 (bn)佭(cn)丗mode C 佀 (an)佭(cn)丗mode C 偑惉棫偮丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乵徹柧廔傢傝乶
丂mode C偼掕棟6偺1)乣3)偺惈幙傪枮偨偟傑偡丅
惈幙1)乣3)傪枮偨偡娭學偱寢偽傟偨懳徾慡懱偺廤崌偺偙偲傪丄摨抣椶偲偄偆偺偼偛懚抦偲巚偄傑偡偑丄
摨抣椶偺堦偮偺梫慺乮戙昞尦偲偄偄傑偡乯偵偮偄偰惉棫偮惈幙偼丄摨偠摨抣椶偵懏偡傞慡偰偺梫慺偵懳偟偰惉棫偟傑偡丅
偦傟傪曐徹偡傞偺偑1)乣3)偱偡丅
崱偺応崌丄偦偺娭學偼mode C乮摨抣側僐乕僔乕楍乯偲偄偆傕偺偱丄
mode C偺娭學偵偁傞2偮偺僐乕僔乕楍偼掕棟5傛傝摨偠廂懇愭傪帩偮偨傔丄
摨偠摨抣椶偵懏偡傞慡偰偺僐乕僔乕楍偼堦偮偺幚悢傪掕媊偡傞丄偲偄偆傢偗偱偡丅
偙傟偵傛偭偰丄摨抣椶偵娷傑傟傞堦偮偺僐乕僔乕楍偵懳偟偰偁傞悢抣寁嶼傪妋擣偟偝偊偡傟偽丄
偦偺懠偺慡偰偺摨抣側僐乕僔乕楍傪巊梡偟偰傕摨偠寢壥偵側傞偙偲偑曐徹偝傟傑偡丅
偙偙傑偱傗偭偰弶傔偰丄摍壙側嬤帡偲偄偆奣擮傪惓妋偵昞尰偱偒偨偙偲偵傕側傝傑偡丅
偟偐偟傑偩愭偑偁傝傑偡丅
掕媊3乮幚悢偺掕媊乯
桳棟悢俻偐傜惗惉偝傟傞摨抣側僐乕僔乕楍偺摨抣椶慡懱偺偙偲傪丄幚悢偲偄偄俼偱昞偡丅俻伡俼偼柧傜偐丅
掕媊3偑乽姰旛壔両乿偺嫨傃偱偡丅
俉丏廤崌榑搊応両乮懄暔惈偲嬶懱惈偺嬌傒乯
掕媊3偼偄偭偨偄壗傪偄偭偰傞偺偱偟傚偆丠丅
傑偢俻伡俼側偺偼丄俻偐傜惗惉偝傟傞僐乕僔乕楍偺拞偵偼丄桳棟悢偵廂懇偡傞傕偺傕丄傕偪傠傫娷傑傟傞偐傜偱偡丅
偦偺傛偆側僐乕僔乕楍偺摨抣椶1偮1偮偼丄傆偮偆偵峫偊偨桳棟悢偺1屄1屄偲丄1懳1偵懳墳偟偰懳墳楻傟傕偁傝傑偣傫丅
傑偨偙偙偱偼徣棯偟傑偡偑丄(an)偲(bn)傪僐乕僔乕楍偲偟偨偲偒丄
(an)亄(bn)亖(an亄bn)偲偟偰椙偄偙偲偑徹柧偱偒傑偡丅
摨條側娭學幃偑巐懃墘嶼慡偰偱惉傝棫偪傑偡丅偦偟偰偙偺惈幙偼摨偠摨抣椶偵娷傑傟傞慡偰偺僐乕僔乕楍偱傕惉棫偟傑偡丅
偙偙偐傜丄兛偲兝偑桳棟悢偱偁傝丄偦傟傜偑僐乕僔乕楍(an)偲(bn)偺廂懇愭側傜偽丄偦偺摨抣椶傪俙丆俛偲偟偰丄
丂僐乕僔乕楍傪帩偪弌偟偨傕偲傕偲偺棟桼偼丄堦斒揑側柍棟悢偺梌偊曽偑丄尰幚栤戣偲偟偰柍尷彫悢揥奐傪 棙梡偡傞偟偐庤偑側偐偭偨偐傜偱偡丅偱偼偙偺尰幚栤戣偼丄夝寛壜擻偱偟傚偆偐丠丅 乽偦傟偼偱偒側偄乿偲偄偆攕杒愰尵偑掕媊3偱偡丅柍尷偺僷僞乕儞偑偁傝丄柍尷偵寘悢偑憹偊偰偄偔彫悢揥奐偵懳偟偰丄 尵梩偵傛傞峔惉揑婯懃晅偗偼偱偒側偐偭偨偲尵偭偰傕摨偠偱偡丅偙傟偼柍尷偵懳偡傞攕杒愰尵偱傕偁傝傑偡丅 偦偺崻偼傗偼傝丄柍尷偺掕媊(6)偱偡丅偙偙偱廤崌榑偑搊応偟傑偡丅
乮掕媊3偵傛偆偵丄廤傑偭偨偲巚偊偽椙偄両乯
丂廤傔偨偐傜壗偩偭偰偄偆傫偱偟傚偆丠丅廤崌榑偵偼丄師偺傛偆側巚憐偑捠掅偟偰偄傞偲巚偄傑偡丅
丂崱偺応崌偵偼丄偙偆側傝傑偡丅僐乕僔乕楍傪帩偪弌偟偨傕偲傕偲偺棟桼偼丄
柍尷彫悢揥奐傪棙梡偡傞偟偐庤偑側偐偭偨偐傜偱偡丅(6)傛傝丄傕偟偙傟偟偐庤偑側偄偺偱偁傟偽丄
偁傞僐乕僔乕楍偑掕媊偡傞摨抣椶偵偼丄変乆偑柍棟悢偵娭偟偰峴偊傞慡偰偺峴堊偺寢壥偑娷傑傟偰偄傑偡丅
変乆偑偁傞柍棟悢偵偮偄偰丄桳尷憖嶌偱抦傝偊傞慡偰偺忣曬偑偦偙偵偼媗傑偭偰偄傑偡丅
偦偟偰丄偦傟傪傕偲偵偟偰柍棟悢傪掕媊偟偨偺偱偟偨丅
変乆偺偱偒傞偙偲偼丄偦傟偱慡偰偩丅丂丂丂(17)
偨傇傫偙傟偑丄掕媊3偺杮摉偺堄枴偱偡丅廤崌榑偼拪徾揑偩偲巚傢傟偑偪偱偡偑丄斀柺偙偺傛偆偵丄
寵偵側傞偔傜偄偺懄暔惈偲嬶懱惈偺尃壔偱偡丅
丂偙偺傛偆側孹岦偼僸儖儀儖僩偺宍幃庡媊埲棃丄僽儖僶僉偵傛傞峔憿庡媊傪宱偰丄妋幚偵掕拝偟偨偲巚偄傑偡丅
宍幃庡媊傗峔憿庡媊偵偍偄偰丄幚悢傗柍棟悢側偳偺懳徾暔偼柍掕媊梫慺偲傒側偝傟傑偡丅
柍掕媊梫慺娫偺娭學傪惓妋偵掕媊偡傞偙偲偵傛傝丄娭學偑媡偵柍掕媊梫慺偵堄枴傪晅梌偡傞偲偄偆偺偑丄
峔憿庡媊偺棫応偱偡丅偟偐傕堄枴傪媯傒庢傞偐偳偆偐偼丄偁傞棟榑傪撉傫偩恖偺彑庤偲偄偆偙偲偵側偭偰偄傑偡丅
悢妛棟榑偑偁傞巚憐傗堄枴偵婎偯偄偰棫偰傜傟傞偺偼妋偐偩偲巚偄傑偡偑丄掕幃壔偼偦偆偱側偄偲偄偆偙偲偱偡丅
偙偺棫応偼弶妛幰偵懳偟偰丄夁戝側孭楙傪梫媮偟傑偡丅偳偆偟偰偐偲偄偆偲丄柍掕媊梫慺偱彂偐傟偨岞棟傪変枬偟偰
撉傫偱乮偍傏偊偰乯丄棟榑慡懱傪偁傞掱搙棟夝偟尒搉偟偨屻偱丄弶傔偰堄枴偑傢偐傞偐傜偱偡丅
偦偺忋丄堄枴傪媯傒庢傞偐偳偆偐偵偮偄偰偼撉傫偩恖偺彑庤側偺偱偡偐傜丄弶妛幰偺夝庍偼娫堘偄偐傕偟傟傑偣傫丅
弶傔偰幚悢榑傪撉傫偩恖偑丄乽柧夣側夝摎偑梡堄偝傟偰偄偨乿側偳偲巚偆傢偗偑偁傝傑偣傫丅
俋丏嵞傃乽姰旛壔両乿
丂偱偼榑棟揑側弴彉偵廬偭偨幚悢偺峔惉傪弎傋傑偡丅
巜愜傝嶼乮悢偵傛偆側傕偺丅斖埻偼桳尷乯佀 帺慠悢俶 佀 惍悢倅 佀 桳棟悢俻 佀 幚悢俼
嘆偺惗惉尨棟丗 壛朄偵傛傞儁傾僲岞棟宯丅壛朄偺徣棯婰朄偲偟偰忔朄傪摫擖丅
嘇偺惗惉尨棟丗 壛朄偺媡墘嶼尭朄丅尭朄偵懳偡傞俶偺戙悢揑懳徧壔丅
嘊偺惗惉尨棟丗 忔朄偺媡墘嶼彍朄丅彍朄偵懳偡傞倅偺戙悢揑懳徧壔丅
嘋偺惗惉尨棟丗 俻偺姰旛壔丅俻偺僐乕僔乕楍偺摨抣椶慡懱偺堦晹偲偟偰丄俻傪摨抣椶慡懱偺晹暘廤崌偲摨堦帇偟丄
俻偲僐乕僔乕楍偺摨抣椶慡懱偺崌暪傪偲傞丅
丂掕棟4偲5偑傆偮偆柍帇偝傟傞棟桼偼丄惗惉尨棟嘋偱偡丅僐乕僔乕楍偼廂懇楍偱偟偨偑丄
廂懇愭偑俻偺拞偵側偄偨傔偵丄偦傟傪廂懇楍偲偼屇傋傑偣傫偱偟偨丅偲偙傠偑僐乕僔乕楍偼杮幙揑偵偼廂懇楍側偺偱丄
偦傟帺懱傪廂懇愭偲摨堦帇偟丄偦傟傪慡偰俻偵揧壛偡傞偲偄偆偺偑嘋偱偡丅廂懇偟偰梸偟偄傕偺傪廂懇寢壥偲摨偠偩
傒側偟偰揧壛偡傞偺偱偡偐傜丄幚悢俼偺拞偱僐乕僔乕楍偑廂懇偡傞偺偼摉慠偱偡乮掕棟4乯丅
傑偨僐乕僔乕楍偼廂懇楍側偺偱丄摨抣側僐乕僔乕楍偑摨偠幚悢偵廂懇偡傞偺傕摉慠偱偡乮掕棟5乯丅
姰旛壔偺惓幃側掕媊偼丄埲壓偺傛偆偵側傝傑偡丅
掕媊4乮姰旛壔乯
丂擟堄偺僐乕僔乕楍偑廂懇偱偒傞傛偆偵偡傞偙偲傪丄姰旛壔偲偄偆丅
丂怷婤偼乽姰旛壔偡傟偽僐乕僔乕楍偑昁偢廂懇偡傞偙偲乿偵偮偄偰丄乽偦偆偄偆晽偵憿偭偨傫偩偐傜丄
偦傫側偺摉偨傝慜偩傠偆両乿偲搟傝傑偟偨丅偦偟偰乽幚悢棟榑偼丄悢妛揑偵偼惓摉偩偑搒崌偺椙偄僼傿僋僔儑儞偩乿
偲尵偄愗傝傑偡丅巹偼偙傟傪乵楢懕偺岞棟(7)乶偺偙偲傪尵偭偰偄傞傕偺偲丄彑庤偵夝庍偟偰偄傑偡丅
丂惗惉尨棟嘆乣嘊偵偼丄幚悢偺傾僀僨傾偺尨揰乽暔嵎偟 亖 桳棟悢 亖 楢懕検乿偑柧妋偵摥偄偰偄傞偲巚偄傑偡丅
嘊偐傜嘋傊偺堏峴偵偼丄偦偺墑挿慄忋偵偁傞(7)偑昁梫偱偡丅偦傟傪擣傔偨忋偱丄偦偆偡傞偟偐側偐偭偨偙偲傪柧妋
偵擣傔偨偺偑(17)偲巚偊傑偡丅乵楢懕偺岞棟(7)乶偼悢妛偺岞棟偱偼偁傝傑偣傫丅尰嵼偺偲偙傠扤傕徹柧偱偒偰偄傑偣傫丅
偡傞昁梫偑偁傞偺偐丠偲偄偆媍榑傕娷傔偰偦偆巚偄傑偡丅悢妛婎慴榑偲偼丄偒偭偲偙偆偄偆榖傪傗偭偰偔傟傞
暘栰偵堘偄側偄偲丄彑庤偵巚偭偰偄偨帪婜偑偁傝傑偟偨丅
丂幚悢偺峔惉偼嵟屻偺嵟屻傑偱丄乽暔嵎偟 亖 桳棟悢 亖 楢懕検乿偺傾僀僨傾偺墑挿慄忋偵偁傝傑偡丅
幚悢奣擮偵懳偡傞尨揰偺傾僀僨傾偼丄傎偲傫偳偦偺傑傑惓偟偐偭偨偺偩偲巚偄傑偡丅
偨偩巚傢偸張偱柍尷戝偵弌夛偭偰偟傑偭偨偲偄偆丄偨偩偦傟偩偗偺帠偱偡丅偦偆偄偆堄枴偵偍偄偰丄
僐乕僔乕楍傗偦偺摨抣椶偼悢妛揑偵偼昁梫偱揔惓側摴嬶棫偰偱偡偑丄尨揰偺傾僀僨傾偺晄旛傪曗偆柺搢側曗彆媍榑偩偭
偨偲偡傞偺偼丄傗偼傝尵偄夁偓偱偟傚偆偐丠丅
10丏嵟屻偵懳妏慄榑朄
丂偙偙偱偄偆懳妏慄榑朄偲偼丄幚悢偺屄悢偑桳棟悢傛傝懡偄偙偲傪帵偡抂揑側徹柧偺偙偲偱偡丅
廤崌俙偺梫慺偺屄悢傪 Card(俙)偱昞偟傑偡丅
偑惉棫偪傑偡丅Card(俶)偼壜嶼柍尷偲偄傢傟丄俶偺掕媊偐傜柧傜偐側傛偆偵丄擟堄桳尷慡偰傪廤傔偨柍尷偱偡丅 梫慺偼慡晹桳尷側偺偵丄壗屘偦偺廤崌偼柍尷偵側傞偺丠偲巚傢傟傞曽偼丄変揷堷悈偱偡偑NO.1476傪偛棗偔偩偝偄丅 巹偵傢偐傞尷傝偼丄偦偙偱愢柧偟傑偟偨丅壜嶼柍尷偼傑偨丄柍尷偺庻柦傪帩偭偨恖娫偑偄偨偲偟偰丄 偺恖偑摓払偱偒傞嵟戝偺柍尷偱偡丅偙傟偼丄恖娫偑摓払偱偒傞偐傕偟傟側偄孞傝曉偟夞悢偺嵟戝偱偁傞偲尵偄偐偊偰傕 摨偠偱偡丅俶偐傜俻傊偺悢偺奼挘偼丄惗惉尨棟嘆乣嘊偵懳墳偟偰慡偰戙悢揑側傕偺偱偡丅 戙悢憖嶌偺孞傝曉偟夞悢偼桳尷偑婎杮側偺偱丄偦偺慡懱偼丄恖娫偑摓払偱偒傞偐傕偟傟側偄孞傝曉偟夞悢偺 嵟戝偱偁傞壜嶼柍尷偵摍偟偔側傝傑偡丅 偦偆峫偊傞偲丄壜嶼柍尷側俶偐傜壜嶼柍尷側戙悢揑奼挘偱摓払偟偨俻傕傗偼傝壜嶼柍尷偱丄 Card(俶)亖Card(俻)側偺偼偁傞堄枴摉慠側偺偐傕偟傟傑偣傫乮嵟弶偼娞傪偮傇偟傑偡偑乯丅 梫偡傞偵俶偐傜俻傊偺奼挘偵偼丄嬌尷憖嶌偑娷傑傟偰偄側偄偲偄偆偙偲偱偡丅 俻偐傜俼傊偺奼挘偵偼丄僐乕僔乕楍偲偄偆嬌尷憖嶌偑婎慴偵側傝傑偡丅 偙偺嬌尷憖嶌偺寢壥偑丄偄偐偵戝偒側柍尷戝傪惗傒弌偡偐傪帵偡偺偑丄僇儞僩儖偺懳妏慄榑朄偱偡丅 徹柧帺懱偼偁偭偗側偄偔傜偄娙扨偱偡偑丄傑偨傕攚棟朄偱偡丅
掕棟7乮懳妏慄榑朄乯
丂丂丂丂Card(俶)亙Card(俼)丅
乵徹柧乶
丂俼慡懱偱偼埖偄偵偔偄偺偱丄嬫娫俬亖[0丆1]傪椺偵偲傞丅Card(俬)亝Card(俼)偼柧傜偐丅
Card(俶)亖Card(俬)偑惉傝棫偮偐偳偆偐偺敾掕傪峴偆丅
偦傟偵偼丄俬偺梫慺1屄1屄傪丄俶偺梫慺偱偁傞0丆1丆2丆丒丒丒偱斣崋晅偗偟偰偄偗偽椙偄丅
斣崋楻傟偑側偗傟偽Card(俶)亖Card(俬)丅
丂俬偺梫慺傪彫悢揥奐偟斣崋晅偗偟偨偲偙傠丄斣崋晅偗偵惉岟偟偨偲壖掕偡傞丅偦傟傪憐憸偡傞偲壓恾丅
丂丂
偨偩偟aij偼悢帤0乣9偺偳傟偐丅偲偙傠偑師偺傛偆側幚悢兛傪峔惉偱偒傞丅
兛亖0.b1 b2 b3 b4 丒丒丒
偙偙偱丄bi偼恾-4偺aii偲昁偢堘偆悢偲偡傞丅
偦偆偡傞偲兛偺彫悢埲壓倝寘栚bi偼丄恾-4偺俬偺梫慺偺懳妏慄a11丆a22丆a33丆丒丒丒偲昁偢堎側傞偐傜丄
兛偼恾-4偵昞傟傞偳偺俬偺梫慺偲傕摍偟偔側偄丅偐偮0亝兛亝1偼柧傜偐偩偐傜丄兛伕俬偱傕偁傞丅
偡側傢偪Card(俶)亖Card(俬)偲偟偰斣崋晅偗偵惉岟偟偨偲壖掕偟偨傜丄斣崋楻傟偑偁偭偨丅偙傟偼柕弬丅
傛偭偰丄Card(俶)亙Card(俬)亝Card(俼)丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乵徹柧廔傢傝乶
丂Card(俶)亖Card(俻)偩偭偨偺偱丄偙傟偼桳棟悢慡懱偺悢傪傕偭偰偟偰傕Card(俼)偵偼媦偽側偄偙偲傪堄枴偟傑偡丅
Card(俼)偼楢懕柍尷偲屇偽傟傑偡偑丄偙偺柍尷偼壜嶼柍尷傛傝偳傟偔傜偄戝偒偄偺偱偟傚偆丠丅
乽柍尷偺掕媊(6)乿傪巚偄弌偟偰傒傑偡丅偦傟偼丄
偲偄偆傕偺偱偟偨丅偦偺偨傔偵柍尷偵娭傢傞徹柧傪峴偆応崌偵偼攚棟朄偑杮幙揑庤朄偲側傝丄 攚棟朄偵傛偭偰柍尷傪桳尷懁偵堷偒栠偟偰徹柧偡傞偟偐側偄帠懺偲側傝傑偡丅懳妏慄榑朄傕攚棟朄偱偡丅 攚棟朄偵傛偭偰楢懕柍尷傪壜嶼柍尷懁偵堷偒栠偟偰徹柧偟偰偄傑偡丅崱偺応崌偵(6)偵憡摉偡傞傕偺傪憐憸偡傞偲丄
偲側傝偦偆偱偡丅(6)偱掕媊偝傟偨柍尷偵懳偟偰丄慡偰偺擟堄桳尷偼僇僗偵摍偟偄偔傜偄彫偝側傕偺偱偡丅 偲偄偆偙偲偼丄楢懕柍尷偼壜嶼柍尷偑僇僗偵尒偊傞偔傜偄戝偒側傕偺偱偁傞偙偲偑憐憸偱偒傑偡丅 掕媊3偺偨偭偨偺堦暥偵旕峔惉揑偵娷傑傟偰偄偨嬌尷憖嶌偼丄挻嫄戝偱偡丅 偦傟偼柍尷偺庻柦傪帩偭偨恖娫偵傕摓払偱偒側偄柍尷偱偡丅

| NO.1486 | 2004.9.19. | 悈偺棳傟 | 俁杮偺偔偠(1) |
懢榊偝傫偼丄俶俫俲恖娫島嵗乽悢妛偺垽偟偐偨乿僺乕僞乕丒僼儔儞僋儖傪挳偄偰偄傑偡丅
偦偺拞偺僥僉僗僩偵偙傫側栤戣偑偁傝傑偡丅乽儘僩偔偠偵偼丄侾偐傜90傑偱偺悢帤偑弴偵暲傫偱偄傑偡丅
偙偺拞偐傜椬傝崌偆悢帤偑側偄傛偆偵俆屄偺悢帤傪慖傇慖傃曽側壗捠傝偁傞偱偟傚偆丅
偮傑傝慖傫偩悢帤偵嵎偑侾偵側傜側偄傛偆偵偟傑偡丅乿
偝偰丄偙偺栤戣偺夝摎傪娤偰偄偰丄師偺栤戣傪巚偄偮偒傑偟偨丅
乽値屄偺惍悢侾丆俀丆俁丆丒丒丒丄値偑彂偄偰偁傞偔偠偑偁傝傑偡丅偙偺拞偐傜俁杮偺偔偠傪堷偔偲偒丄
師偺傛偆側偔偠偺堷偔曽偼壗捠傝偁傞偐丅乮偨偩偟丄値亞俈偲偡傞乯
栤戣侾丗 俁杮偺偔偠偵彂偄偰偁傞悢帤偺偆偪丄偳偺俀偮偺悢偺嵎傕侽埲忋偲側傞応崌丅
偙偺応崌偼丄偔偠傪侾杮堷偄偨偁偲丄偙偺偔偠傪尦偵栠偟偰偔偩偝偄丅
栤戣俀丗俁杮偺偔偠偵彂偄偰偁傞悢帤偺偆偪丄偳偺俀偮偺悢偺嵎傕侾埲忋偲側傞応崌丅
栤戣俁丗俁杮偺偔偠偵彂偄偰偁傞悢帤偺偆偪丄偳偺俀偮偺悢偺嵎傕俀埲忋偲側傞応崌丅
栤戣係丗俁杮偺偔偠偵彂偄偰偁傞悢帤偺偆偪丄偳偺俀偮偺悢偺嵎傕俁埲忋偲側傞応崌丅
拲丗俶俫俲嫵堢僥儗價枅廡壩梛擔屵屻10丗25乣10丗50丂乮俉寧俁擔偐傜俋寧21擔偺俋夞乯
丂丂嵞曻憲偼枅廡壩梛擔屵慜05丗05乣05丗30丂乮俉寧10擔偐傜俋寧28擔偺俋夞乯
丂丂嵞乆曻憲偼枅廡栘梛擔屵慜02丗00乣02丗25丂乮俋寧俀擔偐傜10寧21擔偺俋夞乯

| NO.1487 | 2004.9.22. | 嶰妏掕婯 | 壜姺側峴楍偺慡懱(2) |
偙偙偱偼丆
梌偊傜傟偨幚俀師惓曽峴楍A偵懳偟丆AX亖XA丂傪傒偨偡僛儘偱側偄X偼 偁傞 p丆q 傪梡偄偰 X亖pA亄qE丂乧乧 嘆偲側偭偰偄傑偡丅
丂偟偐偟丆梕堈偵傢偐傞傛偆偵丆擟堄偺 p丆q 偵懳偟 X亖pA亄qE丂偱梌偊傜傟傞X偼丆 AX亖pA2亄qA亖XA 乧乧嘇丂傪傒偨偟傑偡丅
丂偝傜偵丆X亖O 偺偲偒 AX亖XA亖O 偲側傞偙偲偼帺柧偱嫽枴偵朢偟偄偐傜丆 X亖O 傪彍奜偟偨偔側傞婥帩偪偑傢偐傜側偔偼偁傝傑偣傫丅 偨偩丆偙偆偡傞偙偲偵傛偭偰丆A亖kE 偺偲偒 q亖亅pk 偲偡傟偽丆 X亖pA亄qE亖O丂偲側傞偺偱 A亖kE 傕彍奜偟偨偔側傞丅 乮杮栤乯
丂偟偐偟側偑傜丆媍榑偺梫偼偙傫側嵄枛側偙偲偺彍奜偱偼側偔丆
俙偲壜姺側 倃 偼 p俙亄q俤 偺宍偵尷傞偺偐丆偲偄偆偙偲偱偟傚偆丅
丂昁梫忦審偼嘇偐傜柧傜偐側偺偱丆廫暘忦審 AX亖XA 仺 X亖pA亄qE 乧乧嘊丂偑帵偝傟傟偽偄偄偺偱偡偑丆
巆擮側偑傜巹偵偼偙偺徹柧偑偱偒傑偣傫丅X亖pA亄qE 偺宍偱偼側偄偄偔偮偐偺X偑 AX亖XA 傪傒偨偝側偄偐傜偲偄偭偰丆
嘊傪徹柧偟偨偙偲偵偼側傝傑偣傫偐傜丅傕偭偲傕俀師峴楍偺応崌偵偼
yokodon 偝傫偑巜揈偝傟偰偄傞傛偆偵丆惉暘寁嶼偱嘊偑帵偝傟傞偺偱偡偑丅
丂偨偩丆栤戣偺攚宨偵偁傞偺偼埲壓偺偙偲偱偟傚偆丅A傪俀師惓曽峴楍偲偟偰
(1) 擟堄偺旕晧惍悢m偵偮偄偰丆偁偒傜偐偵丆Am亖Am丅偨偩偟丆A0亖E丅
(2) 傛偭偰丆X亖p0Am亄p1Am-1亄乧亄pm-1A亄pmE丂偲A偼壜姺丅
(3) A2亖tr(A)A亅det(A)E 乮Cayley-Hamiltom乯傪梡偄偰師悢傪壓偘丆
A偺俀師埲忋偺崁偼偡傋偰A偺侾師幃偵偱偒傞偐傜(2)偺X偼丆pA亄qE 偺宍偱昞偣傞丅
丂偙偺偙偲傪俀師埲忋偵奼挘偡傞偲丆
(1)(2)偼偦偺傑傑惉傝棫偮丅
(3) A偺屌桳曽掱幃 |A亅兩E|亖(亅1)nf(兩)亖兩n亅c1兩n-1亅乧亅cn丂偵偍偄偰 f(A)亖O (Cayley)
偑惉傝棫偮偐傜丆An亖c1An-1亄乧亄c0E丅(c1亖tr(A))
丂傛偭偰丆(2)偺A偺懡崁幃X偺師悢偑n-1師埲壓側傜偽偦偺傑傑偱丆n師埲忋側傜n-1師傑偱師悢傪壓偘傞偙偲偑偱偒丆
偦偺X偼A偲壜姺偱偁傞丅乮廫暘惈偺徹柧偼側偟乯

 E-mail
E-mail
 栠傞
栠傞