| NO.1472 | 2004.8.1. | Junko | 「よくわかる高校数学の基本と仕組み」 (1) |
秀和システムから、
「よくわかる高校数学 の基本と仕組み」という本を出版しました。
高等学校の教員として関わってきたことのエッセンスをまとめることができたかなと思っています。
是非お読みいただいた感想などいただけると嬉しく思います。

| NO.1473 | 2004.8.2. | Junko | ピーター・フランクル |
NHK
人間講座「数学の愛しかた」ピーター・フランクル
が明日から始まります。
見逃せませんね。

| NO.1474 | 2004.8.8. | 水の流れ | ニュートンの定理(1) |
太郎さんは、8月4日から6日まで開かれた全国算数・数学教育研究(鹿児島)大会に参加してきました。
高校部会では、全部で25会場に別れ延べ発表数170にもなり、暑い中盛大に行われました。
さて、その中には、次のようなレポート課題を提出させる発表がありました。
「平面幾何を勉強する中で、有名な人の名前が付いた定理を調べてきなさい。」資料の中にあった定理を書いてみます。
そこで、今回の問題はこの中にあるニュートンの定理を証明ください。解法の手段方法は問いません。1.チェバの定理とその逆
2.メネラウスの定理とその逆
3.ヒポクラテスの定理
4.アポロニウスの定理
5.ブリアンションの定理(知らなかった)
6.ニュートンの定理(知らなかった)
7.パップスの定理
8.モーレーの定理
9.デザルグの定理(知らなかった)
10.キエペルトの定理(知らなかった)
11.トレミーの定理
12.アルハゼンの定理
13.パスカルの定理
「四角形ABCDが円に外接するとき、2つの対角線の中点と円の中心は1直線上にある。」ことを証明ください。

| NO.1475 | 2004.8.27. | 松井 満 | ニュートンの定理(2) |


| NO.1476 | 2004.8.27. | DDT | ちょっとだけ数学基礎論 |
1.簡単な例
0≦a<1となる実数a全体の集合Wを考えます。明らかに、
任意の a∈W について、a<e<1となる実数e∈W が存在する. (1)
が成立ちます。何故ならこれは、a<1 の定義そのものだからです。(1)は、こういいかえてもいいはずです。
任意の a∈W について、Wに属するaの真の上界が存在する. (2)
ところで、(1)と次の(3)は、全く同じものであるはずです。
全ての a∈W について、a<e<1となる実数e∈W が存在する. (3)
(3)は、こういいかえてもいいはずです。
全ての a∈W について、Wに属するaの真の上界が存在する. (4)
(4)は、Wの全ての要素aについての性質を語っているので、次のことが成立ちそうな気がしてきます。
eをWの上界としたとき、e∈W となるものが存在する. (5)
しかし、これは不可能です。何故なら、e∈WならばWの定義より自動的にe<1となり、
やはりWの定義より自動的に、e<a<1となるa∈Wがあるからです。よって、
Wの上界は、W に属さない. (6)
が得られます。これは集合の個々の要素に対して成立つ性質が、
必ずしも要素全体を表す集合レベルでは成立しない事もある、ことを示す一例です。
2.しかし違和感がある
もう慣れてしまったから何とも思わないかもしれませんが、一歩下がって考えると、
ここには無視できない違和感があります。
それは、集合を定義する内包(性質)と、
内包から定義された外延集合の持つ性質(内包)は一致しなければならない、という当たり前の感覚です。
集合Wは、その真の上界が必ずWに属するような要素だけから構成されています。
よって、Wという、そのような要素全体の集合の上界もWに属するはずだと思ってしまうのは、
当前といえば当前な気がします。しかし成立ちません。この原因はどこにあるのでしょう?。
3.非構成的証明
1.の(1)〜(4)では、同値なことを色々と言い換えました。
ここで例えば、(1)に現れる「任意のa」について反省してみます。(1)は、
任意の a∈W について、a<e<1となる実数e∈W が存在する. (7)
です。(1)を再記した(7)の、
a∈W についてa<e<1となる実数e∈W.
の部分を、論理式Rで表し、
e が存在する.
の部分を (∃e) で表せば、(7)は、
任意の a について (∃e)R
となります。さらに
任意の a について.
の部分を (∀a) で表せば、(7)は、
(∀a)(∃e)R (8)
と書けます。ここで論理式の否定を 〜 で表すことにし、通常の (∀a) の定義に従えば、
(8)は次の(9)と同値です。
〜(∃a)(〜(∃e)R) (9)
(9)を日本語に直せば、
a<e<1となる実数e∈W を持たない a∈W は一個も存在しない. (10)
となります。(10)を素直に読めば、確かに「全ての a∈W でa<e<1となる e∈W が存在する」ことにはなります。
しかしゲーデルの完全性定理と不完全性定理があります。
以下は完全に個人的意見で、ゲーデルの2つの定理を誤解している可能性が十分にあることだけは、
あらかじめお断りしておきます。私はゲーデルの完全性および不完全性定理を、次のように解釈しました。
完全性定理従って、
枚挙可能な場合(数え尽くせる場合)には、枚挙することによって構成的証明が可能だ.
そして構成的証明が必ず正しいことは、構成的に証明できる(枚挙できるから). (11)
不完全性定理枚挙可能な場合(数え尽くせる場合)には、証明すべきケース数がいかに多かろうと、時間さえかければ必ず、 1個1個のケースを全て取り上げて構成的証明ができる。これが完全性定理です。 そこでは例えば数学的帰納法を使おうと、それは省略記法(証明のショートカット)にすぎません。 今の場合 a∈W は無限個あり、まさに枚挙不可能な場合です。 もし今の場合に数学的帰納法を使えるなら、それは単なる省略記法やショートカットではなく、 本当に数学的帰納法を用いてしか証明できない場合です。 この意味は、数学的帰納法の再帰操作を終わりまで追跡できないという意味において、 帰納法の証明は非構成的だといっています。この考えを(10)に適用してみます。
枚挙不可能な場合(数え尽くせない場合)には、非構成的証明に頼るしかない. (12)
(10)を構成的に証明するには、時間がいくらでもあると仮定して、集合Wの要素を1個1個取り出し、 (10)が成立つか否かのテストをどこまでも行えば良いわけです。でもこのテストには終わりがありません。 a が無限個あり、枚挙不可能だからです。それ故構成的証明をあきらめ、 性質 a<1 による内包的な非構成的証明を行います。 Wの全ての要素 a に対して、(10)を確認するのは実際的には不可能です。 これに対して、もしWが有限個の要素しか含まず(枚挙可能であれば)、個々の要素の性質と、 要素全体の集合の性質が一致しないなどということは絶対に起こらないはずですし、 それは個々の要素を全て取り出して構成的に証明可能です。 つまり、「集合の個々の要素に対して成立つ性質が、必ずしも要素全体を表す集合レベルでは成立しない」、 こともあるのは、無限を相手にしていたからです。ということは(10)、ひいては(10)を定義とする(8)をもって、 Wの全要素に(4)を要求することは、
(11)でもって保証された有限範囲における論理の正しさを、盲目的に無限大にまで外挿することである.(13)
ともいえます。このことから直ちに(10)が矛盾しているなどとは言いませんが、 ゲーデルの不完全性定理(12)には続きがあります。
不完全性定理だから集合論に逆理が存在しようと、それは不思議でも何でもないのです。 無限集合論は、有限範囲では完全に成立する論理を、そのことだけを頼りに、 何の保証もなく無限大に向かって外挿しただけのものです。有限の論理はいたるところで機能不全に陥ります。 自然数全体の集合と偶数全体の集合が同数である(同じ基数である)などとは、 最初聞いた時には到底信じられなかったはずです。 可算無限を全て数え尽くせるような可算無限の寿命を持つ人間がいたら、その人にとっては、 偶数全体の数は、自然数全体の個数の半分かもしれません。しかし有限である我々はそのようなテストを行えません。 ただひたすらに両集合に単射が成立することをもって(全射不成立には目をつぶり)、 自然数全体と偶数全体の数は同じと信じます。
従って、枚挙不可能な場合(数え尽くせない場合)には、非構成的証明に頼るしかない.
そして非構成的証明が必ず正しいことは、構成的には証明できない.枚挙できないから. (14)
このような事態を本気で解決しようとした果敢な日本人がいます。 ほとんど知られていませんが日戸宗太郎という人物です。彼は以上に述べたような「任意のa」に対する概念分析を行い、 「任意テスト」で成立したことを、盲目的に「全て」で成立することとして拡張することはまかりならんとして、 次の「量の制約定理」を原理におきます。
量の制約定理を提唱します。徹底的に数学概念の分析を行う彼の方法に従えば、 確かに要素と集合の性質が一致しない事も、 盲目的な無限への外挿を気づかぬうちにやってしまう事もなくなりますが、 やはり不便な(生産性の乏しい)数学でした。 ちなみに彼は、直感主義に与することもなく、現行の数学を彼の考えに従って守り抜こうとしたのですが、 残念ながら後継者は現れていません。
XとWを集合とする。X⊂W かつ W−X≠φ なら、
が成立する.ここで W−X は、WにおけるXの補集合,φは空集合を表す.
4.現行の無限集合論の普遍性
3.の真ん中あたりで、
時間がいくらでもあると仮定して、集合Wの要素を1個1個取り出し・・・
と書きました。この仮定は、物理的な現実を考慮した物理的な仮定です。
数学理論の中に物理的な仮定が紛れ込んでくるなどとは、個人的にはとんでもない異常事態だと思えます。
語弊を恐れず言ってしまえば、数学にはどうせ理屈しかないのだから、
「時間がいくらでもあると仮定して」などと言わずに、たんに「集合Wの要素を全て1個1個取り出し・・・」
と言えば済むことです。無限の時間が必要であろうと知ったことか!、です。
これが普通の数学理論の態度だと思います。ところが無限集合論だけは、この物理的仮定を取り入れました。
というか、カントルは、この仮定を受け入れざる得なかったのだと思えます。
この物理的仮定を受け入れたために、現行の無限集合論は、ある普遍性を持っているような気がします
(もちろん個人的意見です)。そしてこの普遍性は、日戸宗太郎の集合論にはなかった強さをもたらします。
我々は、こう思います。
- 任意の自然数は、有限なので枚挙可能だ。
- 可算無限以上(自然数全体の個数以上)は、有限ではないので枚挙不可能である。 時間がいくらでもあると仮定しても、それには到達できない。
さっきいった可算無限寿命人は、連続体仮説が正しかったとして、こう思います。
- 自然数全体(可算無限)は枚挙可能なので、有限だ。
- 実数全体(連続無限)は、可算だが枚挙不可能なので無限だ。時間がいくらでもあると仮定しても、 それには到達できない。
さらに一般連続体仮説が正しかったとして、連続無限寿命人は、こう思います。
- 実数全体(連続無限)は枚挙可能なので、有限だ。
- RR(1変数実数値関数全体の個数)は、可算だが枚挙不可能なので無限だ。 時間がいくらでもあると仮定しても、それには到達できない。
いいかえれば現行の無限集合論には、無限とは枚挙不可能であることだという、 無限の概念の抽象化が潜んでいます。枚挙不可能であることを認識するのは、別に我々でなくても良いのです。
可算無限寿命人にとって、自然数全体は有限であり、実数全体(我々にとっては連続無限であるもの) も可算無限にみえるかもしれません。そしてそのとき彼は、我々と同じように、 彼にとっての完全有限論理(我々にとっては可算無限で完全性を有する論理)を、 そのことだけを頼りに、何の保証もなく連続無限に向かって(彼にとっては可算無限に向かって) 外挿するかもしれません。その意味において、現行の無限集合論には、ある普遍性があるように思えます。
5.鏡映原理と無限の定義
こういうことを暗に言っていると思える人がいます。ルディー・ラッカーです。
ルディー・ラッカーの専門は無限基数で、ゲーデルともじかに討論したことのあるプロの数学者です。
彼は言います。
「枚挙可能なものとしての有限がひとたび認識されたなら、枚挙不可能なものとしての無限の概念は必然的に生じる」彼のいったことをかなり我田引水に解釈してますが、 彼はこのことを鏡映原理と呼びました。そしてもう一度いいますが、 有限とは枚挙可能(数え尽くせる)ことです。枚挙可能がどの立場でのことかは問いません。 よって無限とは、有限ではないことです。 この無意味とも思える定義が、現代数学における正式な無限の定義になります。 実際、ブルバキの数学原論集合論第2巻には、次のように書かれています。
集合が無限であるとは、それが有限でないことをいう.と。何故なら、有限であれば枚挙可能なので、無限集合論はいらないからです。 そして枚挙不可能なゆえ、無限集合は誰も見たことがありません。 そこで現在の無限集合論は力強く独断します。
無限公理! : 無限集合は存在する!.
[参考文献]
1) 数学の基礎の研究,日戸宗太郎,1967年7月,三晃堂
絶対に絶版ですが、日戸宗太郎は不遇の研究者だと思います。
2) 無限と心,ルディー・ラッカー,現代数学社,1986年5月
この本の中でルディー・ラッカーは、ゲーデルとの討論を非常に興奮して書いています。
余りにも嬉しかったのか、彼は勢い余って無限と心のエンタテイメント版であるSF小説
「ホワイトライト(ハヤカワ書房)」まで書きました。
この本は、その後に逝ったゲーデルに対する彼なりの鎮魂歌です。
蛇足ですが、彼はポップでマッドな、プロの数学ハードSF作家でもあります。
3) ブルバキ数学原論集合論第2巻,東京図書,1969年5月

| NO.1477 | 2004.8.29. | yokodon | 写像と数列 |
〜模試シリーズ19〜
自然数全体の集合から自然数全体の集合への写像 f が次の条件 (i)(ii)(iii) を
満たすものとする。但し、m, n は任意の自然数とする。
(i) f(mn) = max{f(m), f(n)}
(ii) f(n) は n の約数である。
(iii) n > 1 ならば f(n) > 1
(1)n を2以上の自然数とするとき、f(n) は n を割り切る最大の素数であること
を証明せよ。
(2)a1 を2以上の自然数とし、an+1 = an/f(an) で
数列 {an} (n = 1,2, ...) を定める。このとき、
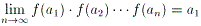
であることを示せ。

| NO.1478 | 2004.8.29. | DDT | 「よくわかる高校数学の基本と仕組み」 (2) |
今日「よくわかる高校数学の基本と仕組み」を買いました。息子に読ませようと思って最初、高校参考書の棚を探していました
(女子高生に混じって、高校参考書を手に取る親父の図)。「社会人のための再入門」だったのですね。失礼しました。
数学専門書の隣の棚の「科学一般」コーナーにありました。でも「はじめに」に「高校数学を復習したいと思っている方にも、
先取りしようと思っている方にも・・・」と書いてあったので、やっぱり息子に読ませます。
元来数学は下手の横好きで、小学,中学,高校とひたすら下降線だった私が、同輩達が既に大学卒業という時期に決行した大学受験では、
こういった準参考書(?)にずいぶんと助けられたものです。教育者にこういうことを言うと怒られそうですが、
標準的な参考書には不平・不満の塊りだったというのが本音です。数学の意味のわかる本が欲しいと、良く思いました。
ところで、同じ「科学一般」コーナーに、コロキウム室で何度か紹介した「重力と力学的世界」の著者山本義隆の最新刊が出ていました。
そこで別の本を立ち読みしてわかったのですが、山本義隆とは、東大紛争時代に全共闘の書記長をやっていたあの人で、
安田講堂の陥落を講堂側から目の当たりにした人だったのです(ご存知でしたら、すいません)。
少なくとも学問の世界からは完全に忘れ去られていた彼は、その20数年後に労作「重力と力学的世界」で、忽然と科学史界に現れます。
それまで物理学史関係で広重徹などをつまみ食いしていた私ですが、「重力と力学的世界」ほどわくわくする科学史の本を読んだ
ことがありません。前にも書きましたが、この本は、大学教養レベルの物理授業の使用に堪えるだけの内容を持ちながら、
実は数式を全て無視してもというか、むしろ数式をあえて読まないで、そこにある科学思想史を(物理の意味を)読むべきだと
思わせる本でした。その続編のような形で、再び20数年後の2003年4月に出たのが「磁力と重力の発見1,2,3、みすず書房」です。
その後書きによれば、山本義隆は科学史を現在進行形の独学でやっているとのことです。
独学は、ひたすらに効率が悪いです。この前書いた日戸宗太郎も、恐らくは数学と哲学とを独学した人で、
不遇の研究者だったのだろうと思います。山本義隆も不遇の研究者でしょうが、彼は忽然と現れられるだけの力を持っていました。
書記長はやはり、只者ではなかったようです。
独学は、ひたすらに効率が悪いです。現行の受験体制において独学に奔るのは自殺行為です。
私もいうなれば、遅れた受験勉強を独学で済ませたために、入学後は語学で惨々な目に遭いました。
でもそのおかげで、大学入試のその先には、数式や運動法則を何一つ知らなくても、これだけ面白い数学や物理の世界があるのだ、
ということも知りました(タデクウ虫も好き好きだ、ということにもなりますが)。そして数式が理解できていれば、さらに良しです。
少々強引ですが、「よくわかる高校数学の基本と仕組み」が、そのような変人共のベストセラーになることを願っています
(小島先生の本意ではないかもしれませんが)。

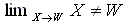
 E-mail
E-mail
 戻る
戻る