
Weekend Mathematics乛僐儘僉僂儉幒乛1998.1乣6乛NO.15
NO.107丂丂丂丂 6/1 丂丂Junko丂丂 暯曽偺栤戣乮俁乯
愇愳導棫崅壀拞妛峑
悢妛偺晹壆乽俀忔偡傞偲丒丒Part俀乿
傪撉傫偱
NO.92
偺徹柧偑姰慡偱偼側偄偙偲偑丄傢偐傝傑偟偨丅
侾偺埵偑俆偐傜巒傑傞俆丄俀俆丄俇俀俆丄丒丒丒偲偄偆宯楍偲
侾偺埵偑俇偐傜巒傑傞俇丄俈俇丄俁俈俇丄丒丒丒偲偄偆宯楍偑偁傝傑偡丅
巹偼堦斣忋偺埵傪倎乮倎亖侾丄俀丒丒丒俋乯偲偟偰丄
mod侾侽乮侾侽偱妱偭偨帪偺忚梋椶乯傪巊偭偰扵偟偰偄偒傑偟偨丅
倎亖侽傪彍奜偟偨偺偼丄椺偊偽乽侽俇俀俆乿側偳偲偄偆悢偼丄
幚嵺偵偼堄枴偑側偄偲敾抐偟偨偐傜偱偡丅
偦傟帺懱偼偄偄偲巚偆偺偱偡偑丄
偦偺抜奒偱俆偺宯楍偵偼愭偑側偄偲敾抐偟偰偟傑偭偨偙偲偼岆傝偱偟偨丅
師偺抜奒偱乽倎侽俇俀俆乿偲俆寘偱昞婰偝傟傞傕偺傪嬦枴偡傞傋偒偱偟偨丅
夵傔偰偙偙偱傗傝捈偟偰傒傑偡丅
倶俀亖(侾侽侽侽侽倎亄俇俀俆)俀 丂亖侾侽侽侽侽俀倎俀亄侾俁俆侽亊侾侽侽侽侽倎亄俁俋侽俇俀俆 丂亖(侾侽侽侽侽倎俀亄侾俁俆侽倎亄俁俋)亊侾侽侽侽侽亄俇俀俆偙傟偺侾侽侽侽侽偺埵偲倶偺侾侽侽侽侽偺埵偑堦抳偟偰偄傞偨傔偵偼丄
倶俀亖(侾侽俆倎亄俋侽俇俀俆)俀 丂亖侾侽侾侽倎俀亄侾俉侾俀俆侽亊侾侽俆倎亄俉俀侾俀俉俋侽俇俀俆 丂亖(侾侽俆倎俀亄侾俉侾俀俆侽倎亄俉俀侾俀俉)亊侾侽俆亄俋侽俇俀俆偙傟偺侾侽侽侽侽侽偺埵偲倶偺侾侽侽侽侽侽偺埵偑堦抳偟偰偄傞偨傔偵偼丄
倶俀亖(侾侽俆倎亄俋俁俈俇)俀 丂亖侾侽侾侽倎俀亄侾俉俈俆俀亊侾侽俆倎亄俉俈俋侽俋俁俈俇 丂亖(侾侽俆倎俀亄侾俉俈俆俀倎亄俉俈俋)亊侾侽俆亄俋俁俈俇偙傟偺侾侽侽侽侽侽偺埵偲倶偺侾侽侽侽侽侽偺埵偑堦抳偟偰偄傞偨傔偵偼丄
偲偙傠偱丄愇愳導棫崅壀拞妛峑偺
悢妛偺晹壆乽俀忔偡傞偲丒丒Part俀乿偺拞偱丄
峀搰導偺惔愳堢抝偝傫偑
偲偄偆晽偵婯懃惈傪巜揈側偝偭偰偄傑偡丅俆偺宯摑偵偮偄偰 丂丂丂丂丂丂丂丂俆2亖俀俆丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏俀俆 丂丂丂丂丂丂丂俀俆2亖俇俀俆丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏俇俀俆 丂丂丂丂丂丂俇俀俆2亖俁俋侽俇俀俆丏丏丏丏丏丏丏丏丏丏丏丏丏丏俋侽俇俀俆 丂丂丂丂俋侽俇俀俆2亖俉俀侾俀俉俋侽俇俀俆丏丏丏丏丏丏丏丏丏俉俋侽俇俀俆 丂丂丂俉俋侽俇俀俆2亖俈俋俁俀侾俀俉俋侽俇俀俆丏丏丏丏丏丏俀俉俋侽俇俀俆 丂丂俀俉俋侽俇俀俆2亖俉俁俆俆俈侾俀俉俋侽俇俀俆丏丏丏丏侾俀俉俋侽俇俀俆 丂侾俀俉俋侽俇俀俆2亖侾俇俇侾俇俉俀侾俀俉俋侽俇俀俆丏俀侾俀俉俋侽俇俀俆 俀侾俀俉俋侽俇俀俆2亖寘偁傆傟丅 師偵丄俇偺宯摑偵偮偄偰丄 丂丂丂丂丂丂丂丂俇2亖俁俇丏丏丏丏丏丏丏丏丏丏丏丏丏丏丏侾侽亅俁亖俈 丂丂丂丂丂丂丂俈俇2亖俆俈俈俇丅丏丏丏丏丏丏丏丏丏丏丏丏侾侽亅俈亖俁 丂丂丂丂丂丂俁俈俇2亖侾係侾俁俈俇丏丏丏丏丏丏丏丏丏丏丏侾侽亅侾亖俋 丂丂丂丂丂俋俁俈俇2亖俉俈俋侽俋俁俈俇丏丏丏丏丏丏丏丏丏侾侽亅侽亖侾侽 丂丂丂侾侽俋俁俈俇2亖侾侾俋俇俁侾侽俋俁俈俇丏丏丏丏丏丏侾侽亅俁亖俈 丂丂俈侾侽俋俁俈俇2亖俆侽俆係俁俀俀俈侾侽俋俁俈俇丏丏丏侾侽亅俀亖俉 丂俉俈侾侽俋俁俈俇2亖俈俆俉俉侽係俁俁俉俈侾侽俋俁俈俇丏侾侽亅俁亖俈 俈俉俈侾侽俋俁俈俇2亖寘偁傆傟丅
俆偺宯摑偵偮偄偰偼丄NO.92偱丄 俇俀俆傪扵偟弌偟偨帪偺偙偲傪峫偊偰傒傑偡丅
倎俀俆偲俁寘偱昞婰偱偒傞傕偺
倶亖侾侽侽倎亄俀俆
倶俀亖(侾侽侽倎亄俀俆)俀 丂亖侾侽侽侽侽倎俀亄俆侽侽侽倎亄俇俀俆 丂亖(侾侽侽倎俀亄俆侽倎亄俇)亊侾侽侽亄俀俆偙傟偺侾侽侽偺埵偲倶偺侾侽侽偺埵偑堦抳偟偰偄傞偨傔偵偼丄
俇偺宯摑偵偮偄偰偼丄NO.92偱丄 俁俈俇傪扵偟弌偟偨帪偺偙偲傪峫偊偰傒傑偡丅
倎俈俇偲俁寘偱昞婰偱偒傞傕偺
倶亖侾侽侽倎亄俈俇
倶俀亖(侾侽侽倎亄俈俇)俀 丂亖侾侽侽侽侽倎俀亄侾俆俀侽侽倎亄俆俈俈俇 丂亖(侾侽侽倎俀亄侾俆俀倎亄俆俈)亊侾侽侽亄俈俇偙傟偺侾侽侽偺埵偲倶偺侾侽侽偺埵偑堦抳偟偰偄傞偨傔偵偼丄
偝傜偵丄
侾偺埵偺悢偑俆偺偲偒傪俥値偲偡傞丅偲偄偆寢壥傪帵偟偰偄傜偭偟傖偄傑偡偑丄 偙傟偵偼姶摦偟傑偡偹丅 杮摉偵晄巚媍偱偡丅
侾偺埵偺悢偑俇偺偲偒傪俽値偲偡傞丅
俥値亄俽値亖侾侽n+1亄侾偺娭學偑傒傜傟傑偡丅

NO.108丂丂丂丂 6/1 丂丂悈偺棳傟丂丂 侾俋俋俉榓偺栤戣乮俁乯
俇寧侾擔偱僐儘僉僂儉幒偺侾擭偵側傝傑偡偹丅
偝偰丄婏悢偺応崌偼丂榓偑暯曽悢偵側傞偙偲偵婥偑偮偗偽丄
丂値俀亅倣俀亖侾俋俋俉
場悢暘夝偟偰丄
乮値亄倣乯(値亅倣乯=1998=1亊2亊3亊3亊3亊37傛傝丄
俀偮偺場悢偺榓偼俀値偲側傝丄慻傒崌傢偣偱
乮嬼悢亄婏悢亖婏悢乯偲側傞応崌偼晄壜擻偱偡丅丂丂
偟偨偑偭偰丄夝側偟丅

NO.109丂丂丂丂 6/1 丂丂Junko丂 僒亅價僗寯偺栤戣乮俀乯
摎偊偼俁俁杮偱偡偐偹丠
俁俁杮峸擖偡傞偲丄偦偺嬻偒娛傕摉慠俁俁杮偱偡偐傜丄
偦偺偆偪俁侽杮傪帩偭偰偄偗偽丄
俇杮偺娛僕儏亅僗偲岎姺偟偰傕傜偊傑偡丅
偙傟偱俁俁亄俇亖俁俋杮丅
師偵愭掱偺巆傝偺嬻偒娛俁杮偲崱夞偺嬻偒娛俇杮偱丄
崌寁俋杮暘偺嬻偒娛偑偁傞偙偲偵側傝傑偡丅
偦偺偆偪偺俆杮傪帩偭偰偄偗偽丄
娛僕儏亅僗偑侾杮傕傜偊傑偡丅
偙傟偱俁俋亄侾亖係侽杮丅
偝傜偵愭掱偺偁傑傝偺嬻偒娛係杮偲崱夞偺侾杮傪懌偟偰
崌寁俆杮暘偺嬻偒娛偑偁傞傢偗偱偡偐傜丄
偙傟偱傑偨娛僕儏亅僗侾杮偑傕傜偊偰
傔偱偨偔係侽亄侾亖係侾杮偲側傞傢偗偱偡丅
偙偺榖傪偟偨傜丄椬偺惾偺俽愭惗偑丄
乽偊亅偭丄偦傟偱偼傒傫側偱堦弿偵堸傔側偄偠傖傫丠丂
偦傫側偺偩傔偩傛亅両乿偲搟傜傟傑偟偨丅
偝傜偵丄偦傟傪暦偄偰偄偨俬愭惗丄
乽壌偺揦偵偦傫側媞偑搙乆丄嬻偒娛傪帩偭偰偒偨傜丄搟傞傛両乿
乮斵偺幚壠偼庰壆偱偡乯
乽晛捠丄僒亅價僗寯偱傕傜偭偨傕偺偵僒亅價僗寯偼偮偗側偄偱偟傚偆丒丒丒丅乿
傑偁丅偦傟偼偝偰偍偒丒丒丒丅
偦偆偦偆丄俁俀杮偱偼係侾杮傪妉摼偱偒側偄偙偲傪帵偝側偄偲偄偗傑偣傫偱偟偨偹丅
愭掱偲摨偠傛偆偵偡傟偽丄俁俋杮偟偐妉摼偱偒側偄偙偲偑傢偐傝傑偡丅
傗偭偰傒偰偔偩偝偄丅
偝偰丄偙偺傾儖僑儕僘儉傪幃偱昞偟偰傒傑偟偨丅
僈僂僗婰崋乵倶乶偲偄偆偺傪巊偄傑偡丅
偙傟偼丄倶傪墇偊側偄嵟戝偺惍悢傪梌偊傑偡丅
僀儊亅僕偲偟偰偼丄彮悢揰埲壓愗傝幪偰側偺偱偡偑丄
晧偺悢偵偮偄偰偼偙偺僀儊亅僕偩偲娫堘偊傑偡偐傜梫拲堄偱偡丅
椺
丂丂丂丂侾丏[侾丏俉俆]亖侾 丂丂丂丂俀丏[俆]亖俆 丂丂丂丂俁丏[侾侽丏俆]亖侾侽 丂丂丂丂係丏[亅俀丏俆]亖亅俁 丂丂丂丂俆丏[亅侽丏侾]亖亅侾丂
杮戣偵擖傝傑偡丅
妉摼偟偨僕儏亅僗偺杮悢傪倎値偲偟傑偡丅
偦傟傜傪偡傋偰堸傫偱丄庤帩偪偺嬻偒娛偺杮悢傪倐値偲偟傑偡丅
堦斣嵟弶偵倎杮傪峸擖偟偨偲偟傑偡丅
倎侽亖倎丄倐侽亖倎
師偺慟壔幃偱丄悢楍倎値丄倐値傪掕媊偟傑偡丅
倎値亖倎値亅侾亄乵倐値亅侾乛俆乶 倐値亖倐値亅侾亅乵倐値亅侾乛俆乶亊俆亄乵倐値亅侾乛俆乶 丂丂亖倐値亅侾亅乵倐値亅侾乛俆乶亊係倐値亙俆偱廔椆偟傑偡丅

NO.110丂丂丂丂 6/2 丂丂悈偺棳傟丂丂 係寘偺栤戣乮侾乯
慡晹偑摨偠悢帤偱偼側偄係寘偺惍悢傪
岲偒側傛偆偵慖傃側偝偄丅
偙偺係偮偺悢帤傪暲傃懼偊偰偱偒傞
嵟戝偺悢偐傜嵟彫偺悢傪堷偒丄
偦偺摎偊偱摨偠憖嶌傪孞傝曉偡丅
俁寘偺悢偵側偭偨傜1000偺埵偵侽傪偮偗傞丅
偳傫側惍悢傪慖傏偆偲嵟屻偼偁傞係寘偺悢偵側傞丅
偦偺悢偼偄偔偮偱偟傚偆偐丠
偠傖丄俁寘偺応崌偼偳傫側悢帤偵側傞偐傕峫偊偰偔偩偝偄丅

NO.111丂丂丂丂 6/2 丂丂傉乕丂丂 墌偵娭偡傞旝暘乮侾乯
1偮丄偲傫偱傕側偄偙偲乮丠乯傪偍暦偒偟偰傕椙偄偱偟傚偆偐丠
墌偺柺愊兾倰俀傪旝暘偡傞偲
墌廃偺俀兾倰偵側傝丄
摨偠偔媴偺懱愊係乛俁兾倰俁傪旝暘偡傞偲
昞柺愊偺係兾倰俀偵側傞偺偼側偤偱偟傚偆偐丠

NO.112丂丂丂丂 6/2 丂丂悈偺棳傟丂丂 僒亅價僗寯偺栤戣乮俁乯
僒乕價僗寯偺栤戣偼俁俁杮偱丄嬻偒娛偑侾杮巆傝傑偡丅
幚偼丄弴偵堸傒姳偟帪娫偑昁梫偱偡偺偱丄
俁夞懸偮偙偲偵側傝傑偡丅
偦偙傪揦偺恖偵棟夝偟偰傕傜偄堦搙偵峸擖偡傞偙偲偑
偱偒傞偲椙偄偺偱偡偑丅
偱傕丄俀侾悽婭偺嬤偄彨棃儕僒僀僋儖偱丄
偙偺傛偆側僒乕價僗寯偑敪峴偝傟傞偐傕偟傟傑偣傫丅
愭庢傝妛廗偺偮傕傝偱峫偊傑偟傚偆丅
偝偰丄僐儘僉僂儉幒偺拞偱丄
妉摼偟偨僕儏乕僗偺杮悢傪倎(n),
庤帩偪偺嬻偒娛偺杮悢傪倐(n)偲偡傞丅
堦斒偵丄乮倠偼帺慠悢乯
丂倎(n)亖係倠亄倣乮倣亖1丆2丆3丆4乯偺偲偒丄
丂倐(n)亖俆倠亄倣偲側傝丄倠杮僒乕價僗偵側傝傑偡丅
丂偝傜偵丄倣杮嬻偒娛偲偟偰巆傝丄岎姺偼師夞偵側傝傑偡丅
榖偼傛偔帡偰偄傑偡偑丅
偁傞偲偒丄戝僶乕僎儞僙乕儖偱丄50亾倧倖倖丂
巆傝偺50亾偼彜昳寯傪偝偟忋偘傑偡丅
彯丄偙偺彜昳寯偼偙偺婜娫拞偵彜昳偵岎姺偱偒傞応崌
偲偦偆偱側偄応崌傪峫偊傞偲丄杮摉偵敿妟側偺偱偟傚偆偐丠
峫偊傕偺偱偡丅

NO.113丂丂丂丂 6/4 丂丂悈偺棳傟丂丂 墌偵娭偡傞旝暘乮俀乯
墌偺旝暘偵偮偄偰丄巹偺庼嬈晽宨傪徯夘偟傑偡丅
丂
暯柺忋偺柺愊偵偮偄偰丄嬫娫乵倎丆倐乶偱丄
倖(x)亞侽偲偡傞丅
嬋慄丂倷亖倖(x) 偲倶幉丄偍傛傃俀捈慄倶亖倎丆倶亖倐丂
偱埻傑傟偨晹暘偺柺愊俽偼
俽亖佺(x=a乧x=b) 倖(x) dx 丂偱昞偝傟傑偡丅
幚偼丄嬫娫乵倎丆倐乶偱丄擟堄偺倶偺抣偵懳偟偰
偙偺倖(x)偼堦杮偺慄暘偺挿偝傪帵偟偰偄傞偲峫偊偰偔偩偝偄丅
偙偺堦杮堦杮偺捈慄傪嬫娫乵倎丆倐乶傑偱婑偣廤傔偰偱偒偨偺偑丄
媮傔傞埻傑傟偨晹暘偺柺愊偲峫偊傑偡丅
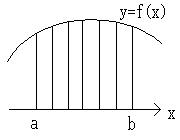
巹偺応崌丄偙偺強偺庼嬈偼壓偵悅傟壓偑偭偨桪夒側嬋慄傪
昤偄偨憰忺梡乽偡偩傟乿傪嫵嬶偵偟傑偡丅
憐憸偱偒傑偟偨偐丅
乮側偄偲偒偼丄夋梡巻傪偼偝傒偱揔摉偵愗偭偰丄
懄惾偺乽偡偩傟乿傪嶌傝傑偡丅乯
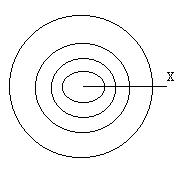
偝偰丄敿宎倰偺墌偵偮偄偰丄偦偺拞偵摨怱墌傪嶌傝傑偡丅
拞怱傪尨揰偵偲傝丄恾偺傛偆偵倶幉傪庢傝傑偡丅
偙偙偱丄偙偺墌傪庽栘偺擭椫偺傛偆偵昞旂傪堦枃堦枃偼偑偟偰偄偒傑偡丅
乮巕嫙偺僶乕儉僋乕僿儞偺怘傋曽傪巚偄弌偟偰偹丅乯
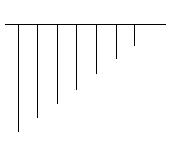 偦傟傪壓偵堦杮堦杮廲偵暲傋偰偔偩偝偄丅
偦傟傪壓偵堦杮堦杮廲偵暲傋偰偔偩偝偄丅
偡傞偲丄堦斣嵍偺慄偺挿偝偼俀兾倰偱
偙偺墶偼敿宎偺倰偱偡丅
偩偐傜丄墌偺柺愊偼 俀兾倰亊倰亐俀亖兾倰俀
乮敿宎倰偺墌偺墌廃偑俀兾倰偱偁傞偙偲偼婛抦偲偟傑偡乯
偙偺偙偲傪愭傎偳偺丄愊暘偱峫偊傞偲丄
嬫娫乵侽丆倰乶偺擟堄偺倶偵懳偟偰丄
慄暘偺挿偝俀兾倶 傪婑偣崌傢偣傞偲丄
兾倰俀亖佺(x=0乧x=r)俀兾x dx
亙巹偼偙偺傛偆側曽朄偱愗偭偰丄愊暘偡傞偙偲傪塓姫偒愊暘丒
擭椫愊暘偲惗搆偵偼尵偭偰偄傑偡丅亜
幙栤偺摎偊偲偟偰偼丄墌偺柺愊傪旝暘偡傞偲丄
墌廃偵側傞偲峫偊傞偺偱側偔丄
墌廃偺挿偝俀兾x 傪侽偐傜倰傑偱愊暘偡傞偲丄
墌偺柺愊傪昞偡偺偱偡丅
師偼丄媴偺懱愊偵堏傝傑偡丅
偙傟傕丄庼嬈偱偼僞儅僱僊偺昞旂傪堦枃堦枃偼偑偟偰丄
惗搆偵偼愢柧偟傑偡丅
乮廘偄偼憡摉側傕偺偑偁傝傑偡丒丒丒偡偖偵偐偨偢偗傞偙偲乯
媴偺昞柺愊偑係兾倰俀 偱偁傞偙偲偼丄
惗搆偵偼傒偐傫偺旂偱愢柧偟傑偡丅
乮側偄偲偒偼丄巻晽慏傪巊偄傑偡丅
偩偐傜丄偲偒偳偒栻嬊偱傕傜偆応崌戝愗偵曐娗偟偰偁傝傑偡丅
攋偭偰巊偆偨傔擇搙偲暅尦偟傑偣傫丅乯
敿宎倰偼應偭偰抦偭偰偍偄偰偔偩偝偄丅
側傞傋偔娵偄傒偐傫傪敿暘偵愗偭偰旂傪偼偑偟傑偡丅
揔摉側戝偒偝偵偟偰丄
敿宎俀倰偺墌偺昞柺偵挘傝晅偗偰偔偩偝偄丅
堦晹岆嵎偼偁傝傑偡偑丄堦柺偵挘傝晅偗傜傟傑偡丅
乮愭傎偳偺巻晽慏偺応崌偼媡偵偺傝偟傠偺晹暘傪偼偑偟偰偄偗偽傛偄偺偱偡丅
偼偑偟曽偵尋媶偺梋抧偑偁傝傑偡丅
嵟屻偼忋庤偵墌偵挘傝晅偗偰偹丅乯丂丂徹柧廔傢傝
嬻娫偱偺懱愊偺媮傔曽偼丄倶幉傪峫偊丄
偦傟偵悅捈側暯柺偵傛傞棫懱偺愗傝岥偺柺愊傪俽(x)偲偡傞丅
嬫娫倎亝倶亝倐偺斖埻偵偁傞棫懱偺懱愊偼
倁亖佺(x=a乧x=b) 俽(x) dx 丂 偱昞偝傟傑偡丅
懱愊偺媮傔曽偼偄偐偵偟偰丄棫懱傪愗偭偰偄偔偺偐丅
傑偨偼丄偼偑偟偰偄偔偺偐偱偡丅
偙偺扨尦偱偺嫵嬶偼丄偝偮傑偄傕偐億僥僩偲
巗斕偝傟偰偄傞摏偺億僥僩僠僢僾僗傪弨旛偟傑偡丅
偝偮傑偄傕偐億僥僩傪傑側斅偺忋偱愗偭偰僗儔僀僗偟偨
僠僢僾僗傪婑偣廤傔偨棫懱偺懱愊偑忋偺岞幃偵側偭偰偄傑偡丅
乮巹偺応崌暿柤僗儔僀僗愊暘偲尵偄傑偡丅乯
丂偱偼丄側傞傋偔娵偄僞儅僱僊偺旂傪堦枃堦枃傓偄偰丄
偦傟傪婑偣廤傔偰丄偐傇偣偰偄偒傑偡丅
乮戝偒偝偺堘偆朮巕傪巚偄弌偟偰廳偹偰偔偩偝偄丅乯
媴偑弌棃傑偡丅
媴偺懱愊亖乮堦枃堦枃偺昞柺愊乯亊乮岤傒乯
亖 佺(x=0乧x=r)係兾倶俀 dx
乮偙偺柦柤偼昞旂愊暘丄愥偩傞傑愊暘丄
僐乕儞愊暘偲尵偭偰偄傑偡丅乯偝偰丄偄傠偄傠側柤慜偺愊暘偑偱偰偒傑偟偨偹丅
懠偵僶乕儉僋乕僿儞愊暘傪揱偊傑偡丅
夞揮懱偺懱愊傪媮傔傞偺偵棙梡偟傑偡丅
侽亝倎亝倶亝倐 偵偍偄偰丄嬋慄倷亖倖(x)亞侽丂偲
倃幉偲偺椞堟傪倄幉偺廃傝偵夞揮偟偰偱偒傞棫懱偺懱愊傪倁偲偡傞丅
乮梞壻巕偺僶亅儉僋亅僿儞傪巚偄弌偟偰偔偩偝偄丅乯
亙倄幉偺廃傝偵夞揮偟偨棫懱偺懱愊偱偡亜
偱偼丄偙偺棫懱偺昞旂傪戝崻偺宩傓偒傛偆偵偼偑偟傑偡丅
乮嫵幒偵偼戝崻偑偁傝丄巹偑曪挌偱旂傪傓偄偰偄傑偡丅
偍偐偘偱丄宩傓偒偼摼堄偵側傝偦偆偱偡丅乯
倎亝倶亝倐 偺擟堄偺倶偵懳偟偰丄
尨揰偐傜倶偺嫍棧偵偁傞堦枃偺昞旂偺敿宎偼倶偩偐傜丄
墌廃偼俀兾倶偱丄崅偝偑倖(x)偵側傝傑偡丅
偙偺昞旂偺柺愊偼俀兾倶倖(x) 偲側傝丄
倁亖佺(x=a乧x=b)俀兾倶倖(x) dx 偲偄偆岞幃偑惗傑傟傑偡丅

NO.114丂丂丂丂 6/4 丂丂悈偺棳傟丂丂 墌偵娭偡傞旝暘乮俁乯
敿宎10噋偺俀偮偺捈墌拰傪捈岎偝偣偨偲偒丄岎傢傝偺晹暘偺懱愊傪媮傔偰偔偩偝偄丅
乮偳偺傛偆偵僗儔僀僗偡傞偐偑億僀儞僩偱偡丅乯

NO.115丂丂丂丂 6/4 丂丂悈偺棳傟丂丂 墌偵娭偡傞旝暘乮係乯
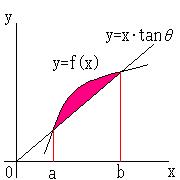
嬋慄俠丗倷亖倖(x)偲捈慄倣丗倷亖倶tan兤 偱埻傑傟偨恾宍傪丄
捈慄 倣 傪 幉偲偟偰夞揮偟偰摼傜傟傞棫懱偺懱愊倁傪媮傔傛丅
乮栜榑丄埻傑傟偨恾宍偑偁傞応崌乯

NO.116丂丂丂丂 6/4 丂丂Junko丂丂 墌偵娭偡傞旝暘乮俆乯
巹傕偙偺帠幚傪抦偭偨偲偒丄姶摦偟傑偟偨丅
偦偺棟桼傪帺暘側傝偵擺摼偱偒偨帪偵偼丄
旝暘朄偺偡偛偝傪幚姶偟偨偺傪妎偊偰偄傑偡丅
旝愊暘偼尩枾偵傗傠偆偲偡傞偲偲偰傕戝曄側偺偱丄
乮棟壢宯偺妛惗偺懡偔偼丄
戝妛侾擭惗偱兠亅兟榑朄偵擸傑偝傟傞偼傔偵側傝傑偡丅乯
姶妎揑側榖傪偟傑偡丅
杮戣偵擖傞慜偵丄傑偢柺愊偺榖傪偟傑偡丅
崅峑俀擭惗偺庼嬈偱丄娭悢傪掕愊暘偡傞偲柺愊偑弌傞傛偲偄偆偁傟偱偡丅
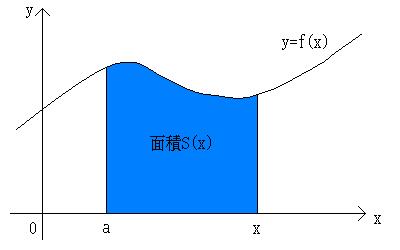
娭悢倷亖倖(倶)偺僌儔僼乮偙偺斖埻偱偼倷亜侽偲偟偰峫偊傑偡丅乯偲丄
捈慄倷亖倎乮倎偼掕悢乯偲捈慄倶亖倶丄
偦偟偰倶幉偺係偮偱埻傑傟偨晹暘偺柺愊傪峫偊傞偲
偙傟偼倶偺娭悢偵側傞偺偱丄俽(倶)偲偟傑偡丅
俽'(倶)亖倖(倶)丄偮傑傝柺愊偺娭悢俽(倶)傪旝暘偡傞偲傕偲偺娭悢倖(倶乯偵側傞丅
偩偐傜柺愊傪媮傔偨偄帪偼旝暘偺媡丄偮傑傝愊暘傪偡傟偽偄偄偲偄偆偙偲偵側傞傢偗偱偡丅
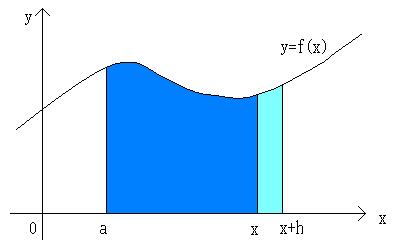
摫娭悢偺掕媊傛傝丄
俽'(倶)亖lim(h仺0){俽(倶亄倛)亅俽(倶)}乛倛
偙偙偱丄俽(倶亄倛)亅俽(倶)偺恾宍揑堄枴傪峫偊傞偲丄
嵍偺恾偺悈怓偺晹暘偵側傝傑偡丅
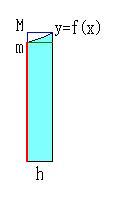
偙偺斖埻丄倶乣倶亄倛偱偺倖(倶乯偺嵟戝抣傪俵丄嵟彫抣傪倣偲偡傞側傜偽丄
柺愊偺娭學偐傜師偺晄摍幃偑惉傝棫偪傑偡丅
倣倛亙俽(倶亄倛)亅俽(倶)亙俵倛
偙傟傜傪倛亜侽偱傢傞偲丄
倣亙{俽(倶亄倛)亅俽(倶)}乛倛亙俵丂偲側傝傑偡丅
h仺0偺嬌尷傪峫偊偨偲偒偵丄倣傕俵傕嵍抂偺抣丄
偮傑傝倖(倶乯偵嬤偯偔偙偲偐傜丄
俽'(倶)亖lim(h仺0){俽(倶亄倛)亅俽(倶)}乛倛亖倖(倶)
偑尵偊傞傢偗偱偡丅
幚偵姶妎揑側榖傪偡傞偲丄旝暘偲偄偆偺偼丄
彮偟暆(倛)傪帩偨偣偰偍偄偰丄
偦偺暆傪尷傝側偔侽偵嬤偯偗偨帪偵偳偆側傞偐偲偄偆榖偱偡丅
偱偡偐傜丄柺愊傪旝暘偡傞偲忋偺恾偺愒偄儔僀儞偵側傞偺偱偡丅
傑偨丄愊暘偲偄偆偺偼楢懕揑偵懌偟偰偄偔偺偩偲偄偆姶妎偱榖傪偡傞側傜偽丄
愒偄儔僀儞傪彊乆偵懌偟偰偄偔偲丄柺愊偵側傞偲偄偆傢偗偱偡丅
乮捈慄偵偼暆偑側偔丄偦傟傪偄偔傜懌偟偰傕柺愊偼侽偩偲尵傢傟偦偆偱偡偑丄
偦偙偼偛姩曎丅嬌傔偰姶妎揑偵榖傪偟偰偄傑偡偺偱丒丒丒丅乯
偝偰丄墌偺榖傪偟傑偟傚偆丅
敿宎倰偺墌偺柺愊傪俽(倰)偲偟傑偟傚偆丅
俽(倰)亖兾倰俀偼傛偔偛懚偠偱偡傛偹丅
偙傟傪旝暘偡傞偲丄俽'(倰)亖俀兾倰偲側傝丄偙傟偼奜廃偺挿偝偱偡丅
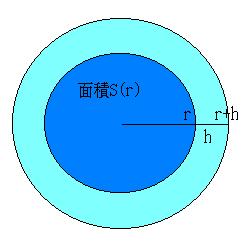
愭掱偲摨偠傛偆偵峫偊傞偲丄
摫娭悢偺掕媊傛傝丄
俽'(倰)亖lim(h仺0){俽(倰亄倛)亅俽(倰)}乛倛
偙偙偱丄俽(倰亄倛)亅俽(倰)偺恾宍揑堄枴傪峫偊傞偲丄
嵍偺恾偺悈怓偺晹暘偵側傝傑偡丅
偙偺僪亅僫僣晹暘偺柺愊偼丄
奜懁偺奜廃偺挿偝傪侾曈偲偟丄
傕偆侾曈傪倛偲偡傞挿曽宍傛傝偼彫偝偄偗傟偳丄
撪懁偺奜廃偺挿偝傪侾曈偲偟丄
傕偆侾曈傪倛偲偡傞挿曽宍傛傝偼戝偒偄傢偗偱偡丅
偱偡偐傜丄師偺晄摍幃偑惉傝棫偪傑偡丅
俀兾倰倛亙俽(倰亄倛)亅俽(倰)亙俀兾(倰亄倛)倛
偙傟傜傪倛亜侽偱傢傞偲丄
俀兾倰亙{俽(倰亄倛)亅俽(倰)}乛倛亙俀兾(倰亄倛)
h仺0偺嬌尷傪峫偊偨偲偒偵丄
奜懁偺敿宎傕倰偵嬤偯偔傢偗偱偡偐傜丄
俽'(倰)亖lim(h仺0){俽(倰亄倛)亅俽(倰)}乛倛亖俀兾倰
偑尵偊傞傢偗偱偡丅
愭掱偲摨偠偵姶妎揑側榖傪偡傞偲丄 墌偺柺愊丄倰傪傎傫偺彮偟(倛)憹傗偟偰丄 偦偺暆(倛)傪尷傝側偔侽偵嬤偢偗傞偲墌廃偺挿偝偵側傞偺偱偡丅
愊暘偱傒傟偽丄墌偺敿宎倰傪彮偟偢偮憹傗偟側偑傜丄
墌廃偺挿偝傪懌偟偰偄偔偲柺愊偵側傞偺偱偡丅
媴偺懱愊偵偮偄偰傕丄摨偠傛偆偵愢柧偱偒傞偲巚偄傑偡丅
敿宎倰偺媴偺懱愊傪倁(倰)偲偡傞偲丄
倁(倰)亖(係乛俁)兾倰俁
偙傟傪旝暘偡傞偲丄
倁'(倰)亖係兾倰俀偲側傝丄
偙傟偼敿宎倰偺媴偺昞柺愊傪梌偊傞幃偲側傝傑偡丅
旝暘偱峫偊傞偲丄媴偺懱愊丄倰傪傎傫偺彮偟(倛)憹傗偟偰丄 偦偺暆(倛)傪尷傝側偔侽偵嬤偢偗傞偲昞柺愊偵側傞偺偱偡丅
愊暘偱尵偊偽丄墌偺敿宎倰傪彮偟偢偮憹傗偟側偑傜丄
昞柺愊傪懌偟偰偄偔偲懱愊偵側傞偺偱偡丅

NO.117丂丂丂丂 6/5 丂丂償傽乕丂丂丂 墌偵娭偡傞旝暘乮俇乯
乽墌偵娭偡傞旝暘乿偵懳偡傞堄尒偱偡偑丄
偙偺峫偊曽偼偄傠偄傠側恾宍偵墳梡偱偒傑偡偹丅
偙偙偱偼椺偲偟偰丄
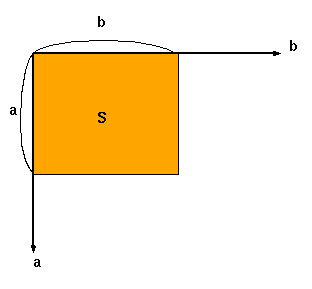
(1)挿曽宍
|
偨偰乽a乿墶乽b乿偺挿曽宍偺柺愊乽S乿偼 S=ab 偱偡丅 塃偺恾偺傛偆偵嵗昗幉乽a乿乽b乿傪庢偭偰偍偔偲旝暘偡傞偲尵偆堄枴偑傢偐傝傗偡偄偲巚偄傑偡丅 |
|
|
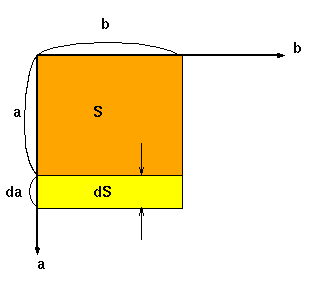
偙偺S傪乽a偺娭悢乿偩偲巚偭偰乽a偱旝暘乿偡傞偲丄 dS/da = b
偲側傝丄偙傟偼墶偺挿偝傪昞偟傑偡丅 |
|
|
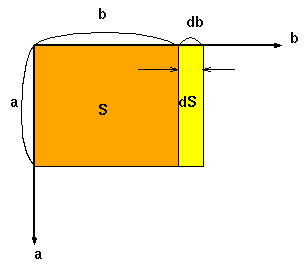
傑偨S傪乽b偺娭悢乿偩偲巚偭偰乽b偱旝暘乿偡傞偲丄 dS/db = a
偲側傝丄偙傟偼廲偺挿偝傪昞偟傑偡丅 |
|
|
掙柺偺墌偺敿宎乽r乿丄崅偝乽h乿偺墌拰偺懱愊乽V乿偼 V=兾r2h 偱偡丅 h幉偲r幉偼塃偺恾偺傛偆偵庢偭偰偍偒傑偟傚偆丅 |
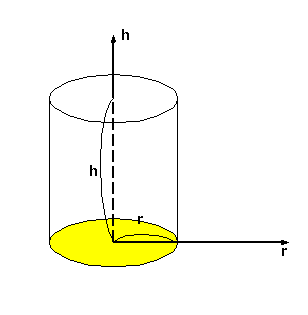
|
|
偙偺懱愊傪乽r偺娭悢乿偩偲巚偭偰乽r偱旝暘乿偡傞偲丄 dV/dr = 2兾rh
偲側傝丄偙傟偼墌拰偺懁柺愊傪昞偟傑偡丅 |
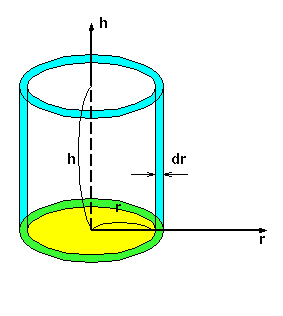
|
|
傑偨V傪乽h偺娭悢乿偩偲巚偭偰乽h偱旝暘乿偡傞偲丄 dV/dh = 兾r2
偲側傝丄偙傟偼墌拰偺掙柺愊傪昞偟傑偡丅 |
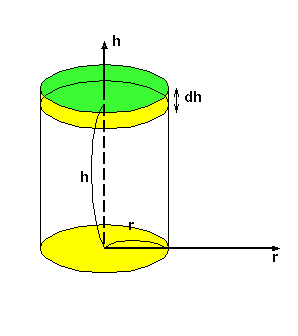
|
|
掙柺愊乽S乿丄崅偝乽h乿偺墌偡偄偺懱愊乽V乿偼 V= Sh/3
偱偡丅 dV/dh = S/3
偵側傝傑偡丅 |
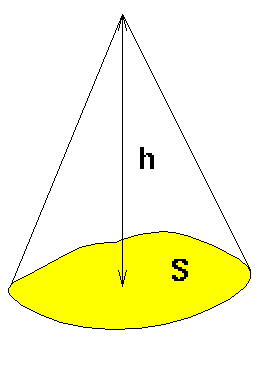
|

NO.118丂丂丂丂 6/6 丂丂Junko丂丂 係寘偺栤戣乮俀乯
俁寘偵偮偄偰偼丄偄傠偄傠傗偭偰傒傞偲昁偢嵟屻偼乽係俋俆乿偵
偨偳傝偮偔傛偆偱偡丅偙傟傪帵偟傑偡丅
俁寘偺悢帤傪戝偒偄弴偵暲傋懼偊偨忬懺偱乽倎倐們乿偲昞婰偝傟偰偄偨偲偟傑偡丅
乮倎亞倐亞們丄偨偩偟倎亖倐亖們偼彍偔乯
丂乽倎倐們乿亅乽們倐倎乿 亖(侾侽侽倎亄侾侽倐亄們)亅(侾侽侽們亄侾侽倐亄倎) 亖俋俋(倎亅們)偙偙偱丄倎亅們亖倠偲偍偔偲丄
丂乽俋(俋亅倠)倠乿亅乽倠(俋亅倠)俋乿
亖{俋侽侽亄侾侽(俋亅倠)亄倠}亅{侾侽侽倠亄侾侽(俋亅倠)亄俋}
亖俋俋(俋亅倠)
倠亖侽丆侾丆俀丆俁丆係偱偡偐傜丄嬶懱揑偵偼丄
丂乽俋(俋亅倢)倢乿亅乽倢(俋亅倢)俋乿
亖{俋侽侽亄侾侽(俋亅倢)亄倢}亅{侾侽侽倢亄侾侽(俋亅倢)亄俋}
亖俋俋(俋亅倢)
倢亖侾丆俀丆俁丆係偱偡偐傜丄嬶懱揑偵偼丄
丂乽俋(俋亅倣)倣乿亅乽倣(俋亅倣)俋乿
亖{俋侽侽亄侾侽(俋亅倣)亄倣}亅{侾侽侽倣亄侾侽(俋亅倣)亄俋}
亖俋俋(俋亅倣)
倣亖俀丆俁丆係偱偡偐傜丄嬶懱揑偵偼丄
丂乽俋(俋亅値)値乿亅乽値(俋亅値)俋乿
亖{俋侽侽亄侾侽(俋亅値)亄値}亅{侾侽侽値亄侾侽(俋亅値)亄俋}
亖俋俋(俋亅値)
値亖俁丆係偱偡偐傜丄嬶懱揑偵偼丄
丂俋俆係亅係俆俋 亖係俆俋偲側傝丄偨偐偩偐俇夞偺憖嶌偱偡傋偰乽係俆俋乿偵婣拝偟傑偡丅
俀寘偵偮偄偰偼丄嵟屻偼僒僀僋儕僢僋偵側傞傛偆偱偡丅
偙傟傪帵偟傑偡丅
俀寘偺悢帤傪戝偒偄弴偵暲傋懼偊偨忬懺偱乽倎倐乿偲昞婰偝傟偰偄偨偲偟傑偡丅
乮倎亜倐乯
丂乽倎倐乿亅乽倐倎乿 亖(侾侽倎亄倐)亅(侾侽倐亄倎) 亖俋(倎亅倐)偙偙偱丄倎亅倐亖倠偲偍偔偲丄
丂乽(俋亅倠)倠乿亅乽倠(俋亅倠)乿
亖{侾侽(俋亅倠)亄倠}亅{侾侽倠亄(俋亅倠)}
亖俋(俋亅俀倠)
俋亅俀倠亖倢偲抲偒捈偡偲丄倠亖侽丆侾丆俀丆俁丆係傛傝丄
倢亖俋丆俈丆俆丆俁丆侾偲側傝丄嬶懱揑偵偼
係寘偵偮偄偰偼丄俇侾俈係偵婣拝偟丄
僇僾儕僇悢偲偄偆偺偩偦偆偱偡偑丄傛偔傢偐傝傑偣傫丅

 栠傞
栠傞