| NO.1446 | 2004.2.1. | 水の流れ | 長方形(1) |
現在太郎さんは平面幾何を教えています。平面幾何の問題は多様なアプローチが可能です。
ここで、問題です。
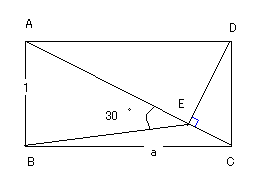
長方形ABCDにおいて、頂点Dから、対角線ACに引いた垂線の足をEとすると、
∠AEB=30゜である。AB=1として、BC=a を求めよ。

| NO.1447 | 2004.2.4. | Junko | 長方形(2) |
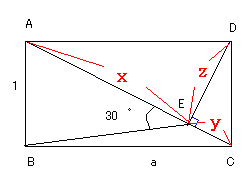
AE=x,EC=y,DE=zとする。
ピタゴラスの定理により、x+y=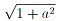
△AED、△DEC、△ADCは相似の関係にあることから、
x:z=a:1 x=az
z:y=a:1 y=(1/a)z
これより、
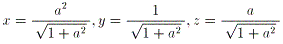
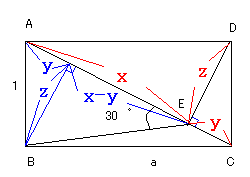
一方、△ABEに注目すると、∠AEB=30°であることから,
x-y:z = 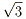 :1
:1
①を代入することにより、a2-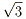 a-1=0
a-1=0
a>0より、
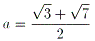

| NO.1448 | 2004.2.12. | 小学名探偵 | ランダムウォークに関する問題(1) |
(問題):一次元のランダムウォークに関して、
2N歩目(Nは正整数)を含んでそれまでに一度も元の位置を経ることがない
経路の集合と2N歩目に元の位置にいる経路の集合が1対1で対応していることを
示してください。

| NO.1449 | 2004.2.12. | 本多欣亮 | 作図ソフト「シンデレラ」 |
作図ソフト、シンデレラの紹介です。
書店で偶然見かけたソフトを紹介します。名前を「シンデレラ」という、作図の
ためのソフトです。多数のOSで動作し、様々な出力ファイル形式に対応しており
ます。また、点と線分の交叉判定などに独自のアルゴリズムを採用し、単なる作
図だけでない幅広い図形分析・編集ソフトに仕上がっているようです。小中学生
の教員・塾家庭教師などに最適かもしれませんね。

| NO.1450 | 2004.2.13. | 小学名探偵 | 条件を満たす多項式の個数(2) |
(コロキウム室の問題NO.1434に対するヒント)
(1) とりあえず、次数zの低いほうから調べていけば規則性が見えてくると思います。
(2) z次において、
不等式条件:
nz <F(z) < (n+1)z
を満たすz次多項式(適合多項式)の完全なセットS(F(z))を、
S(F(z))≡{(n+2)a*(n+1)b*(n)c, (n+1)a*nb*(n-1)c}
で表すことにします(z=a+b+c : a, b, c, は非負の整数)。
適合多項式が、3以上の正整数sについて、(n+s)の因数(ターム)を持つことはあり得ません。
理由は任意の非負の整数kについて
(n+3)(n+1)k> (n+1)k+1
になるからです。
同様の理由( nk*(n-2) < nk+1 )で、適合多項式が、
(n-s+1)の因数(ターム)を持つことはあり得ません。
もう少し、適合多項式F(z)の形式を具体化しますと、a, b, cを改めて正整数と読み替えて、
適合多項式F(z)は:
(n+2)a の形式にはなり得ません。
(n+1)b の形式にはなり得ません。
nc の形式にはなり得ません。
(n+2)a*(n+1)b の形式にはなり得ません。
( (n+2)a*(n+1)b> (n+1)a+b )
(n+2)a*nc の形式には条件次第でなり得ます。
(n+2)a*(n+1)b*nc の形式には条件次第でなり得ます。
(n+1)b*nc の形式は無条件でOKです。
すなわち、 (n+1)b*ncはS(F(z))の要素です。
(n-1)c の形式にはなり得ません。
(n)b*(n-1)c の形式にはなり得ません。
(n+1)a*(n-1)c の形式には条件次第でなり得ます。
(n+1)a*nb*(n-1)c の形式には条件次第でなり得ます。
(3) n >=(z+1)/2 の場合と、n =(z-1)/2の場合に分けて考えてみてはいかがでしょうか。

| NO.1451 | 2004.2.18. | 小学名探偵 | 積の和の問題(1) |
11×12×13×14 + 12×13×14×15 + 13×14×15×16 +・・・+ 99×100×101×102
の合計はいくつでしょうか。2つの積の差で求められます。そうなる理由も説明してください。

| NO.1452 | 2004.2.25. | 水の流れ | 正n面体 |
太郎さんは今まで考えていなかったことがあります。
それは3次元空間では正n面体といわれているものは
n=4,6,8,12、20の5個があります。それでは、このほかにあるのでしょうか、
それとも5個の限るのでしょうか、考えてみます。最初に、オイラーの多面体定理を示します。
「1つの多面体の頂点の個数をV、辺(稜または線)の個数をE 、面の個数をFとすると、
V-E+F=2 が成り立つ。
各正多面体の頂点・辺・面の個数を書き上げてみると、次の表のようになる。
| V | E | F | V-E+F | |
|---|---|---|---|---|
| 正4面体 | 4 | 6 | 4 | 2 |
| 正6面体 | 8 | 12 | 6 | 2 |
| 正8面体 | 6 | 12 | 8 | 2 |
| 正12面体 | 20 | 30 | 12 | 2 |
| 正20面体 | 12 | 30 | 20 | 2 |
次に、必要な事実があります。
「事実1」:1つの頂点に集まる面の数は3以上である。
「事実2」:1つの頂点に集まる角の大きさは、360゜未満である。
ここで、問題です。3次元空間では正n面体は何種類あるでしょうか。

| NO.1453 | 2004.2.27. | UnderBird | 積の和の問題(2) |
| n(n+1)(n+2)(n+3) | |
| = | {n(n+1)(n+2)(n+3)(n+4)-(n-1)n(n+1)(n+2)(n+3)}/5 |
であるから、
| 11×12×13×14 + 12×13×14×15 + 13×14×15×16 +・・・+ 99×100×101×102 | |
| = | { 11×12×13×14×15 - 10×11×12×13×14 +12×13×14×15×16 - 11×12×13×14×15 +13×14×15×16×17 - 12×13×14×15×16 + ・・・ - ・・・ +99×100×101×102×103 - 98×99×100×101×102 }/5 |
| = | ( 99×100×101×102×103 - 10×11×12×13×14 )/5 |
| = | ( 10504949400 - 240240 )/5 |
| = | 2100941832 |

 E-mail
E-mail
 戻る
戻る